Особенности нестационарных тепловых процессов в одномерных гармонических кристаллах

Введение

В настоящее время изучение нелинейных термомеханических процессов в низкоразмерных структурах привлекает особое внимание в связи с бурным развитием наноэлектронных устройств разработанных на основе материалов с микроструктурой . Достижения в области нанотехнологий позволили экспериментально подтвердить волновую природу теплопередачи и конечную скорость распространения тепловых возмущений . Результаты исследований подобных явлений могут послужить основой для создания универсальной теории теплопроводности, применимой как на микро-, так и на макромасштабах.

В данной работе мы выбрали для рассмотрения тепловых процессов одну из простейших систем: однородную одномерную среду, в которой отсутствуют механические движения. В этом случае уравнение баланса энергии может быть записано в виде Вывод уравнения будет дан ниже: –. В упрощенной формулировке не учтен объемный подвод тепла.[math]U = -h’[/math], где [math]\rho[/math] — плотность среды, [math]U[/math] — внутренняя (в данном случае чисто тепловая) энергия, [math]h[/math] — тепловой поток, точкой обозначена производная по времени, штрихом — по координате. Так как в рассматриваемом случае изменение тепловой энергии связано только с изменением температуры, то [math]U = c_V T [/math],где [math]T[/math] — температура, [math]c_V[/math] — теплоемкость при постоянном объеме. Если изменения температуры невелики, то теплоемкость можно считать постоянной величиной. Связь теплового потока с температурой обычно описывается законом Фурье : [math]h = -T’ T = T”[/math] — в результате мы получили классическое уравнение теплопроводности, где [math]\kappa[/math] — коэффициент теплопроводности, [math]{\beta = \kappa/(\rho c_V)}[/math] — коэффициент температуропроводности, точка [math]\dot{(~~)}[/math] обозначает дифференцирование по времени [math]t[/math], штрих [math](~~)'[/math] дифференцирование по координате [math]x[/math]. Уравнение получено подстановкой закона Фурье вместе с соотношением в уравнение баланса энергии . На практике закон Фурье применяется для описания тепловых процессов на макромасштабе. Однако закон Фурье предсказывает бесконечную скорость распространения сигнала, что может быть парадоксально с физической точки зрения. Изучение процессов на микроуровне, когда характерные длины пропорциональны нескольким длинам межатомных связей,выявило необходимость использования более сложных моделей теплопроводности, учитывающих конечную скорость распространения тепловых возмущений. Значительные отклонения от закона Фурье наблюдаются в одномерных кристаллических структурах . Недавние экспериментальные исследования одномерных наноструктур показали зависимость теплопроводности от длины структуры. Сильные отклонения от закона Фурье были экспериментально показаны для [math]\mathrm{C}[/math] и  [math]\mathrm{BN}[/math] нанотрубок. Тепловые аномалии, наблюдаемые в наноструктурах, могут быть использованы на практике для разработки перспективных устройств, таких как тепловой диод .

Аномальная природа тепловых процессов в одномерных кристаллических структурах была показана в работе , где рассматривалась задача о тепловом потоке между двумя тепловыми резервуарами. Множество результатов, посвященных аномальной природе распространения тепла в низкоразмерных структурах, собрано в книге . Модификация закона Фурье, приводящая к уравнению гиперболической теплопроводности (Максвелл, Каттанео, Веронотт, Лыков) , h + 1h = - T’ T + 1T = T” , где [math]\tau[/math] — время релаксации, одна из альтернатив классическому уравнению для описания подобных процессов. Однако, возникают сложности в применении его к описанию тепловых процессов в одномерных кристаллах, так как не удается однозначно определить время релаксации .

Перспективный подход к описанию нестационарных тепловых процессов в одномерных кристаллах предложен в . С использованием корреляционного анализа начальная стохастическая задача для отдельных частиц была сведена к детерминированной задаче для статистических характеристик кристалла. Ее решение дало континуальное уравнение , описывающее аномальное распространение тепла в одномерных гармонических решетках . Данная работа посвящена исследованию уравнения аномальной теплопроводности, сравнения его решений с решениями других уравнений, описывающих распространение тепла, сравнению различных подходов к определению производства энтропии в процессах распространения тепла.

Локализованные тепловые импульсы в одномерных кристаллических структурах

Уравнение аномальной теплопроводности в одномерном гармоническом кристалле

В данной главе будут получены точные аналитические решения этого уравнения, в частности, для начальных тепловых возмущений в форме прямоугольного, треугольного и пилообразного импульса. Такие свойства, как затухание и асимптотика теплового фронта будут исследованы подробно на примере прямо-угольного начального возмущения. Эти результаты могут быть использованы для анализа аномального распространения тепла в более сложных структурах, таких как одномерный гармонический кристалл на упругом основании , двумерный и трехмерный кристаллы . Понимание процессов аномального распространения тепла особенно важно для анализа экспериментальных данных, которые могут быть получены в ближайшем будущем в связи с активным развитием нанотехнологий.

Одномерный гармонический кристалл — это простая, но очень эффективная модель для изучения аномальных тепловых эффектов. Следуя работе , рассмотрим бесконечный гармонический кристалл. Каждая частица массой [math]m[/math] соединена с соседней частицей линейной пружиной жесткости [math]C[/math]. Уравнения движения частиц: [math]\ddot{u}_k = \omega_e^2( u_{k-1} - 2 u_k + u_{k+1}), \quad \omega_e = \sqrt{ \frac{C}{m}},[/math] где [math]u_k[/math] — отклонение от положения равновесия частицы с индексом [math]k[/math]. Рассматриваются следующие начальные условия: [math]\label{eq:particles_initial} u_k|_{t = 0} = 0, \qquad \dot{u}|_{t=0} = \sigma(x) \rho_k,[/math] где [math]\rho_k[/math] — независимые случайные величины с нулевым математическим ожиданием и единичной дисперсией; [math]\sigma[/math] — дисперсия начальных скоростей частиц, являющаяся медленно изменяющейся функцией пространственной координаты [math]x = ka[/math], где [math]a[/math]—начальное расстояние между соседними частицами. Данные начальные условия можно интерпретировать, как результат воздействия на кристалл ультракороткого лазерного импульса . Введем кинетическую температуру [math]T[/math]: [math]k_BT = m \langle \dot{u_k} \rangle^2,[/math] где [math]\langle ... \rangle[/math] оператор усреднения по реализациям, [math]k_B[/math] — постоянная Больцмана. В работе   было получено континуальное дифференциальное уравнение в частных производных: [math]\label{eq:temperature_equation} \ddot{T} + \frac{1}{t} \dot{T} = c^2 T'',[/math] где [math]c[/math] скорость звука в одномерном кристалле. Уравнение  описывает эволюцию пространственного теплового возмущения во времени. Следующие начальные условия для уравнения   соответствуют стохастической начальной задаче : [math]\label{eq:initial} \dot{T}|_{t=0} = 0, \qquad T|_{t=0} = T_0(x).[/math] Решение задачи – может быть получено в интегральной форме : [math] T(t,x) = \frac{1}{\pi} \int \limits_{-t}^t \frac{T_0(x - c\tau)}{\sqrt{ t^2 - \tau^2}} d\tau.[/math]

Уравнение частный случай уравнения Дарбу  . Данный тип уравнения был исследован в связи с решениями волнового уравнения в цилиндрической системе координат в двухмерном и трехмерном случаях. Однако оно не было изучено в связи с явлениями теплопроводности. Уравнение внешне схоже с уравнением гиперболической теплопроводности , однако имеет переменный коэффициент при слагаемом с первой производной по времени. Эта особенность возникает в связи с аномальной природой переноса тепла в одномерных структурах. Из структуры уравнения может показаться, что оно имеет сингулярность. Однако это не так, так как уравнение должно использоваться с начальными условиями , исключающими сингулярность. Отсутствие особенности подтверждается общим решением и частными решениями, которые будут рассмотрены далее.

Данная работа посвящена нахождению точных аналитических решений уравнения   для случаев, когда функция начального распределения [math]T_0(x)[/math] локализованная в пространстве функция координат [math]x[/math], [math]\label{eq:arbitrary_initial} T_0(x) = \begin{cases} 0, &x \lt -l, \\ \varPhi(x), &-l\lt x \lt l, \\ 0, &x \gt l, \end{cases}[/math] где [math]\varPhi(x)[/math] некоторая функция, [math]l[/math] — половина ширины локализованного возмущения. Экспериментально подобное начальное возмущение может быть получено путем сверхбыстрого нагрева лазером локализованного участка кристалла.

Прямоугольное возмущение

Решение

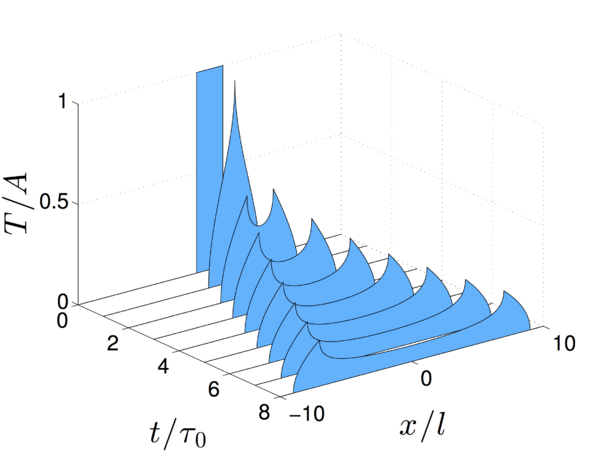
Рассмотрим прямоугольное начальное температурное распределение: [math]\label{eq:initial_step} T_0(x) = A\left( \mathcal{H}\left(x+l \right) - \mathcal{H}\left(x-l\right) \right),[/math] где [math]\mathcal{H}(x)[/math] — функция Хевисайда: [math]\mathcal{H}(x) = \begin{cases} 0, &x \lt 0, \\ 1, &x \ge 0. \end{cases}[/math] [math]A[/math] — амплитуда начального температурного возмущения. Подставляя формулу в решение получаем: [math]\label{eq:sum_heavy} T(t,x) = \frac{A}{\pi} \int \limits_{-t}^t \frac{ \mathcal{H}(x+l)}{\sqrt{ t^2 - \tau^2}}d\tau - \frac{A}{\pi} \int \limits_{-t}^t \frac{ \mathcal{H}(x-l)}{\sqrt{ t^2 - \tau^2}}d\tau.[/math] Воспользуемся решением для начального возмущения в виде функции Хевисайда : [math]\label{step_solution} T(x, t) \, = \, T_S(x, t) =\begin{cases} 0, & x \le - ct,\\ \cfrac{A}{\pi} \arccos\left(\cfrac{x}{ct}\right)& - ct \le x \le ct,\\ A, & x \ge ct. \end{cases}[/math] Подстановка формулы в интегральное представление дает искомое решение. Оно имеет вид: [math]\label{eq:step_solution0} t \le \tau_0: \qquad T(x, t) = \begin{cases} 0, & x \lt - l - ct;\\ A \left( 1 - \frac{1}{\pi} \arccos(\frac{x+l}{ct}) \right), & -l - ct \lt x \lt -l + ct;\\ A, &-l + ct \lt x \lt l -ct;\\ \frac{A}{\pi} \arccos(\frac{x-l}{ct}), &l - ct \lt x \lt l + ct;\\ 0, &x \gt l + ct, \end{cases}\hspace{3cm}[/math]

[math]\label{eq:step_solution} t \ge \tau_0: \qquad T(x, t) = \begin{cases} 0, &x \lt - l - ct;\\ A\left( 1 - \frac{1}{\pi} \arccos(\frac{x+l}{ct}) \right),& -l - ct \lt x \lt l - ct;\\ \frac{A}{\pi} \left( -\arccos(\frac{x+l}{ct}) + \arccos\frac{x-l}{ct} \right), &l - ct \lt x \lt -l + ct;\\ \frac{A}{\pi} \arccos(\frac{x-l}{ct}),& -l + ct \lt x \lt l + ct;\\ 0, &x \gt l + ct, \end{cases}[/math]

где [math]\tau_0 = l/c[/math]. Для отрицательных [math]x[/math] решение может быть получено из соображений симметрии как [math]T(x, t) = T(-x,t)[/math].

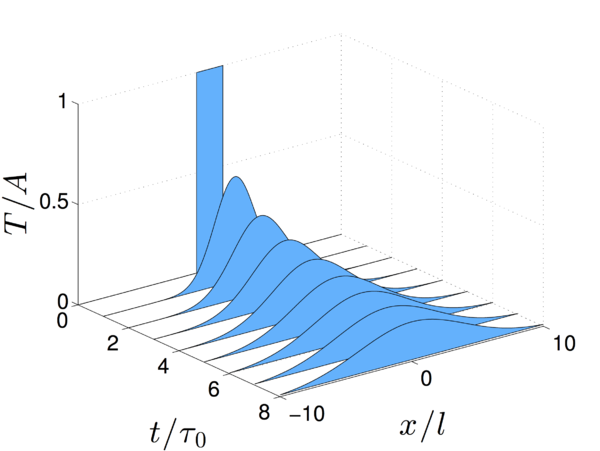
Для сравнения рассмотрим решение классического уравнения теплопроводности: [math]\label{eq:fourier} \dot{T} = \beta T''.[/math] Решение уравнения для начального распределения температуры в виде функции Хевисайда имеет вид  : [math]\label{eq:fourier_step_solution} T(x,t) = \frac{1}{2}\operatorname{erf}\left( \frac{x}{ \sqrt{ 4 \beta t}} \right),[/math] где [math]\operatorname{erf}(x)[/math] — функция ошибок Гаусса. Тогда решение : [math]T(x,t) = \frac{1}{2}\operatorname{erf}\left( \frac{x+l}{ \sqrt{ 4 \beta t}} \right) - \frac{1}{2} \operatorname{erf}\left( \frac{x-l}{ \sqrt{ 4 \beta t}} \right).[/math] Временная эволюция решений для уравнения аномальной теплопроводности   и классического уравнения теплопроводности  показана на Рис. . Сравним эти решения. У решения классического уравнения наблюдается максимум в точке [math]x=0[/math], который затухает экспоненциально. В случае аномальной теплопроводности решение затухает быстрее вблизи нуля [math]x=0[/math], формируя два максимума, которые распространяются в положительном и отрицательном направлениях и имеют координаты [math]x = -l + ct[/math] и [math]x = l - ct[/math].

Затухание

Рассмотрим затухание решения в точке [math]x = 0[/math] при больших временах. Представим решение в виде: [math]T(t, 0) = \frac{A}{\pi} \left[ \pi - 2\arccos\left( \frac{l}{ct} \right) \right] =2\varepsilon + O( \varepsilon^3),[/math] где [math]\varepsilon = \frac{l}{ct}[/math] малый параметр.

Теперь рассмотрим затухание максимумов с координатами [math] x = l -ct[/math] и [math] x = -l + ct[/math]. Из формулы  следует:

[math]\label{eq:max_fading_law} T(t, -l + ct) = T(t, l -ct)= \frac{A}{\pi}\left[ \pi - \arccos\left( \frac{2l}{ct} - 1\right) \right] = 2 \sqrt{ \varepsilon } + O\left( \varepsilon^\frac{3}{2} \right),[/math]

Обобщая вышесказанное, получаем: [math]T(t, 0) \stackrel { t \rightarrow \infty} {\sim} 2\varepsilon \sim \frac{1}{t}\;, \qquad T(t, -l + ct) = T(t, l - ct) \stackrel{t \rightarrow \infty}{ \sim } 2 \sqrt{\varepsilon} \sim \frac{1}{ \sqrt{t}}.[/math] Таким образом решение затухает быстрее в области начального возмущения (пропорционально [math]1/t[/math]) чем вблизи волнового фронта (пропорционально [math]1/ \sqrt{t}[/math]). Таким образом максимумы остаются ярко выраженными при больших временах.

Огибающая кривая

Решение имеет два максимума. Они распространяются в положительном и отрицательном направлениях со скоростью [math]c[/math]. Так как решение симметрично, будем рассматривать только максимум с координатами [math]x = ct-l[/math]. Найдем кривую, которую описывает точка максимума, по мере того, как волна движется в положительном направлении. Подставляя [math]t = \frac{x + l}{c}[/math] в формулу , получаем выражение для огибающей кривой: [math]T_{env}(x)= \frac{A}{\pi} \left[ \pi - \arccos \left( \frac{2l}{x+l} - 1\right) \right].[/math] для любых [math]x[/math] имеем: [math]T(x) \le T_{env} \left( |x| \right)[/math].

Огибающая кривая показана на Рис.[pic:envelope]. Выражение убывает как [math]1/\sqrt{x}[/math], что согласуется с тем, что решение вблизи волнового фронта затухает со временем как [math]1/ \sqrt{t}[/math] (волновой фронт движется с постоянной скоростью).

Асимптотическое поведение вблизи волнового фронта

Рассмотрим решение вблизи волнового фронта при больших временах [math]t[/math]. Положим [math]\xi = \frac{-x + ct}{l}[/math]. Для [math] x \in [-l+ct; l+ct] [/math] имеем: [math]\label{eq:rect_front_approx1} T(\xi, t) = \frac{A}{\pi} \arccos \left[ 1 - \frac{l}{ct}( \xi + 1) \right] \stackrel{ t \rightarrow \infty } {\sim} \frac{A}{\pi} \sqrt{ \frac{2l}{ct}} \sqrt{ \xi + 1},[/math] где [math]\cfrac{\xi + 1}{ct}[/math] — малый параметр, используемый для разложения. Для [math] x \in [l-ct; -l+ct][/math] имеем: [math]\label{eq:rect_front_approx2} \begin{aligned} T(\xi, t) = &\frac{A}{\pi} \left( - \arccos \left[ 1 - \frac{l}{ct} (\xi -1) \right] + \arccos \left[ 1- \frac{l}{ct}(\xi+1) \right] \right) \stackrel{ t \rightarrow \infty } {\sim} \\ \stackrel{ t \rightarrow \infty } {\sim} & \frac{A}{\pi} \sqrt{ \frac{2l}{ct}}\left( \sqrt{\xi+1} - \sqrt{\xi-1} \right). \end{aligned}[/math] Отметим, что функции и имеют вид: [math]\label{eq:step_assympt} T = \cfrac{A}{\pi}\sqrt{ \cfrac{2l}{ct} }\,F(\xi).[/math] График решения , выражения и соответствующие безразмерному временному параметру [math]t/\tau_0 = 100[/math] показан на Рис. [pic:step_wavefront_approx]. Выражение показывает, что решение сжимается вертикально со временем, но в остальном сохраняет свою форму. Асимптотические решения и достигают максимального значения температуры [math]T[/math] в точке [math]\xi=1[/math], при этом [math]F(\xi) = \sqrt{2}[/math]. Заметим,что решение в этой точке остается непрерывным, но имеет излом (производная по координате терпит разрыв).

Треугольное начальное возмущение

Для получения решения в случае треугольного начального возмущения рассмотрим вспомогательную задачу о линейно-нагретом полупространстве: [math]\label{eq:initial_linear} T_0(x) = \begin{cases} 0 , &x \lt 0 ;\\ Bx, &x \ge 0, \end{cases}[/math] где [math]B = A/l[/math] константа пропорциональности. Используется метод, описанный в . Т.к. распространения возмущения происходит со скоростью [math]c[/math], рассмотрим [math]x[/math] на промежутках: [math]\begin{aligned} &x \in [ -\infty; -ct ]: x -c \tau \lt 0, f = 0; \\ &x \in [ -ct; ct ]: x -c \tau \lt \gt 0, f = \begin{cases} 0, &\tau \lt \frac{x}{c}; \\ Bx, &\tau \gt \frac{x}{c}; \end{cases} \\ &x \in [ct; \infty] x - c\tau \gt 0, f = Bx. \end{aligned}[/math] Таким образом: [math]\begin{aligned} &x \in [ -\infty; -ct ]: T(t,x) =0; \\ &x \in [ -ct; ct ]: T(t,x) = \frac{B}{\pi} \int \limits_{-t}^{\frac{x}{c}} \frac{x - c\tau}{\sqrt{ t^2 - \tau^2}}d\tau = Bx\left( \frac{1}{\pi} \arcsin x + \frac{1}{2} \right) + \frac{B}{\pi} \sqrt{t^2 c^2 - x^2}; \\ &x \in [ ct; \infty ]: T(t,x) = Bx. \\ \end{aligned}[/math] Таким образом получаем решение для [math]|x| \lt ct[/math], [math]\label{eq:linear_solution} T(t,x) = \xi(t,x) = \begin{cases} 0, &x \lt -ct; \\ Bx\left( \frac{1}{\pi} \arcsin x + \frac{1}{2} \right) + \frac{A}{\pi} \sqrt{t^2 c^2 - x^2}, &x \lt |ct|;\\ Bx, &x \gt ct, \end{cases}[/math]

для [math]|x| \gt ct[/math] распределение температуры остается неизменным.

Теперь рассмотрим задачу о треугольном начальном тепловом возмущении: [math]\label{eq:triangle_initial} T_0(x) = \begin{cases} 0, &x\lt -l ,\\ (x+l)B, &-l \le x \lt 0,\\ (-x+l)B, &0 \le x \lt l,\\ 0, &x \ge l.\\ \end{cases}[/math] Очевидно, решение для начальных условий представляет собой линейную комбинацию: [math]\label{eq:triangle_solution} T(t,x) = T_L(t,x - l) + T_L(t, x+l) - 2T_L(t, x),[/math] где [math]T_L[/math] - решение для линейно-нагретого полупространства. Решение симметрично, [math]T(x,t) = T(-x,t)[/math]. Решение:

[math]\begin{aligned} t \le \tau_0/2 :\quad T(t,x) = \begin{cases} 0,& ~~~ x \lt -l - ct; \\ f(x+l), &~~~ -l - ct \lt x \lt -l + ct;\\ A(x+l) ,& ~~~ -l + ct \lt x \lt -ct;\\ f(x+l) - 2f(x),& ~~~ -ct \lt x \lt ct; \\ A(-x+l),&~~~ ct \lt x \lt l - ct;\\ A(-x+l) + f(x+l),& ~~~ l - ct \lt x \lt l + ct; \\ 0, &~~~ x \gt l + ct, \end{cases}\end{aligned}[/math]

[math]\begin{aligned} \tau_0/2 \le t \le \tau_0: \quad T(t,x) = \begin{cases} 0, &~~~ x \lt -l - ct; \\ f(x+l),& ~~~ -l - ct \lt x \lt -ct;\\ f(x+l) -2f(x) ,& ~~~ -ct \lt x \lt -l + ct;\\ A(x+l) - 2f(x), &~~~ -l+ct \lt x \lt l - ct; \\ A(x+l) + f(x-l) - 2f(x),&~~~ l-ct \lt x \lt ct;\\ A(-x+l) + f(x-l),& ~~~ ct \lt x \lt l + ct; \\ 0,& ~~~ x \gt l + ct, \end{cases}\end{aligned}[/math]

[math]\begin{aligned} t \ge \tau_0: \quad T(t,x) = \begin{cases} 0,& ~~~ x \lt -l - ct; \\ f(x+l),& ~~~ -l - ct \lt x \lt - ct;\\ f(x+l) -2f(x) ,& ~~~ -ct \lt x \lt l - ct;\\ f(x+l) + f(x-l) - 2f(x), &~~~ l -ct \lt x \lt -l + ct; \\ A(x+l) + f(x-l) - 2f(x),&~~~ - l + ct \lt x \lt ct;\\ A(-x+l) + f(x-l), &~~~ ct \lt x \lt l + ct; \\ 0, &~~~ x \gt l + ct. \end{cases}\end{aligned}[/math]

График решения для треугольного начального возмущения показан на Рис. [pic:triangle_solution].

В отличие от прямоугольного теплового возмущения, для треугольного возмущения решение всюду гладкое: и в начале волнового фронта, и в точке максимума.

Пилообразное возмущение

Рассмотрим начальное возмущение, заданное в виде пилообразного импульса: [math]\label{eq:sawtooth_initial} \begin{aligned} T_0(x) = \begin{cases} 0, &\quad x \le -l ,\\ x+l, &\quad -l \le x \lt 0,\\ 0, &\quad 0 \le x.\\ \end{cases} \end{aligned}[/math] Начальное возмущение может быть записано как линейная комбинация линейно нагретого полупространства и функции Хевисайда. Тогда решение для пилообразного возмущения может быть получено как линейная комбинация решений для функции Хевисайда [math]T_S(x,t)[/math] и линейно-нагретого полупространства [math]T_L(x,t)[/math]: [math]T(t,x) = T_L(x+l,t) + T_L(x,t)+T_S(x,t),[/math] оно имеет следующий кусочно-заданный вид: [math]t \le \tau_0: \quad T(x, t)= \begin{cases} 0, & x \le - l - ct,\\ f (x+l), & -l - ct \le x \le -l + ct,\\ B x, &-l + ct \le x \le -ct,\\ Bx - f(x) - \frac{A}{\pi} \arccos(\frac{x}{ct}), & -ct \le x \le ct,\\ 0, &x \gt ct, \end{cases}[/math]

[math]\label{eq:saw_solution} t \ge \tau_0: \quad T(x, t) = \begin{cases} 0, &x \le -ct - l ,\\ f (x+l)& - ct -l \le x \le -ct,\\ f (x+l) - f(x) - \frac{A}{\pi} \arccos(\frac{x}{ct}), & - ct \le x \le ct - l ,\\ B x - f(x) - \frac{A}{\pi} \arccos(\frac{x}{ct}),& ct -l \le x \le ct,\\ 0, & ct \le x. \end{cases}[/math]

График решения представлен на Рис. [pic:sawtooth_solution]. Тепловая волна, распространяющаяся в отрицательном направлении, имеет гладкое начало и излом с бесконечной производной в точке максимума. Напротив, тепловая волна, распространяющаяся в положительном направлении, имеет вертикальную касательную в начале и гладкое поведение в точке максимума.

Затухание произвольного локализованного импульса

Рассмотрим произвольный ограниченный симметричный импульс следующего вида: [math]T_0 = \begin{cases} 0, &x \lt -a; \\ \Phi(x), &-a \lt x \lt a; \\ 0, &x \gt a. \end{cases}[/math] Рассматриваются большие значения [math]t[/math]. [math]\Phi(x)[/math] — ограничена, четная. [math] x \lt \lt ct[/math]. Тогда [math]T_0( x - c \tau) \sim T_0( - c \tau)[/math], [math]a \lt \lt ct[/math]. Тогда уравнение ([eq:temperature]) запишется в следующем виде: [math]\label{eq:temperature_fade} T(t,x) = \frac{1}{\pi} \int \limits_{-t}^t \frac{T_0(x - c\tau)}{\sqrt{ t^2 - \tau^2}}d\tau \sim \frac{1}{\pi} \int \limits_{-t}^t \frac{T_0( - c\tau)}{\sqrt{ t^2 - \tau^2}}d\tau.[/math]

Затухание вблизи нуля

При [math]t \gt \gt 1[/math] и [math] \tau \lt \lt 1[/math]: [math]\frac{1}{ \sqrt{ t^2 - \tau^2}} \sim \frac{1}{t}[/math] Тогда уравнение ([eq:temperature_fade]) запишется: [math]\frac{1}{\pi} \int \limits_{-t}^t \frac{T_0( - c\tau)}{\sqrt{ t^2 - \tau^2}}d\tau \sim \frac{1}{\pi t} \int \limits_{-\frac{a}{c}}^ \frac{a}{c} T_0(-c \tau) d \tau,[/math] [math]\int \limits_{0}^t T_0(-c \tau) d \tau = \int \limits_{0}^ \frac{a}{c} T_0(-c \tau) d \tau + \int \limits_{ \frac{a}{c}}^t T_0(-c \tau) d \tau = \int \limits_{0}^ \frac{a}{c} T_0(-c \tau) d \tau[/math] Таким образом [math]\int \limits_0^t T_0(-c \tau) d \tau[/math] не зависит от [math]t[/math]. Тогда: [math]\int \limits_0^t T_0(-c \tau) d \tau = C_1[/math]. Можно говорить о том, что на больших временах функция температуры затухает вблизи нуля как [math] \frac{1}{t}[/math]: [math]T(t,x) \stackrel{ t \rightarrow \infty } {\sim} \frac{1}{t}[/math]

Затухание вблизи фронта волны

Рассмотрим [math]x \sim ct[/math]. Представим [math]x[/math] в виде [math]x = c\xi[/math]. [math]\label{eq:temperature_front} \begin{aligned} T(t,x) &= \frac{1}{\pi} \int \limits_{-t}^t \frac{T_0(x - c\tau)}{\sqrt{ t^2 - \tau^2}}d\tau = \frac{1}{\pi} \int \limits_{-t}^t \frac{T_0( c (\xi - \tau) )}{\sqrt{ t^2 - \tau^2}}d\tau = \\&= \frac{1}{\pi} \int \limits_{-t}^{\xi - \frac{a}{c}} \frac{T_0( c (\xi - \tau) )}{\sqrt{ t^2 - \tau^2}}d\tau + \frac{1}{\pi} \int \limits_{\xi - \frac{a}{c}}^{\xi + \frac{a}{c}} \frac{T_0( c (\xi - \tau) )}{\sqrt{ t^2 - \tau^2}}d\tau +\frac{1}{\pi} \int \limits_{\xi + \frac{a}{c}}^t \frac{T_0( c (\xi - \tau) )}{\sqrt{ t^2 - \tau^2}}d\tau = \\&= \frac{1}{\pi} \int \limits_{\xi - \frac{a}{c}}^{\xi + \frac{a}{c}} \frac{T_0( c (\xi - \tau) )}{\sqrt{ t^2 - \tau^2}}d\tau. \end{aligned}[/math] Т.к. [math]x \sim ct[/math], то [math]\xi \sim t[/math]. При интегрировании [math]\tau[/math] изменяется от [math]\xi - \frac{a}{c} \sim t - \frac{a}{c} [/math] до [math]\xi + \frac{a}{c} \sim t + \frac{a}{c} [/math]. Можно разложить подынтегральную функцию [math] \frac{1}{ \sqrt{t^2 - \tau^2} }[/math] по [math]\tau[/math] в окрестности точки [math]t[/math]. [math]\frac{1}{ \sqrt{t^2 - \tau^2} }= \frac{1}{\sqrt{2t} \sqrt{t-\tau}} + O\left( \left(\frac{1}{t - \tau} \right)^{\frac{3}{2}} \right).[/math] Уравнение ([eq:temperature_front]) записывается в виде: [math]\frac{1}{\sqrt{2} \pi} \frac{1}{ \sqrt{t}} \int \limits_{\xi - \frac{a}{c}}^{\xi + \frac{a}{c}} \frac{T_0( c (\xi - \tau) )}{\sqrt{ t - \tau}}d\tau.[/math] Проведем замену переменной в интеграле: [math]\zeta = \xi - \tau[/math]. [math]T(t,x) = \frac{1}{\sqrt{2} \pi} \frac{1}{ \sqrt{t}} \int \limits_{ -\frac{a}{c}}^{\frac{a}{c}} \frac{T_0( c \zeta )}{\sqrt{ t - \xi + \zeta }}d\zeta \stackrel{ \xi \sim t} {\longrightarrow} \frac{1}{\sqrt{2} \pi} \frac{1}{ \sqrt{t}} \int \limits_{ -\frac{a}{c}}^{\frac{a}{c}} \frac{T_0( c \zeta )}{\sqrt{ \zeta }}d\zeta.[/math] Можно говорить о том, что на больших временах вблизи фронта волны функция температуры затухает как [math] \frac{1}{\sqrt{t}}[/math]: [math]T(t,x) \stackrel{ t \rightarrow \infty } {\sim} \frac{1}{ \sqrt{t}}[/math]

Ассимптотическое представление решения при больших временах на всем интервале [math]x[/math]

Рассмотрим решение ([eq:temperature]) на масштабах [math]x \sim ct[/math] и больших значениях [math]t[/math]. Т.к. функция [math]T_0(x) = 0[/math] на интервалах [math]x \in [-\infty; -a][/math] и [math]x \in [a; \infty][/math], заменой [math]\xi = x - c \tau[/math] получается:

[math]\begin{aligned} T(t,x) &= \frac{A}{\pi} \int \limits_{-t}^t \frac{T_0(x - c\tau)}{\sqrt{ t^2 - \tau^2}}d\tau = \frac{A}{\pi} \int \limits_{-a}^a \frac{T_0( \xi )}{\sqrt{c^2 t^2 - (\xi + x)^2}}d\xi \label{eq:temp_asympt}.\end{aligned}[/math]

Формула [eq:temp_asympt] при [math]t \rightarrow \infty[/math] приобретает вид [math]T(t,x) = \frac{A}{\pi} \frac{1}{ \sqrt{c^2 t^2 - x^2}} \int \limits_{-a}^a T_0( \xi )d\xi.[/math] Подобный вид имеет решение уравнения ([eq:temperature]) для начального условия в виде [math]\delta(x)[/math].

Обсуждения

В работе рассмотрен процесс распространения тепла в одномерном гармоническом кристалле. Исследована эволюция локализованных тепловых возмущений. Построены решения для уравнения, описывающего аномальное распространение тепла , выведенного в работе . Получены точные аналитические решения для прямоугольного, треугольного и пилообразного начального возмущения. Показано, что в отличие от классического уравнения теплопроводности, решения уравнения имеют четко выраженный волновой фронт. Для прямоугольного теплового возмущения показано, что затухание решения вблизи волнового фронта пропорционально [math]1/\sqrt{t}[/math] , а вблизи нуля пропорционально [math]1/t[/math]. Таким образом решение затухает медленнее вблизи волнового фронта, в результате чего наблюдаются четко выраженные максимумы. Решение вблизи волнового фронта описывается функцией, обратно пропорциональной корню из времени, и имеет вид: [math]T = \cfrac{A}{\pi}\,\sqrt{ \cfrac{2l}{ct} }\,F(\xi) [/math].

Решение для треугольного начального возмущения имеет гладкое начало и гладкое поведение в точке максимума.

В случае пилообразного начального возмущения реализуется несимметричное решение: левый волновой фронт имеет гладкое начало и бесконечную производную в точке максимума; правый имеет бесконечную производную в начале, гладкое поведение и горизонтальную касательную в точке максимума. Полученные решения демонстрируют волновую природу и степенное затухание. Это отличает полученные решения от решений классического уравнения теплопроводности  (диффузионный характер, экспоненциальное затухание) и гиперболического уравнения теплопроводности   (волновой характер, экспоненциальное затухание). Свойства полученных решений могут быть использованы для анализа экспериментальных данных и выбора подходящей модели описания процесса. Работа выполнена при поддержке Российского научного фонда [грант 14-11-00599].

Более сложные системы

Одномерный кристалл с внутренней массой

Рассмотрим бесконечную гармоническую цепочку , каждая частица массой [math]M[/math] которого содержит внутреннюю степень свободы в виде массы [math]m[/math] на упругом основании. Уравнения движения записываются следующим образом: [math]\begin{aligned} \label{eq:motion} &M\ddot{u}_i = C( u_{i-1} - 2u_i + u_{i+1}) - C_1(u_p - v_p),\\ &m\ddot{v}_i = C_1(u_i - v_i), \end{aligned}[/math] где [math]u[/math] — перемещения частиц массой [math]M[/math], [math]v[/math] — перемещения частиц массой [math]m[/math]. Далее будем рассматривать векторные величины [math]\textbf{s}_i = \left[ \begin{array} {cc}u_i & v_i \end{array} \right]^T[/math]. Тогда уравнение ([eq:motion]) может быть записано в операторном виде: [math]\ddot {\mathbf{s}}_i = \mathcal{L} \cdot \mathbf{s}_i,[/math] где [math]\mathcal{L} = \left[ \begin{array}{cc} \omega_1^2 \Delta^2 & \omega_2 \\ \omega_3^2 & - \omega_3 \end{array} \right],[/math] где [math]\Delta f_i = f_{i-1} - 2f_i + f_{i+1}[/math], [math]\omega_1 = \sqrt{ \frac{C}{M} }[/math], [math]\omega_2 = \sqrt{ \frac{C_1}{M} }[/math], [math]\omega_3 = \sqrt{ \frac{C_1}{m} }[/math]. начальный момент времени перемещения и скорости частиц задаются следующим образом: [math]t=0: \quad \mathbf{s}_i^0 = \left[ \begin{array}{c} u_i^0 \\ v_i^0 \end{array} \right], \quad \mathbf{\dot{s}}_i^0 = \left[ \begin{array}{c} \dot{u}_i^0 \\ \dot{v}_i^0 \end{array} \right],[/math] Где [math] \textbf{s}_i, \textbf{s}_i[/math] - независимые случайные векторы с нулевым матожиданием. Уравнения ([eq:motion]) полностью описывают динамику кристалла, они могут быть решены численно или аналитический, однако для описания макроскопических характеристик больший интерес представляет изменение статистических характеристик.

Рассмотрим ковариации перемещений и скоростей двух частиц с индексами [math]p[/math] и [math]q[/math]. Частицы, соответствующие внутренним степеням свободы будут иметь те же индексы. Для описания статистических характеристик такой системы потребуется рассматривать матрицы ковариаций соответствующих величин: [math]\label{eq:covariations} \begin{gathered} \xi_{pq} = \left\lt \mathbf{s}_p \mathbf{s}_q \right\gt = \left[ \begin{array}{cc} \left\lt u_p u_q\right\gt & \left\lt u_p v_q\right\gt \\ \left\lt v_p u_q\right\gt & \left\lt v_p v_q\right\gt \end{array} \right], \quad \kappa_{pq} = \left\lt \mathbf{\dot{s}}_p \mathbf{\dot{s}}_q \right\gt = \left[ \begin{array}{cc} \left\lt \dot{u}_p \dot{u}_q\right\gt & \left\lt \dot{u}_p \dot{v}_q\right\gt \\ \left\lt \dot{v}_p \dot{u}_q\right\gt & \left\lt \dot{v}_p \dot{v}_q\right\gt \end{array} \right], \\ \nu_{pq} = \left\lt \mathbf{s}_p \mathbf{\dot{s}}_q \right\gt = \left[ \begin{array}{cc} \left\lt u_p \dot{u}_q\right\gt & \left\lt u_p \dot{v}_q\right\gt \\ \left\lt v_p \dot{u}_q\right\gt & \left\lt v_p \dot{v}_q\right\gt \end{array} \right]. \end{gathered}[/math] Стоит отметить, что [math]\xi_{pq} = \xi_{qp}^T[/math], [math]\kappa_{pq} = \kappa_{qp}^T[/math].

Дифференцируя систему ([eq:covariations]), получаем следующие соотношения: [math]\label{eq:1st_order} \begin{gathered} \dot{\xi}_{pq} = \nu_{pq}+\nu_{qp}^T, \quad \dot{ \kappa} = \mathcal{L} \cdot \nu_{pq} + \left( \mathcal{L} \cdot \nu_{pq} \right)^T, \quad \dot{ \nu}_{pq} = \kappa + \xi_{pq} \cdot \mathcal{L}^T. \end{gathered}[/math] Повторное дифференцирование позволяет исключить смешаные ковариации и получить систему 2-го порядка относительно ковариаций перемешений и скоростей:

[math]\label{eq:2nd_order} \begin{gathered} \ddot{\xi}_{pq} = 2 \kappa_{pq} + \mathcal{L} \cdot \xi_{pq} + \xi_{pq} \cdot \mathcal{L}^T, \quad \ddot{ \kappa}_{pq} = 2 \mathcal{L} \cdot \xi_{pq} \cdot \mathcal{L}^T + \mathcal{L} \cdot \kappa_{pq} + \kappa_{pq} \cdot \mathcal{L} ^ T. \end{gathered}[/math]

Выразив из первого уравнения ([eq:2nd_order]) [math]\kappa_{pq}[/math] и подставив во второе, получаем уравнение 4-го порядка для матрицы ковариаций перемещений: [math]\label{eq:4th_order} \ddddot{\xi_{pq}} - 2\left( \mathcal{L} \cdot \ddot{ \xi }_{pq} + \ddot{ \xi }_{pq} \cdot \mathcal{L}^T \right) + \mathcal{L}^2 \cdot \xi_{pq} - 2 \mathcal{L} \cdot \xi_{pq} \cdot \mathcal{L}^T + \xi_{pq} \cdot {\mathcal{L}^T}^2 = 0.[/math] Стоит отметить, что уравнению ([eq:4th_order]) также удовлетворяет [math] \kappa_{pq}[/math].

Начальные условия к уравнениям ([eq:1st_order]), ([eq:2nd_order]), ([eq:4th_order]) определяются начальными скоростями и перемещениями частиц. [math]\xi_{pq} = \left\lt \mathbf{s}_p^0 \mathbf{s}_q^0 \right\gt , \quad \kappa_{pq} = \left\lt \mathbf{\dot{s}}_p^0 \mathbf{\dot{s}}_q^0 \right\gt , \quad \nu_{pq} = \left\lt \mathbf{s}_p^0 \mathbf{\dot{s}}_q^0 \right\gt [/math] Таким образом, для ковариаций, получаем замкнутую систему уравнений с детерминированными начальными условиями.

Обсуждения

В данной главе выработан подход к описанию стохастических процессов для системы с двумя степенями свободы. Показано, что необходимо рассматривать не скалярные, а матричные величины. Получено детерминированное уравнение для усредненных стохастических величин. На основании этого уравнения в дальнейшем могут быть получены уравнения, описывающие распространение тепла в подобных системах. Существенным вопросом дальнейших исследований является определение температуры. Для двухмерной решетки было показано, что температура является тензорной величиной и энергии распределяются независимо по степеням свободы. Также для диатомного кристалла было показано, что частицы с разными массами в стационарном процессе могут иметь разные температуры. Дальнейшее исследование уравнения и нахождение его интегралов поможет найти определение температуры для подобных систем.

Заключение

В работе рассматриваются особенности нестационарных процессов в одномерных гармонических кристаллах. Рассматривается аномальное уравнение теплопроводности, полученное в работе .

В Главе 1 получены и исследуются свойства решений для локализованных тепловых возмущений. Проводится сравнение полученных результатов с классическим уравнением теплопроводности. На примере полученных решений видно, что баллистическое распространение тепла имеет волновой характер, распространение тепловых волн происходит с конечной скоростью.

В Главе 2 проведено сравнение с решением точной дискретной задачи. Показано, что краевые эффекты, вызванные мгновенной скоростью возмущения, наблюдаются только на масштабах, сопоставимых с равновесным межатомным расстоянием. На масштабах, на которых гармонический кристалл может быть рассмотрен как сплошная среда, эти эффекты имеют незначительный характер и при рассмотрении определенных задач ими можно пренебречь.

Подобные процессы имеют как волновой, так и диффузионный характер. При этом уравнение баллистического распространения тепла является обратимым по времени (замена [math]t[/math] на [math]-t[/math] не изменяет уравнение). Полученные в Главе 3 результаты показали, что вообще говоря это не означает физическую необратимость. Для того, чтобы выяснить характер диффузии и меру необратимости было рассмотрено производство энтропии рассматриваемых процессов. Было показано, что классическая формулировка второго закона термодинамики приводит к противоречию в случае гиперболического и баллистического уравнений теплопроводности. Было показано, что для этих уравнений требуются дополнительные переменные состояния, которые учитывают тепловые потоки и время.

Приведенные результаты описывают свойства нестационарных тепловых процессов в одномерном гармоническом кристалле. Однако интересны для рассмотрения и более сложные модели такие как: двумерный кристалл, одномерный кристалл с частицами разной массы. Рассмотрение данных моделей имеет не только фундаментальный характер а может применяться для описания двухатомных кристаллов, или распределения энергий по внутренним степеням свободы (например по электронным степеням свободы). В Главе 4 был рассмотрен гармонический кристалл с внутренней массой. Получено детерминированное уравнение для ковариаций перемещений. В подобных системах температура может определяться отдельно для каждой степени свободы. Получение уравнений для распространения температур является темой для дальнейших исследований.

Автор благодарен Е.Н. Вильчевской, Е.А. Ивановой, В.А. Кузькину, В. Мюллеру, А.Б. Фрейдину за полезные обсуждения.