Разработка электро-механических моделей углеродных нановискеров как детекторов масс

МАГИСТЕРСКАЯ РАБОТА
Автор работы: Ванюшкина Валентина
Научный руководитель: Л.В. Штукин

Введение

Наноструктуры - объекты, созданные человеком и имеющие малые размеры (от нескольких нанометров до сотен микрометров). Эта область науки открывает много новых и интересных возможностей для экспериментов и теоретических расчётов. Наноструктуры могут быть очень полезны для медицины, механики, инженерии и биологии: могут быть ис- пользованы для разрезания клеток, взвешивания объектов на нано- и микро- уровнях, а так же для построения более сложных структур. Одной из технологий для создания наноструктур является напыление аморфного углерода на металлическую иглу. Целью данной работы является подробное исследование двух углеродных наноструктур Одна из них это прямолинейный одиночный вискер. Длина такого вискера порядка несколь- ких микрометров, а максимальная толщина всего лишь несколько десятков нанометров. Вис- кер выращен на вершине металлической иглы и закреплен на ней. Вторая исследуемая кон- струкция, это система из двух вискеров, связанных между собой упругой перемычкой. Пере- мычка так же создана из углерода путём напыления. Задачи данной работы заключаются в исследовании и описании одного из экспериментов с одиночным вискером на игле с помощью применения приближённого метода решения; опи- сание модели и изучение дифференциального резонатора из нановискеров для возможного применения его в качестве детектора масс; изучения одного из способов точного измерения колебаний нановискера и дифференциального резонатора с помощью различных емкостных датчиков.

Двойной вискер

Одиночный вискер

Задача о вискере, колеблющемся на игле

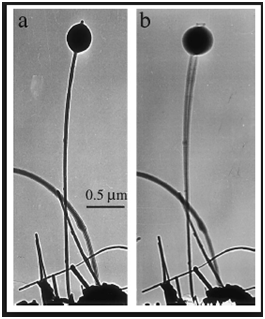
Первая исследуемая конструкция представляет из себя одиночный прямой вискер, колеб- лющийся на игле. В ходе одного из экспериментов над такой системой было обнаружено, что существует две близкие собственные частоты этой системы с похожими формами колебаний.

Колебания одиночного вискера на игле

Для построения приближённого решения задачи о двух балках используется метод, предложенный В.М.Фридманом, заключающемся в использовании спектральных свойств отдельных элементов системы. В соответствии с работой уравнения движения системы балок могут быть для удобства записаны в операторном виде. [math]\xi=\left( \begin{array}{cc} Q\\ M \end{array} \right) \qquad \eta=\left( \begin{array}{cc} w\\ \theta \end{array} \right)[/math] [math]D=\left( \begin{array}{cc} -\frac{\partial }{\partial x} & 0\\ 1 & -\frac{\partial }{\partial x} \end{array} \right) \qquad D^*=\left( \begin{array}{cc} \frac{\partial }{\partial x} & 1\\ 0 & \frac{\partial }{\partial x} \end{array} \right)[/math] [math]R=\left( \begin{array}{cc} \rho & 0\\ 0 & j \end{array} \right) \qquad B=\left( \begin{array}{cc} b & 0\\ 0 & \beta \end{array} \right)[/math] [math]\int\limits_0^l D \xi \eta \,dx +\xi\eta\bigg|_{x=0}^{x=l} = \int\limits_0^l \xi D^* \eta \,dx[/math]

Модель нановесов

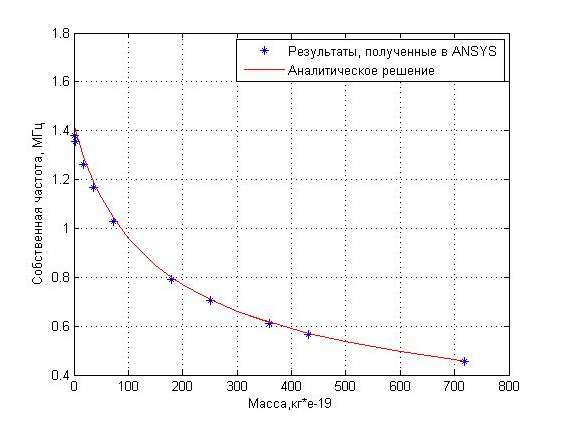
Исследуемые весы сделаны из углеродных наноструктур, называемых одиночными вискерами. Это углеродная балка очень маленьких размеров. На нее падает частица с некоторой скоростью, в результате чего вискер начинает колебаться. Исследовав колебания вискера, можно будет определить массу объекта, упавшего на вискер. Для этого была построена конечноэлементная модель вискера с точечной массой на правом конце и заделкой на левом. Проведен расчет собственных частот и форм колебаний, а так же найдено аналитическое решение:[math]f = \sqrt\frac{3E(\frac{d}{2})^4}{16\pi (0.227*m_1+M)l^3}[/math], где [math]f [/math] -собственная частота колебаний системы.

Нановесы

Было проведено сравнение результатов, полученных аналитически и методом конечных элементов.

Сравнение зависимости собственной частоты от массы взвешиваемого объекта в зависимости от метода решения.

Конечноэлементное моделирование сложных структур.

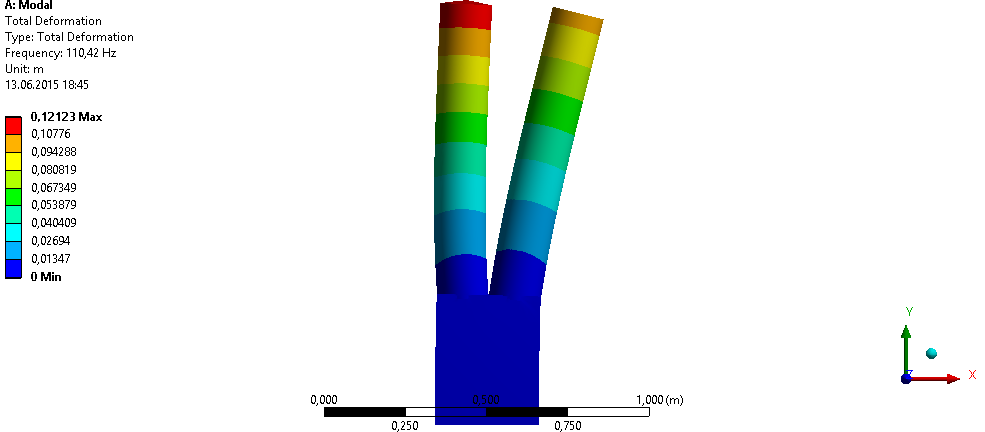
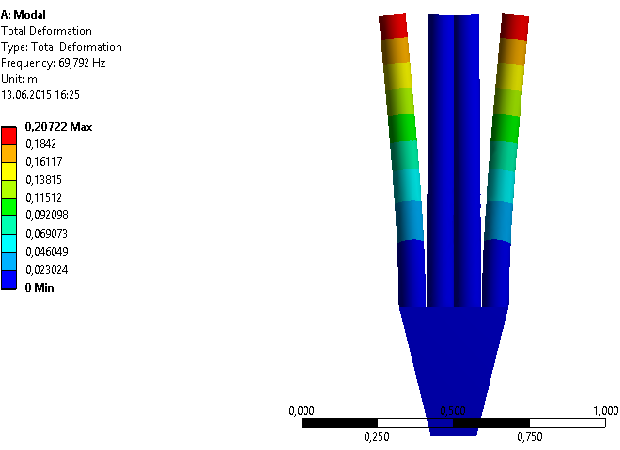
Для рассмотрения колебаний сложных структур, были созданы их конечноэлементные мо- дели и проведен расчет собственных и вынужденных колебаний.При создании моделей, бы- ли использованы размеры реальных наноконструкций, но увеличенные в 106 раз, так как в программном пакете ANSYS Workbench не предусмотрена работа с наноразмерами, однако понятно, что собственные формы не изменятся, а значения частот уменьшатся в 106 раз, не меняя при этом свое мантиссы. Некоторые из получившихся результатов представлены ниже.

Выводы

В данной работе проведено исследование продольных и поперечных колебаний вискера на игле с помощью представления этой системы в виде механической системы с двумя степенями свободы. Для продольных и поперечных колебаний были найдены аналитически уравнения движения и созданы интерактивные модели.Эти модели позволяют анализировать текущее движение системы в зависимости от параметров вискера и иглы. В дальнейшем к данной части работы будет добавлена модель с постоянным гармоническим воздействием на иглу, что позволит исследовать колебания, более приближенные к реальным и рассмотреть случай динамического гашения колебаний вискера. Так же была рассмотрена модель нановесов для случая падения массы точно на конец вискера. Были смоделированы сложные конструкции из вискеров, такие как вилка, скальпель и камертон. При моделировании этих конструкции мы получили два набора собственных частот (два спектра), так как модели трехмерные. Полезны собственные частоты и формы только в плоскости самой конструкции, так как при реальных экспериментах колебания происходят именно в этих плоскостях. Найдены только первые две собственные частоты каждого спектра, это объясняется тем, что чем ниже порядок частоты, тем проще попасть в нее при реальных экспериментах. Практически невозможно попасть в резонанс с третей и выше собственными частотами. Для модели вискера на игле представлены только две собственные формы, так как эта модель осесимметрична и ее спектры и собственные формы, соответствующие частотам этих двух спектров совпадают,но располагаются в разных плоскостях. В дальнейшем, планируется решить полностью задачу нановесов, составив систему уравнений, для нахождения собственных частот; исследовать более сложные конструкции, например трехмерные; создать интерактивную модель динамического гасителя колебаний. Продолжение данного исследования необходимо, так как направление экспериментального создания вискеров развивается очень быстро. За последний год были построены и исследова- ны гораздо более сложные конструкции и найдены новые пути их применения. Но каждый эксперимент трудоемок, сложен и требует как финансовых, так и ресурсных затрат. В будущем планируется предсказывать результаты эксперементов с целью сокращения их числа и достижения максимальной эффективности работы специалистов-экспериментаторов.

Список литературы

• Z.L.Wang, P.Poncharal, W.A. de Heer. Measuring physical and mechanical properties of individual carbon nanotubes by in situ TEM. J. Phys. Chem. Solids, 2000, 61(7), pp.1025- 1030
• Dynamik der Baukonstruktionen, Christian Petersen 2000 1st edition,722 [3] И.М.Бабаков. Теория колебаний.1968,3
• Я.С.Гринберг, Ю.А.Пашкин, Е.В.Ильичев. Наномеханические резонаторы.2012.
• Mai Duc Dai, Chang-Wan Kim, Kilho Eom. Nonlinear vibration of graphene resonators and their applications in sensitive mass detection. Nanoscale Research Letters 2012 7:499
• Новопашенный Г.Н. Электронные измерительные приборы. 1966. 268