Мещерский задача 4.43
Материал из Department of Theoretical and Applied Mechanics
Мещерский Задача 7.10
Визуализация 3D-задачи по статике на JavaScript
Исполнитель: ["Уманский Александр"]
Группа 23604/1 Кафедра Теоретической механики
Формулировка задачи
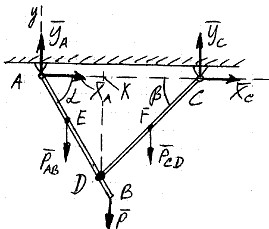
Подвеска состоит из двух балок AB и CD, соединенных шарнирно в точке D и прикрепленных к потолку шарнирами A и C. Вес балки AB равен 60 Н и приложен в точке E. Вес балки CD равен 50 Н и приложен в точке F. В точке B к балке AB приложена вертикальная сила P=200 Н. Определить реакции в шарнирах A и C, если заданы следующие размеры: AB=1 м; CD=0,8 м; AE=0,4 м; CF=0,4 м; углы наклона балок AB и CD к горизонту соответственно равны: α=60° и β=45°.
Решение задачи
<syntaxhighlight lang="javascript" line start="1" enclose="div">
<!DOCTYPE html>
<head>
<meta charset = "utf-8"> <script src = "http://tm.spbstu.ru:8090/ws-htmlets/Umanskij_AO/4.43%20%D0%9C%D0%B5%D1%89%D0%B5%D1%80%D1%81%D0%BA%D0%B8%D0%B9/Three.js"></script> <script src = "http://tm.spbstu.ru:8090/ws-htmlets/Umanskij_AO/4.43%20%D0%9C%D0%B5%D1%89%D0%B5%D1%80%D1%81%D0%BA%D0%B8%D0%B9/stats.min.js"></script> <script src = "http://tm.spbstu.ru:8090/ws-htmlets/Umanskij_AO/4.43%20%D0%9C%D0%B5%D1%89%D0%B5%D1%80%D1%81%D0%BA%D0%B8%D0%B9/OrbitControls.js"></script> <script src = "http://tm.spbstu.ru:8090/ws-htmlets/Umanskij_AO/4.43%20%D0%9C%D0%B5%D1%89%D0%B5%D1%80%D1%81%D0%BA%D0%B8%D0%B9/dat.gui.js"></script> <style> body { margin:0; overflow:hidden; } </style>
</head> <body>
<script>
var renderer, scene, camera, stats, stairs1,stairs2;
var RA, RAx, RAy, RB, RBx, RBy, P, Pab, Pcd;
var step = 0;
var controls = new function()
{
this.alpha1 = Math.PI / 3;
this.alpha2 = Math.PI / 6;
this.length1 = 4;
this.length2 = 10;
this.gamma = 1/2;
this.Pab = 1;
this.Pcd = 1;
this.P = 1;
this.PositionPab = 1/2;
this.PositionPcd = 1/2;
}
var gui = new dat.GUI();
gui.add(controls, 'alpha1', 0, Math.PI / 2).onChange(Refresh_Scene);
gui.add(controls, 'alpha2', 0.1, Math.PI / 3).onChange(Refresh_Scene);
gui.add(controls, 'length1', 1, 10).onChange(Refresh_Scene);
gui.add(controls, 'gamma', 0, 1).onChange(Refresh_Scene);
gui.add(controls, 'P', 0, 10).onChange(Refresh_Scene);
gui.add(controls, 'Pab', 0, 10).onChange(Refresh_Scene);
gui.add(controls, 'Pcd', 0, 10).onChange(Refresh_Scene);
gui.add(controls, 'PositionPab', 0, 1).onChange(Refresh_Scene);
gui.add(controls, 'PositionPcd', 0, 1).onChange(Refresh_Scene);
function Stairs_Pos()
{
scene.remove(stairs1);
scene.remove(stairs2);
var stairsM = new THREE.LineBasicMaterial({color: 0x000000});
var stairs1G = new THREE.Geometry();
stairs1G.vertices.push(new THREE.Vector3(0, 0, 0));
stairs1G.vertices.push(new THREE.Vector3(controls.length1 * Math.cos(controls.alpha1), -controls.length1 * Math.sin(controls.alpha1), 0));
stairs1 = new THREE.Line(stairs1G, stairsM);
scene.add(stairs1);
var stairs2G = new THREE.Geometry();
stairs2G.vertices.push(new THREE.Vector3(controls.gamma * controls.length1 * Math.cos(controls.alpha1),controls.gamma*(-controls.length1 * Math.sin(controls.alpha1)) , 0));
stairs2G.vertices.push(new THREE.Vector3(controls.gamma * controls.length1 * Math.sin(controls.alpha1) * Math.cos(controls.alpha2)/Math.sin(controls.alpha2), 0, 0));
stairs2 = new THREE.Line(stairs2G, stairsM);
scene.add(stairs2);
}
function Forces_Remove()
{
scene.remove(RA);
scene.remove(RAx);
scene.remove(RAy);
scene.remove(RB);
scene.remove(RBx);
scene.remove(RBy);
scene.remove(P);
scene.remove(Pab);
scene.remove(Pcd);
}
function Forces_Push()
{
scene.add(RA);
scene.add(RAx);
scene.add(RAy);
scene.add(RB);
scene.add(RBx);
scene.add(RBy);
scene.add(P);
scene.add(Pab);
scene.add(Pcd);
}
function Forces_Pos()
{ var DB = (1-controls.gamma) * controls.length1;
var DE = (controls.gamma - (-controls.PositionPab)) * controls.length1;
var AD = controls.gamma * controls.length1;
var CD = controls.length1 * controls.gamma * Math.sin(controls.alpha1)/Math.sin(controls.alpha2);
var DK = AD * Math.sin(controls.alpha1)
var DF = CD *(1- controls.PositionPcd);
var yC = ((-controls.Pab * DE + controls.P * DB +(controls.Pab+controls.Pcd+controls.P) * AD) * Math.cos(controls.alpha1) + controls.Pcd * DF * Math.cos(controls.alpha2))/(CD * Math.cos(controls.alpha2) + AD * Math.cos(controls.alpha1)) ;
var yA = controls.Pab + controls.Pcd + controls.P - yC;
var xA = (-yA * AD *Math.cos(controls.alpha1) + controls.Pab * DE * Math.cos(controls.alpha1) - controls.P * DB * Math.cos(controls.alpha1))/(AD * Math.tan(controls.alpha1));
var xC = -xA;
var Nbx = 1 * 1;
var Nay = 1 * Nbx;
var Ra = Math.sqrt(xA * xA + yA * yA);
var Rb = Math.sqrt(xC * xC + yC * yC);
var lp = controls.length1 * 1 * (1 + Math.tan(controls.alpha1)) / (1 + 1 * 1);
var headLength = 0.15;
var headWidth = 0.1;
var Xpab = controls.gamma * controls.length1 * Math.cos(controls.alpha1)-(1-controls.PositionPcd)*(controls.gamma * controls.length1 * Math.cos(controls.alpha1)-controls.gamma * controls.length1 * Math.sin(controls.alpha1) * Math.cos(controls.alpha2)/Math.sin(controls.alpha2))
Forces_Remove();
RA = new THREE.ArrowHelper(new THREE.Vector3(xA, yA, 0).normalize(), new THREE.Vector3(0, 0, 0), Ra, 0xFF0000, headLength, headWidth);
RAx = new THREE.ArrowHelper(new THREE.Vector3(-1, 0, 0), new THREE.Vector3(0, 0, 0), -xA, 0xFF0000, headLength, headWidth);
RAy = new THREE.ArrowHelper(new THREE.Vector3(0, 1, 0), new THREE.Vector3(0, 0, 0), yA, 0xFF0000, headLength, headWidth);
RB = new THREE.ArrowHelper(new THREE.Vector3(xC, yC, 0).normalize(), new THREE.Vector3(controls.gamma * controls.length1 * Math.sin(controls.alpha1) * Math.cos(controls.alpha2)/Math.sin(controls.alpha2), 0, 0), Rb, 0xFF0000, headLength, headWidth);
RBx = new THREE.ArrowHelper(new THREE.Vector3(1, 0, 0), new THREE.Vector3(controls.gamma * controls.length1 * Math.sin(controls.alpha1) * Math.cos(controls.alpha2)/Math.sin(controls.alpha2), 0, 0), xC, 0xFF0000, headLength, headWidth);
RBy = new THREE.ArrowHelper(new THREE.Vector3(0, 1, 0), new THREE.Vector3(controls.gamma * controls.length1 * Math.sin(controls.alpha1) * Math.cos(controls.alpha2)/Math.sin(controls.alpha2), 0, 0), yC, 0xFF0000, headLength, headWidth);
P = new THREE.ArrowHelper(new THREE.Vector3(0, -1, 0), new THREE.Vector3(controls.length1 * Math.cos(controls.alpha1), -controls.length1 * Math.sin(controls.alpha1), 0), controls.P, 0xFF0000, headLength, headWidth);
Pab = new THREE.ArrowHelper(new THREE.Vector3(0, -1, 0), new THREE.Vector3(controls.length1 * Math.cos(controls.alpha1)*controls.PositionPab, -controls.length1 * Math.sin(controls.alpha1)*controls.PositionPab, 0), controls.Pab, 0xFF0000, headLength, headWidth);
Pcd = new THREE.ArrowHelper(new THREE.Vector3(0, -1, 0), new THREE.Vector3( Xpab,controls.gamma*(-controls.length1 * Math.sin(controls.alpha1))*controls.PositionPcd, 0), controls.Pcd, 0xFF0000, headLength, headWidth);
Forces_Push();
}
function Refresh_Scene()
{
Stairs_Pos();
Forces_Pos();
}
function init()
{
scene = new THREE.Scene();
camera = new THREE.PerspectiveCamera(60, window.innerWidth/window.innerHeight, 0.1, 1000);
renderer = new THREE.WebGLRenderer();
renderer.setClearColor(0xEEEEEE, 1.0);
renderer.setSize(window.innerWidth, window.innerHeight);
var axes = new THREE.AxisHelper(20);
scene.add(axes);
Refresh_Scene();
camera.position.x = 0;
camera.position.y = 0;
camera.position.z = 10;
camera.lookAt(0, 0, 0);
document.getElementById("WebGL").appendChild(renderer.domElement);
controls1 = new THREE.OrbitControls(camera, renderer.domElement);
stats = initStats();
RenderScene();
};
function RenderScene()
{
stats.update();
requestAnimationFrame(RenderScene);
renderer.render(scene,camera);
}
function initStats()
{
stats = new Stats();
stats.setMode(0);
stats.domElement.style.position = '0px';
stats.domElement.style.left = '0px';
stats.domElement.style.top = '0px';
document.getElementById("Stats-output").appendChild(stats.domElement);
return stats;
}
window.onload = init; </script></body>