Решение задачи с бистабильной системой методом малого параметра
Материал из Department of Theoretical and Applied Mechanics
Версия от 20:52, 2 июня 2017; Specter1771 (обсуждение | вклад) (Добавлена статья "Решение задачи с бистабильной системой методом малого параметра")
Содержание
Формулировка задачи[править]
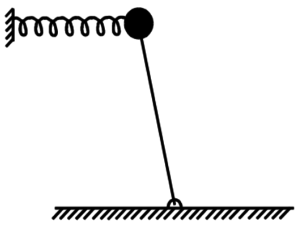
Рассматривается система, представляющая собой маятник в верхнем положении равновесия, прикрепленный к пружине.
- Показать, что если пружина линейна и её коэффициент жесткости k невелик, то положение равновесия неустойчиво.
- Показать, что если пружина нелинейная, то в системе возможна бистабильность — реализуются два положения устойчивого равновесия. Нелинейность пружины описывается соотношением F = kx + cx^3.
Презентация[править]
Визуализация решения задачи[править]