Численные эксперименты с параллельным программированием. Шубин Андрей. 6 курс
Цель работы
Наибольший интерес при применении технологии параллельных вычислений в решении различного рода задач представляет наблюдение и анализ убывания времени расчета при увеличении числа процессов. Зная эту характеристику можно определить, какой из различных методов решения задачи будет предпочтительней при заданных условиях. Основной целью данной работы стало параллельное вычисление двойного интеграла для произвольной функции и исследование сходимости точности и времени вычислений в зависимости от числа процессов, как пример использования средств параллельного програмирования на основе MPI, а также вычисление числа пи как площадь единичной окружности тем же методом.
Метод исследования
Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI - библиотека передачи сообщений, собрание функций на C/C++, облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).
Решение задачи
Для тестирования метода параллельного вычисления был взят двойной интеграл для функции заключенный в квадрат [(0,1);(0,1)]. При расчете указанного интеграла используется метод прямоугольников для двумерной задачи, изображение метода можно увидеть на рисунке 1.
Отрезок [0..1] разбивается на заданное количество интервалов: N = 1000, 5000 и 10000. Заданное количество интервалов распределяется между определенным количеством процессов. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. Суммируя результаты, полученные каждым отдельным процессом, мы получаем конечный результат.
Универсальность программного кода позволила тем же методом вычислить число пи как площадь единичной окружности.
Код программы: программа
Результаты
Вычислен определенный интеграл .
При числе разбиений N = 1000:
| Количество процессоров [pcs] | Время рассчета [sec] | Результат [-] | Абсолютная ошибка [-] |
|---|---|---|---|
| 1 | 18.348 | 0.2105614 | |
| 2 | 9.305 | 0.2105614 | |
| 4 | 4.905 | 0.2105614 | |
| 8 | 2.869 | 0.2105614 | |
| 16 | 14.258 | 0.2105614 |
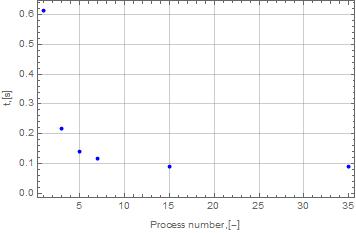
Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано - выигрыш во времени либо незначителен, либо же затраченное время увеличивается.