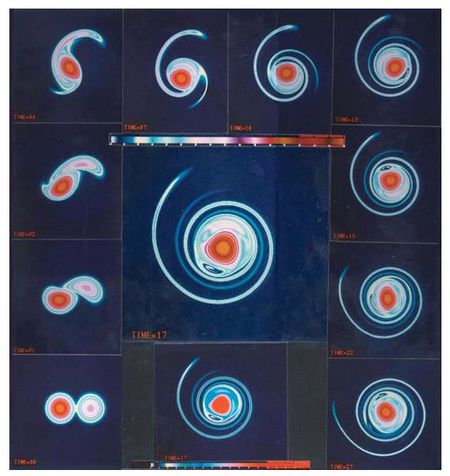
Обратный каскад энергии(двумерная турбулентность)

Рис.1 Взаимодействие двух вихрей.

Переход энергии с микро на макро уровень (и обратно) - одно из фундаментальных физических явлений. В данной работе,на примере двумерных турбулентных вихрей, рассматривается случай перехода с мелкомасштабного механического движения на крупномасштабное. В литературе это явление обычно упоминается как “обратный каскад” энергии. Построенная модель позволяет исследовать переход энергии с микро на макро уровень и корреляции скоростей в дискретной среде.

Модель представлена набором взаимодействующих частиц с случайными начальными скоростями. Частицы взаимодействуют за счет отталкивающих потенциальных и диссипативных сил. Динамика взаимодействия описана набором уравнений движения Ньютона:

[math]m\pmb{\ddot r}= \sum_{j}\left({{}^p}{\pmb F_{ij}} + {{}^d}{\pmb F_{ij}}\right),\qquad i,j = 1...N[/math]

где m, r - масса и радиус вектор i-ой частицы, [math]{{}^p}{\pmb F_{ij}}, {{}^d}{\pmb F_{ij}}[/math] - отталкивающая потенциальная и диссипативная силы соответственно.

Выражения для потенциальной и диссипативной сил:

[math] {{}^p}{\pmb F_{ij}} = \begin{cases} \frac{6D}{a^{2}}{\left(\frac{a_{c} - \pmb r_{ij}}{a_{c} - a}\right)}^{2}{\left(\frac{a}{\pmb r_{ij}}\right)}^{10}, & \text{если} \; \pmb r_{ij} \leqslant a_{c}; \\ 0, & \text{если} \; \pmb r_{ij} \gt a_{c}. \end{cases} [/math]

[math] {{}^d}{\pmb F_{ij}} = \begin{cases} \beta {\left(\frac{a_{c} - \pmb r_{ij}}{a_{c} - a}\right)}^{2} \left( \pmb v_{j} - \pmb v_{i}\right)\cdot \pmb e_{ij} \pmb e_{ij} , & \text{если} \; \pmb r_{ij} \leqslant a_{c}; \\ 0, & \text{если} \; \pmb r_{ij} \gt a_{c}. \end{cases} [/math]

где [math]\pmb r_{ij} =\pmb r_{i} - \pmb r_{j},\; \pmb e_{ij} = \frac{\pmb r_{ij}}{r_{ij}},\; a_{c}[/math] - радиус обрезания, [math]a, D[/math] - энергетические параметры системы, [math] \beta [/math] - коэффициент вязкости.

Диссипативные силы уменьшают полную энергию системы. Таким образом, без внешнего добавления энергии система перейдет в состояние равновесия. В данной модели энергия добавляется при помощи термостата Берендсена. Скорости частиц на каждом шаге по времени перемножаются на параметр [math] s [/math] :

[math] s = \sqrt{\frac{T_{0}}{T}},\qquad T =\frac{1}{2}\sum_{i} m {\pmb v_{i}}^{2} [/math]

где [math] T [/math] - температура среды

Программа

Частички расположены впритык друг к другу и образуют прямоугольную решетку. С помощью написанной программы можно изменять количество шаров, коэффициент вязкости и температуру в среде(термостат).

Текст программы на языке JavaScript:

Файл "Inverse cascade.js"

  1 // Версия 16.12.16
  2 
  3 function MainBalls(canvas, slider_01, text_01, slider_02, text_02) {
  4 
  5     canvas.onselectstart = function () {return false;};     // запрет выделения canvas
  6 
  7     // Предварительные установки
  8 
  9     var context = canvas.getContext("2d");                  // на context происходит рисование
 10     canvas.oncontextmenu = function (e) {return false;};    // блокировка контекстного меню
 11 
 12     var Pi = 3.1415926;                 // число "пи"
 13 
 14     var m0 = 1;                         // масштаб массы
 15     var T0 = 1;                         // масштаб времени (период колебаний исходной системы)
 16     var a0 = 1;                         // масштаб расстояния (диаметр шара)
 17 
 18     var C0 = m0 * k0 * k0;              // масштаб жесткости
 19     var B0 = 2 * m0 * k0;               // масштаб вязкости
 20 	
 21 	var G = 0;
 22 	var G1 = 0;
 23 	var G2 = 0;
 24 
 25     // *** Задание физических параметров ***
 26 
 27     var Ny = 30;                         // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
 28     var m = 1 * m0;                     // масса
 29     var Cwall = 10 * C0;                // жесткость стен
 30     var Cball = 0.1 * Cwall;            // жесткость между частицами
 31  
 32     var Bball = 0.01 * B0;              // вязкость между частицами
 33     var Bwall = 0.03 * B0;              // вязкость на стенках
 34     var r = 0.5 * a0;                   // радиус частицы в расчетных координатах
 35     var K = 0.7;                        // все силы, зависящие от радиуса, ограничиваются значением, реализующимся при r/a = K
 36     var a = 2 * r;                      // равновесное расстояние между частицами
 37     var aCut = 2 * a;                   // радиус обрезания
 38 
 39     // *** Задание вычислительных параметров ***
 40 
 41     var fps = 50;                       // frames per second - число кадров в секунду (качечтво отображения)
 42     var spf = 100;                      // steps per frame   - число шагов интегрирования между кадрами (скорость расчета)
 43     var dt  = 0.045 * T0 / fps;         // шаг интегрирования (качество расчета)
 44 	
 45     // Выполнение программы
 46 
 47     var r2 = r * r;                     // ___в целях оптимизации___
 48     var aCut2 = aCut * aCut;            // ___в целях оптимизации___
 49     var a2 = a * a;                     // ___в целях оптимизации___
 50     var D = a2 * Cball / 72;            // энергия связи между частицами
 51 	
 52 	var steps = 0;
 53 	var Temp = 0;
 54 	Temp0 = 0.12 * D;
 55 	var B1 = 12*Math.sqrt((2*D)/a2);
 56 	var B = 0.026 * B1;
 57 	var betta = 3.5*B;
 58 	var LJCoeff = 6 * D / a2;          // коэффициент для расчета потенциала Л-Дж
 59 	
 60     var Ka = K * a;                     // ___в целях оптимизации___
 61     var K2a2 = K * K * a2;              // ___в целях оптимизации___
 62 
 63     var dNd = null;                     // ссылка на захваченный курсором шар (drag & drop)
 64     var grad;                           // должен ли работать градиент (регулируется в функции setNy())
 65 
 66 	this.set_01 = function(p) {betta = p * B;};
 67 	this.set_02 = function(pT) {Temp0 = pT *D;};
 68 	
 69     this.setNy = function(ny) {
 70         Ny = ny;
 71         context.fillStyle = "#3070d0";  // цвет, шара
 72     };
 73     this.setNy(Ny);                         // запускаем с уже присвоенным значением, чтобы обновились настройки градиента
 74 
 75     // Запуск новой системы
 76 
 77     // следующие переменные должны пересчитываться каждый раз, когда мы изменяем значение Ny
 78     var scale, w, h;
 79     var rScale13, rScaleShift;
 80     this.newSystem = function() {
 81         scale = canvas.height / Ny / a0;    // масштабный коэффициент для перехода от расчетных к экранным координатам
 82         w = canvas.width / scale;           // ширина окна в расчетных координатах
 83         h = canvas.height / scale;          // высота окна в расчетных координатах
 84 
 85         rScale13 = r * scale * 1.3;         // ___в целях оптимизации___
 86         rScaleShift = r * scale / 5;        // ___в целях оптимизации___
 87 
 88       this.setMy();
 89     };
 90 
 91     // настройка слайдеров и текстовых полей
 92     slider_01.min = 0.1;               slider_01.max = 20;
 93     slider_01.step = 0.1;
 94     slider_01.value = betta / B;          // начальное значение ползунка должно задаваться после min и max
 95     text_01.value = betta / B;
 96 
 97 	// настройка слайдеров и текстовых полей
 98     slider_02.min = 0.1;               slider_02.max = 1;
 99     slider_02.step = 0.1;
100     slider_02.value = Temp0 / D;          // начальное значение ползунка должно задаваться после min и max
101     text_02.value = Temp0 / D;
102 	
103 	// график
104 	var vGraph1 = new TM_graph(                  // определить график
105 	"#vGraph1",                              // на html-элементе #vGraph
106 	20000,                                    // сколько шагов по оси "x" отображается
107 	0, 1,0.1);                            // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
108 	
109     // Работа с массивом
110 
111     var balls = [];                             // массив шаров
112     var addNewBall =  function(x, y, check) {
113         // проверка - не пересекается ли новый шар со стенами или уже существующими шарами
114         if (check) {
115             if (x - r < 0 || x + r > w || y - r < 0 || y + r > h) return null;
116             for (var i = 0; i < balls.length; i++) {
117                 var rx = balls[i].x - x;
118                 var ry = balls[i].y - y;
119                 var rLen2 = rx * rx + ry * ry;
120                 if (rLen2 < 4 * r2) return null;
121             }
122         }
123 		
124         var b = [];
125 
126         b.x = x;                b.y = y;        // расчетные координаты шара
127         b.fx = 0;               b.fy = 0;      // сила, действующая на шар
128         b.vx = (3 * (1 - 2 * Math.random()));               b.vy = (3 * (1 - 2 * Math.random()));       // скорость
129 
130        // balls[balls.length] = b;                // добавить элемент в конец массива
131 		balls.push(b);
132         return b;
133     };
134 	
135 	this.setMy = function() {
136 	  balls = [];
137         for (var j = 0; j < Ny; j++)
138             for (var i = 0; i < Ny; i++)
139 				addNewBall(w*j/Ny + r, h*i/Ny + r , true);                // задаем 50x50
140 		document.getElementById('ballsNum').innerHTML = balls.length;
141 	}
142 	
143     // Основной цикл программы
144 
145     function control() {
146         physics();
147         draw();
148     }
149 
150     // Расчетная часть программы
151 
152     function physics() {                        // то, что происходит каждый шаг времени
153         for (var s = 1; s <= spf; s++) {
154 
155 			for (var i0 = 0; i0 < balls.length; i0++) {
156                 Temp = 1/2 * (balls[i0].vx * balls[i0].vx + balls[i0].vy * balls[i0].vy) / Ny;
157 				var stat = Math.sqrt(Temp0/Temp);
158 				balls[i0].vx*=stat;
159 				balls[i0].vy*=stat;
160             }			
161             for (var i = 0; i < balls.length; i++) 
162 			{
163                 // расчет взаимодействия производится со всеми следующими шарами в массиве,
164                 // чтобы не считать каждое взаимодействие дважды
165                 var b = balls[i];
166                 for (var j = i + 1; j < balls.length; j++) {
167                     var b2 = balls[j];
168                     var rx = b.x - b2.x;   var ry = b.y - b2.y;         // вектор смотрит на первый шар (b)
169                     var r2 = rx * rx + ry * ry;                         // квадрат расстояния между шарами					
170                     if (r2 > aCut2) continue;                           // проверка на радиус обрезания
171                     var rLen = (Math.sqrt(r2));
172 
173                     // если расстояние между частицами мало, силы будут посчитаны для K * a
174                     if (r2 < K2a2) {
175                         if (rLen > 0.00001) {                           // проверка, чтобы избежать деления на 0
176                             rx = rx / rLen * Ka;
177                             ry = ry / rLen * Ka;
178                         }
179                         r2 = K2a2;
180                         rLen = Ka;                                      // корень K2a2
181                     }
182                     // сила взаимодействия
183                     var s2 = a2 / r2;         var s4 = s2 * s2;         // ___в целях оптимизации___
184 					var s8 = s4 * s4;
185 					var F = LJCoeff * s8 * s2 * ((aCut - rLen)/(aCut - a));          // сила взаимодействия Леннарда-Джонса
186 					
187 					var vx21 = b.vx - b2.vx;    var vy21 = b.vy - b2.vy;    // вектор смотрит на первый шар (b)
188 					var ex = rx / rLen;         var ey = ry / rLen;
189 					var v = vx21 * ex + vy21 * ey;
190 					F -= betta * ((aCut - rLen)/(aCut - a)) * v * (1/rLen);
191 									
192                     // суммируем силы
193                     var Fx = F * rx*dt;        var Fy = F * ry*dt;
194 					
195 					b.vx += Fx;        b.vy += Fy;
196 					b2.vx -= Fx;        b2.vy -= Fy;
197 
198 					G2 += b.vx * b2.vx + b.vy * b2.vy;
199 					G1 += 1;
200 					
201                 }
202 
203                 if (b.y + r > h) { b.vy += (-Cwall * (b.y + r - h) - Bwall * b.vy)*dt; }
204                 if (b.y - r < 0) { b.vy += -Cwall * (b.y - r) - Bwall * b.vy;}
205                 if (b.x + r > w) { b.vx += -Cwall * (b.x + r - w) - Bwall * b.vx; }
206                 if (b.x - r < 0) { b.vx += -Cwall * (b.x - r) - Bwall * b.vx; }
207 
208             }  
209 			for (var i0 = 0; i0 < balls.length; i0++) {
210                 balls[i0].x += dt * balls[i0].vx;
211                 balls[i0].y += dt * balls[i0].vy;
212             }
213 			
214 			G = G2 / G1 / 2/ Temp0/Ny;
215 			
216 			steps++;
217             if (steps % 200 == 0) {
218 			vGraph1.graphIter(steps, (G))}
219         }
220     }
221 
222     // Рисование
223     function draw() {
224         context.clearRect(0, 0, w * scale, h * scale);      // очистить экран
225         for (var i = 0; i < balls.length; i++){
226             var xS = balls[i].x * scale;           var yS = balls[i].y * scale;
227             if (grad) {
228                 // расчет градиента нужно проводить для каждого шара
229                 var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
230                 gradient.addColorStop(0, "#0000bb");
231                 gradient.addColorStop(1, "#44ddff");
232                 context.fillStyle = gradient;
233             }
234 
235             context.beginPath();
236             context.arc(xS, yS, r*scale, 0, 2 * Math.PI, false);
237             context.closePath();
238             context.fill();
239         }
240     }
241 
242     // Запуск системы
243     this.newSystem();
244 	/*for (var i0 = 0; i0 < balls.length; i0++) {     // задаем частицам случайные скорости
245         balls[i0].vx = (3 * (1 - 2 * Math.random()));
246         balls[i0].vy = (3 * (1 - 2 * Math.random()));
247     }*/
248 	if(!window.requestAnimationFrame){
249 	window.requestAnimationFrame = (function(){
250 		return window.webkitRequestAnimationFrame
251 			|| window.mozRequestAnimationFrame
252 			|| window.oRequestAnimationFrame
253 			|| window.msRequestAnimationFrame
254 			|| function(callback, element){window.setTimeout(callback, 1000 / fps);};
255 	})();
256 }
257     //setInterval(control, 1000 / fps);
258 
259 	function animate(){
260 		requestAnimationFrame(animate);
261 		control();
262 	}
263 	animate();
264 }

Анализ

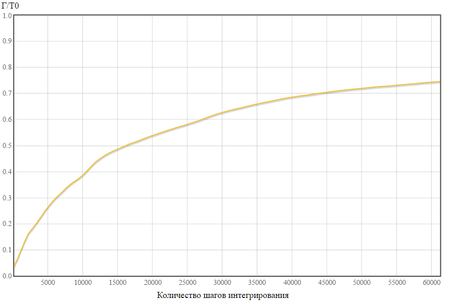
С помощью графика можно наблюдать за зависимостью корреляции скоростей [math] Г [/math] от входных параметров (вязкость, температура, кол-во частиц).

Уравнение для корреляции скоростей :

[math] Г= \frac{\sum_{i,j\neq i} m \pmb v_{i} \cdot \pmb v_{j} w\left(\pmb r_{ij}\right)}{2\sum_{i,j\neq i} w\left(\pmb r_{ij}\right) },\qquad w\left(r\right)= \begin{cases} 1, & \text{если} \; r \leqslant a_{c}; \\ 0, & \text{если} \; r \gt a_{c}. \end{cases} [/math]

Например, для начальной конфигурации на 60 000 шаге по времени будет наблюдаться график 1.

График 1. Начальная конфигурация:betta = 3.5 B; Temp0 = 0.12 D; Количество частиц:900 .

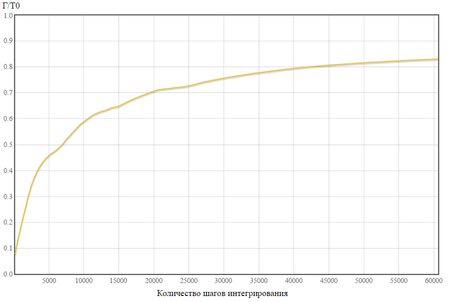
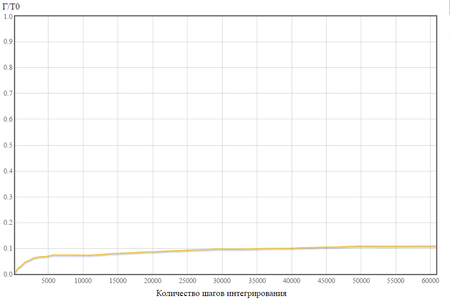
А для измененных входных параметров график 2 и 3.

График 2. Конфигурация:betta = 5 B; Temp0 = 0.12 D; Количество частиц:900 .

График 3. Конфигурация:betta = 1.5 B; Temp0 = 0.12 D; Количество частиц:900 .

Ссылки

• Vitaly A. Kuzkin, Anton M. Krivtsov. Interscale energy transport and velocity correlations in thermostated dissipative soft disc system.