Колебания материальной точки в поле силы тяжести
Материал из Department of Theoretical and Applied Mechanics
Виртуальная лаборатория > Колебания материальной точки в поле силы тяжести
Краткое описание системы
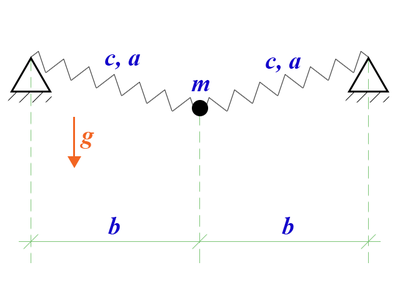
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами , длина пружин в недеформированном состоянии , жесткость пружин .
Уравнения движения системы будут выглядеть так:
Реализация
Ссылки
- Разработчик : Лобас Анна
- Виртуальная лаборатория
- Посмотреть код