Учет нелинейных эффектов при описании динамических процессов в полимерах

Учет нелинейных эффектов при описании динамических процессов в полимерах - научная работа, проводимая Витохиным Евгением на кафедре "Теоретическая механика" физико-механического факультета СПбГПУ под руководством Е.А. Ивановой.

Цель работы

В работах [1, 2, 3] предложена линейная теория термовязкоупругости, включающая уравнения теплопроводности гиперболического типа. Цель данной работы заключается в распространении этой теории на два случая нелинейности. Первый случай: учет нелинейной зависимости напряжений от механических деформаций. Второй случай: учет нелинейных тепловых эффектов.

Эксперимент

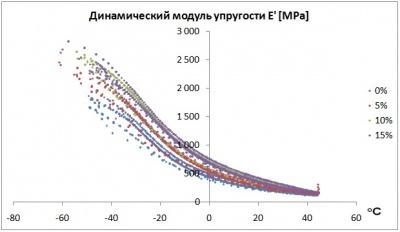
Учет нелинейности базируется на результатах экспериментальных исследований, проведенных в рамках научной работы на кафедре МСС и ВТ Пермского Государственного Университета. В ходе экспериментальной работы были получены зависимости динамического модуля упругости, модуля потерь и сдвига фаз от амплитуды перемещений в одной серии опытов, и от температуры в другой серии опытов. Выявлен нелинейный характер полученных зависимостей.

Динамический модуль упругости полиэтилена с различным процентом содержания глинистого нанонаполнителя в зависимости от температуры для частоты 0,1 Гц

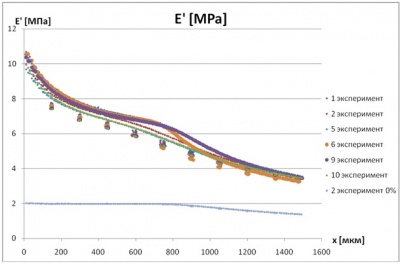
Динамический модуль упругости чистой резины и с 40% содержанием сажи при частоте 1Гц в зависимости от амплитуды перемещений

Аналитические зависимости

Выражая параметры теории термовязкоупругости, предложенной Ивановой Е.А., через экспериментальные данные, было получено следующее выражение для объемной вязкости:

[math]\eta_v=\frac{\lambda}{c_v}-\frac{1}{\omega}\left(\frac{E_2}{E_1}\right)\left(\frac{1}{E}-\frac{1}{E_1}\right)^{-1}[/math]

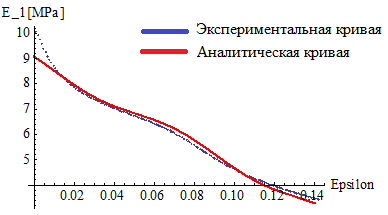
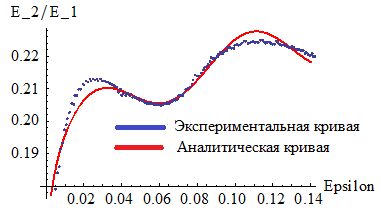
Таким образом задача свелась к аппроксимации зависимостей [math]E_1(\varepsilon)[/math] и [math]\frac{E_2}{E_1}(\varepsilon)[/math]. В итоге были получены следующие аналитические кривые:

Аналитическая кривая: [math]E_1=a_1\varepsilon+a_2\sin(\Omega_1\varepsilon-\varphi_1)+a_3[/math]

Аналитическая кривая: [math]\frac{E_2}{E_1}(\varepsilon)=b_1+b_2\ln(1+b_3\varepsilon)+b_4\sin(\Omega_2\varepsilon)[/math]

Нелинейные уравнения

В результате предложены нелинейные уравнения, описывающие поведение термовязкоупругих стержней, изготовленных из материалов типа полиэтилена, наполненного наночастицами, и углеродсодержащей резины

Текущая работа

В настоящее время ведется работа по численному решению полученных уравнений и сравнение результатов решения с аналитеческими данными.

Литература

1. Е.А. Иванова. Об одном подходе к формулировке связанной задачи термоупругости, включающей уравнение теплопроводности гиперболического типа //Пятые Поляховские чтения. Избранные труды. СПб. Изд. ВВМ. 2009. С. 301-306.
2. E.A. Ivanova. Derivation of theory of thermoviscoelasticity by means of two-component medium // Acta Mechanica: V. 215, Issue 1 (2010), P.261-286.
3. E.A. Ivanova. On one Model of Generalized Continuum and its Thermodynamical Interpretation // Proceedings of First German-French-Russian symposium on generalized continua. August 9 - 11, 2010, Lutherstadt Wittenberg, Germany. P.151-174.