Определение оптимальной конструкции кронштейна в условиях геометрической стесненности

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Т. А. Теницкая
Руководитель: аспирант кафедры ТМ О. В. Бразгина

Введение

Файл:DSC07945.png

Модель кронштейна

Нефтеперерабатывающий завод (НПЗ) представляет собой крупный промышленный комплекс, предназначенный для очистки сырой нефти, состоящий из большого количества оборудования различного назначения и размеров. Примером такого оборудования является ректификационная колонна. Такая колонна в диаметре может достигать 16 метров, а высотой – 90 метров и более. Для удобства обслуживания и ремонта колонны оборудуются по всей высоте маршевыми лестницами с площадками. Крепятся такие площадки, как правило, с помощью кронштейнов непосредственно к корпусу аппарата, обеспечивая доступ к люкам, штуцерам и установленной на них арматуре. В ситуациях, когда под кронштейном необходимо установить какое-либо оборудование или провести трубу, возникает проблема нагруженности оборудования весом обслуживающей площадки, а так же прочности самих элементов площадок. Одним из вариантов решения данной проблемы может быть подбор наиболее оптимальной конструкции кронштейнов, с помощью которых осуществляется крепление площадок к оборудованию.
Критерии оптимизации:

• напряжения и перемещения в балках кронштейна в пределах допустимых, указанных в СНиП 2.01.07.85 (при прочих равных)
• масса металлоконструкций должна быть минимальной
• нагрузки в точках опирания на корпус аппарата в пределах допустимых, не нарушающие его устойчивость

Цель работы

Оптимизация кронштейна в условиях геометрической стесненности в конечно-элементном пакете Ansys.

Задачи дипломной работы:

• решить задачу оптимизации конструкции кронштейна в условиях геометрической стесненности
• исследовать на устойчивость корпус оборудования при возможных вариантах конструкции кронштейна

Постановка задачи

Модель кронштейна

По рабочему чертежу была построена конечно-элементная модель кронштейна.Верхняя балка кронштейна представляет собой балку сечения 12П. Наклонная балка – уголок, размерами 90мм×7мм.
В качестве материала балок кронштейна была взята сталь С245
Е = 200 ГПа – модуль Юнга
υ = 0.3 – коэффициент Пуассона
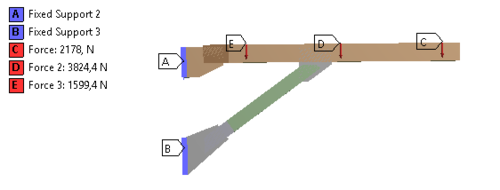
На пластины A и B поставлено условие заделки. К пластинам C, D, E приложены силы, рассчитанные из параметров площадки, равные 2178 Н, 3824.4 Н и 1599.4 Н соответственно. Пластины прикреплены к швеллеру и уголку болтами, которые позволяют элементам конструкции двигаться в стороны в промежутке [-1.5, 1.5] мм. Между пластинами и балками конструкции выставлен контакт с трением μ = 0.3.

Полученные результаты

Рассмотрим изменение напряжений в швеллере и уголке в зависимости от угла наклона уголка при различных высотах кронштейна.
Из соображений корректности геометрии кронштейна были выбраны три промежутка для высот и углов:
- для высоты кронштейна Н [700;1000] мм угол наклона подкоса α [30;45]°
- для высоты кронштейна Н [1000;1200] мм угол наклона подкоса α [35;45]°
- для высоты кронштейна Н [1200;1500] мм угол наклона подкоса α [40;45]°
В трех интервалах высот кронштейнов и углов наклона подкоса были выбраны оптимальные значения. Для интервалов [700;1000] мм и [30;45]° углы [35;40]° являются оптимальными параметрами. По промежуткам для высоты кронштейна [1000;1200] мм и угла наклона уголка [35;45] ° можно сказать, что оптимальный угол наклона - 39°. По третьему промежутку высот кронштейна [1000;1200] мм и углов наклона уголка [35;45]° оптимальными параметрами будут являться угол 43.5° .
Основания для таких выводов были получены исходя из графиков для напряжений в швеллере и уголке, перемещений и сил реакции опоры, действующей на кронштейн со стороны колонны. При подборе оптимальных параметров учитывались так же и количество материала, затрачиваемого на уголок.
Так же исследован на устойчивость корпус оборудования при одной фиксированной высоте кронштейна - 900 мм в интервале углов подкоса Колонна устойчива на всем промежутке, и с ростом угла устойчивость растет.

Вывод

Полученными результатами стали:

• поле скоростей;
• поле давлений;
• поле температур;

Полученные результаты могут быть использованы:

• для исследования оседания частиц в легких (мелкодисперсная пыль аэрозоли);
• моделирования полностью легких, включая альвеолы, как пороупругий материал;
• при создании искусственных легких.

Материалы работы

• Плакат (pdf)
• Плакат (png)
• Диплом (pdf)
• Превью (pdf)

Список литературы

1. Белебезьев, Г.И., Козяр, В.В.. Физиология и патофизиология искусственной вентиляции легких. Часть I - Ника-Центр, Киев, 2003
2. Белов, И.А., Исаев, С.А. Моделирование турбулентных течений Учеб. пособие. – СПб.: Балт. гос. техн. ун-т, 2001. –108 с.
3. Березовский, В.А., Колотилов, Н.Н. Биофизические характеристики тканей человека. Справочник. Киев, 1990.
4. Варламов, В.А., Варламов, Г.В., Власова, Н.М., Зубрилова, И.С., Котомин, М.Б. Углубленные кадровые проверки М. 2003
5. Гарбарук, А.В. Моделирование турбулентности в расчетах сложных течений: учебное пособие / А.В. Гарбарук, М.Х. Стрелец, М.Л. Шур – СПб: Изд-во Политехн. ун-та, 2012. – 88 с.
6. Злыгостев, А.С., Марченко, Т.О. Анатомия и физиология человека /Авторы-составители: Злыгостев А.С., Марченко Т.О. - Таганрог: http://anfiz.ru/, 2012
7. Книпович, Н. М. Бронхи Энциклопедический словарь Брокгауза и Ефрона: в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
8. Лагунова, И.Г. Трахео-бронхиальное дерево человека в период его роста (Анатомо-рентгенологическое исследование) / И.Г. Лагунова // Нарушения бронхиальной проходимости. — М., 1946. — С. 210.
9. Лойцянский, Л.Г. Механика жидкости и газа. - 7-е изд., испр. - М.: Дрофа, 2003. - 840 с.
10. Лукомский, Г.И. Атлас бронхоскопии / Г. И. Лукомский, В. А. Спасская. - М. : Медучпособие, 1965. - 90 с.
11. Неттер, Ф. Атлас анатомии человека: Уч. пос.-атлас / Под ред. Н.О. Бартоша; Пер. с англ. А.П. Киясова. – м.: гэотар-мед, 2003.
12. Орлов, Р.С. Нормальная физиология / Р.С. Орлов, А.Д. Ноздрачев.- М: ГЭОТАР-МЕД, 2005.
13. Роуч, П. Вычислительная гидродинамика. – М.: Мир, 1980. – 616с.
14. Сапин, М.Р. Анатомия человека, 2-х томах. М.: «Медицина», 2003 . – 992 с
15. Флетчер, К. Вычислительные методы в динамике жидкостей: В 2-х томах: Т. 1 и 2: Пер. с англ. – М.: Мир, 1991. – 504 с.
16. Devdatta, V.K.Katiyar, Pratibha, Sarita. Numerical simulation of flow structure and deposition of particles in Asthematic Airway Bifurcation/ Department of Mathematics, Indian Institute of Technology Roorkee, Uttrakhand, India, 2012.
17. Gihad Ibrahim. CFD models of the bronchial airways with dynamic boundaries/ Department of Engineering University of Leicester, Leicester, England, 2014.
18. ANSYS CFX-Solver Theory Guide ANSYS, Inc. 2009
19. http://cae-expert.ru/product/ansys-cfx
20. http://cae-club.ru
21. http://www.ansys.com/