Моделирование распространения колебаний в бесконечном теле методом конечных элементов
БАКАЛАВРСКАЯ РАБОТА
Автор работы: В. С. Погодина
Руководитель: ассистент кафедры ТМ С. А. Ле-Захаров
Содержание
Введение
Задачи геологоразведки, прогнозирование техногенной взрывной волны, расчет зданий и сооружений на действие сейсмических волн и другие динамические задачи распространения волн в твердом теле в настоящее время весьма актуальны. Целью данной работы является исследование распространения волн, возникающих под действием постоянной точечной силы, в бесконечных телах.В связи с поставленной целью в работе решаются следующие задачи:
- описать основные методы моделирования «бесконечных» границ
- выбрать подходящий способ моделирования «бесконечной» границы для одномерного и двумерного тела
- провести моделирование распространения волн в бесконечном одномерном и двумерном телах с помощью выбранных способов моделирования «бесконечных» границ
- проанализировать полученные результаты
Моделирование фиктивной неотражающей границы
Существует несколько подходов к решению задачи моделирования поглощающей границы. Здесь рассматриваются два основных: вязкие и вязкоупругие граничные условия.
Вязкие граничные условия
В однородных изотропных средах существует два типа волн:продольные и поперечные. Их скорости соответственно равны.
где - модуль сдвига, а - упругая константа, найденная по формуле:
где \mu - коэффициент Пуассона. Вязкие граничные условия задаются в соответствии с формулами, предложенными J. Lysmer и R. Kuhlemeyer:
Вязкие граничные условия в точности передают все нормально набегающие плоские волны тела. Для тех случаев, когда не удается добиться поглощения волны, используются вязкоупругие граничные условия.
Вязкоупругие граничные условия
Исходя из названия вязкоупругих граничных условий, очевидно, что они имеют вязкую и упругую составляющую. Данная модель приведена в работе Андервуда и Гирса. Вязкая состовляющая задается как для вязких граничных условий.Упругая составляющая напряжений в граничных условиях задается исходя из решения стационарной задачи для достаточно большой области с тем же типом нагрузки, что и в динамической задаче.
Таким образом уравнения на границе примут следующий вид:
Одномерная задача
Задача распространения колебаний в бесконечном теле может быть решена в одномерной, двумерной или трехмерной постановке. Изучение волн начнем с простейшего случая одномерного движения среды, когда все характеристики волны зависят от одной декартовой координаты, например координаты х. В данной работе исследуется поведение среды в случае точечной постоянной силы.
Постановка задачи
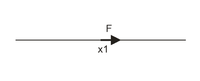
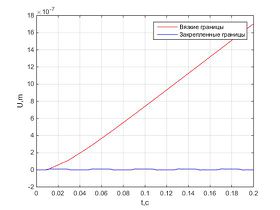
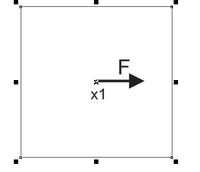
Имеется бесконечный стержень.Перемещения во всех точках этой прямой в начальный момент времени равны нулю.Начиная с момента времени, не равного нулю, в некоторой точке (х1) начинает действовать постоянная, сонаправленная с прямой сила F.Требуется найти зависимость перемещения от времени в любой точке прямой, в которой не приложена сила.Поглощающая граница создана с помощью вязких граничных условий.
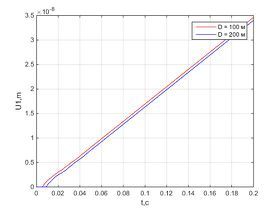
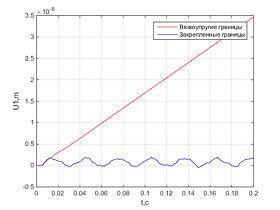
Результаты численного моделирования
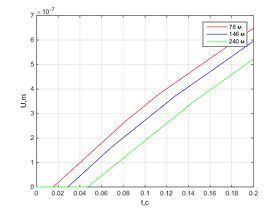
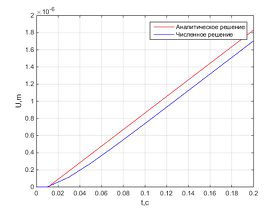
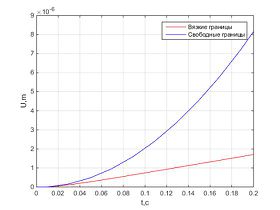
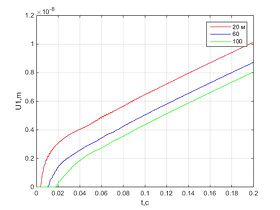
Было проведено численное решение и получены следующие результаты.Графики перемещения в разных точках стержня параллельны и отличаются лишь на длину участка, где перемещения нулевые.Численное решение незначительно отличается от аналитического, и ошибка не растет с течением времени.При использовании вязких граничных условий характер зависимости перемещения от времени линейный для всех точек стержня, в то время как для закрепленного стержня график перемещения колеблется возле некоторого значения, а для стержня со свободными границами – экспоненциально возрастает с течением времени.
Двумерная задача
Продолжим изучение волн с двумерного движения среды, когда все характеристики волны зависят от двух декартовых координат, например координаты х и у. В этом случае возникают два типа волн: продольные и поперечные. В этом случае мы сталкиваемся с проблемой задания таких граничных условий, которые поглощают эти два типа волн, а именно с вязкоупругими граничными условиями.
Постановка задачи
Имеется бесконечная плоскость.Начальные и граничные условия аналогичны одномерной задаче с отличием лишь в том, что они формулируются для двумерного случая. Перемещения во всех точках этой плоскости в начальный момент времени равны нулю. Начиная с момента времени, не равного нулю, в некоторой точке (х1) начинает действовать постоянная, сонаправленная, например, с осью абсцисс сила F. Требуется найти зависимость перемещения от времени в любой точке плоскости, в которой не приложена сила.
Результаты моделирования
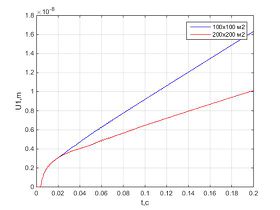
Было проведено численное моделирование и получены следующие результаты.Вязкие границы, реализованные с помощью «бесконечных» элементов или демпферов, не могут быть использованы для моделирования поглощающих границ, так как не поглощают весь спектр волн.Большое влияние на способность вязких границ проводить волны оказывает угол падения волны на границу.Вязкоупругие границы, реализованные с помощью демпферов и пружинок, чувствительны к воздействиям всего спектра частот, поэтому хорошо проводят волны на бесконечность.
Выводы
В ходе работы были решены сразу несколько задач:
1) Обработаны экспериментальные данные датчиков в плотине. Реализована схема отсеивания датчиков показывающие неразумные значения. А на показаниях хорошо работающих датчиков построены модели зависимостей порового давления от уровня УВБ.
2) Реализована модель пороупругого материала для бетона в вычислительном пакете SIMULIA ABAQUS. Получены результаты для различных постановок задачи. Проведено сравнение результатов от постановки задачи. Исследована зависимость порового давления от УВБ.
3) Исследовано влияние угловой координаты на показания датчиков. Определено, что на показания влияет лишь высота расположения датчика и расстояние до центра кривизны плотины.
4) Проведено сравнение исследуемой модели и экспериментальных данных для 33 секции плотины.
По результатам данной работы можно сделать несколько выводов.
Во-первых, для сравнения результатов моделирования и реального материала в исследуемой плотине находится недостаточное количество датчиков. Так же возникает проблема, что находящиеся в плотине датчики расположены группами, но не по всему телу плотины, а лишь в определённых областях. Отсюда возникает затруднения при анализе эксперимента и сравнении его с результатами моделирования, так что делать каких-то уверенных выводов нельзя. Для полной уверенности нужно либо больше датчиков, либо сравнение моделирования и эксперимента нужно проводить по показаниям других групп датчиков, например, расходометрам, наклономеров, деформометров. Кроме того, можно пользоваться лабораторным экспериментом, выполненным с керном, изъятым из тела плотины, и моделированием этого лабораторного эксперимента. Это одно из направлений дальнейшего исследования.
Во-вторых, данная модель согласуется с экспериментом. Особенно хорошо, она описывает область вблизи противофильтрационной завесы плотины. Здесь наблюдается количественное и качественное совпадение. Но имеются расхождения в отдалении от нее. Одним из вариантов доработки модели является более точное описание материала бетона. Например, замена постоянной пористости, на некую функции зависящую от различных параметров: координаты, напряжения, температуры и так далее. Еще одним из направлений развития является оценка напряженно – деформированного состояния сооружений под действием землетрясения с учетом рассмотренных факторов, в том числе влияния поровой жидкости. Особый интерес данной проблемой, вызван появлением во время землетрясения новых трещин в сооружении и фильтрации жидкости в них изменения свойств и параметров сооружений. Реализация этих направлений является дальнейшим планом развития работы.
Материалы работы
Литература
- К.С. Басниев, А.М. Власов, И.Н. Кочина, В.М. Максимов. Подземная гидравлика. Учебник для ВУЗов – 1986г. 306 с.
- J.F. Shao, Y. Jia, D. Kondo, A.S. Chiarelli. A coupled elastoplastic damage model for semi-brittle materials and extension to unsaturated conditions – 2004г.
- М.Н.Ваучский, Ю.В.Добрица, А.П.Смирнов О.И.Канинский К вопросу о фильтрационных характеристиках бетона – 1998г.
- Н.А. Вульфович, Л.А. Гордон, Н.И. Стефаненко. Арочно-гравитационная плотина Саяно – Шушенской ГЭС. Оценка технического состояния по данным натурных наблюдений – 2012г.
- Е.Л. Косарев. Методы обработки экспериментальных данных – М.: ФИЗМАЛИТ – 2008, 208 с.
- Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика – М.: ЮНИТИ-ЛАНА – 2001г. 656 с.
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. Кн. 1 / Пер. с англ. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1986г.– 366 с.
- M. A. Blot General Theory of Three-Dimensional Consolidation – 1940 г.
- Alan W. Bishop. The principle of the effective stress – 1960г.
- Clayton, C.R.I., Steinhagen, Muller, Steinhagin, H.M., Powrie, W., Terzaghi, K. and Skempton, A.W. Terzaghi's theory of consolidation and the discovery of effective stress. (Compiled from the work of K. Trzaghi and A.W. Skempton). Proceedings of the ICE - Geotechnical Engineering, 113, (4) – 1995г., 191-205.
- Simulia Abaqus Theory Manual 6.11 – 2011г.
- Г. Стренг, Дж. Фикс - Теория метода конечных элементов – 1973 г.