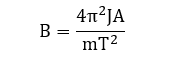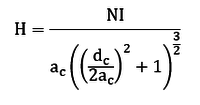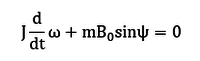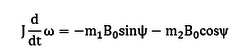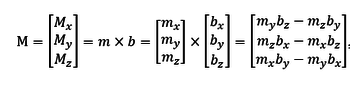Разработка системы ориентации и стабилизации малых космических аппаратов

Руководитель

А.С.Мурачев

Введение

Рис.1.CubeSat 1U

• Одной из самых важных задач при разработке космических аппаратов является создание системы

управления угловым движением. Работоспособность космических аппаратов существенным образом зависит от функциональных возможностей, а также технических и эксплуатационных характеристик этих систем. Особое место среди существующих систем управления занимают магнитные системы. Такие системы используют для получения управляющих моментов электромагнитные исполнительные органы, взаимодействующие с внешним магнитным полем. В магнитных системах управления в отличие от всех других систем легко изменять управляющие моменты и, следовательно, реализовывать самые разнообразные законы управления, что позволяет обеспечить точную ориентацию. Кроме этого, масса магнитных систем не зависит от продолжительности работы системы, в то время как энергопотребление системы незначительны. В магнитных системах также отсутствуют движущиеся элементы, в конструктивном отношении они просты и имеют высокую надежность. Все это позволяет космическим аппаратам долгосрочно выполнять свои функции.

Задачи

• Создание магнитной системы управления угловым движением КА.
• Разработка алгоритма управления при стабилизации КА по МПЗ.
• Создание имитатора поля.

Магнитное управление, принцип работы и особенности

Момент взаимодействия магнитной системы К.А с магнитным полем Земли (МПЗ):

Где: L – вектор магнитного момента К.А.; B – вектор индукции МПЗ.

Особенности магнитной системы управления

• Нельзя создать управляющий момент вдоль направления поля. Все возможные положения М заключены в плоскости, перпендикулярной В.
• Управление по осям оказывается зависимым.
• При совпадении вектора магнитного момента L и поля B управление невозможно

Принцип работы магнитной системы управления

• По принципу действия магнитная система демпфирования с катушечными и электромагнитными МИО – это по существу электродвигатель постоянного тока. В нем можно выделить все основные функциональные элементы: статор – это Земля, поле статора – МПЗ, ротор – КА, обмотки ротора – катушки МИО, коллектор – электронная часть системы, регулирующая и переключающая токи в МИЮ.
• Отличаются эти системы только режимом работы и «конструктивными» особенностями. Так, в отличие от классического электродвигателя рассматриваемый «двигатель» работает большей частью в режиме торможения; обычный режим двигателя бывает только, когда есть необходимость в увеличении скорости вращения КА. «Конструктивная» особенность состоит в том, что здесь используемся в некотором смысле обращенная конструкция: ротор – КА с МИО – находится не внутри статора, а вне его (Земли). Кроме того, «ротор» не фиксирован относительно «статора»: он совершает линейное движение относительно «статора», а также имеет три степени свободны и соответственно три системы обмоток (катушек МИО) – это как бы двигатель со сферическим ротором.
• Понятно, что энергетические соотношения, характерные для таких магнитных систем, будут такими же, как и для электродвигателей постоянного тока.

Создание имитатора поля

Напряженность поля

• Выполним оценку максимальной требуемой напряженности магнитного поля в данном случае. Для простоты определим параметры поля, чтобы механические моменты, действующие на макет, могли бы вынудить его совершать гармонические колебания.
• Требуемая индукция поля определяется следущим образом:

где Т - период колебаний, J - момент инерции макета, A – амплитуда колебания.

• Подставляя данные, получаем, что необходимая напряженность поля составляет H≈200 А/м. Если учитывать поправку на геомагнитное поле, то H надо увеличить еще на 50-100 А/м, чтобы надежно подавить геомагнитный фон. Таким образом получаем, что необходимая напряженность поля равна 250 А/м (~5 раз больше МПЗ).

Конструкция имитатора

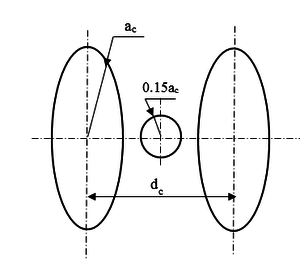
• Существуют различные геометрические конфигурации токовых катушек для создания однородное поле. Наиболее распространенней конфигурацей имитатора поля является "кольца Гельмгольца".Обозначим радиус катушки через а_с, расстояние между центрами катушек - d_c (рис.4). Показано [1][2], что оптимальной конфигурацией является та, для которой выполняется соотношение d_c⁄(a_c=1.116).

Рис.2.Кольца Гельмгольца

• Напряженность имитатора приблизительно можно выразить следующей формулой

Экспериментальный образец имитатора

Рис.3.Имитатор поля

Создание магнитной системы управления

Параметры токовых катушек

В работе проведен расчет параметров исполнительных орган (катушек)с целью минимизации потребляемой электроэнергии и массы системы управления. Получены следующие выводы:

• материалом катушки - медь,
• масса катушки M = 0.02 Кг,
• диаметр витка l = 0.1 м,
• площадь сечения материала обмотки должна быть равна S_r=0.0234мм^2, что соответствует диаметру d = 0.172 мм,
• напряжение на катушке равно 12 В,
• количество витков берем равным 240,
• длина катушки (в случае однослойной намотки) ,
• мощность каждой катушки W = 2 Вт.

Экпериментальные катушки

Рис.4.Макет спутника с токовыми катушками

• В соответствии с выбранными параметрами были созданы токовые катушки для спутника. Проволока, используемая для намотки катушек, была выбрана с диаметром 0.2 мм. Сопротивление каждой катушки R=N∙r=53.5 Ом. Измеряемое сопротивление каждой катушки составляет ≈55 Ом. То есть отклонение измеренного сопротивления от расчетного составляет ≈3 %. Такая разница может вызвана превышением числа витков в процессе ручной намотки. Используя формулы (20), получим создаваемый дипольный момент равен 0.42 Ам2. Относительное отклонение от требуемого значения момента составляет σ=5%. Разницы моментов и сопротивления катушек будут усчитаны при выводе закона управления системы. *Расположение двух катушек на макете спутника показано на рисунке справа.

Уравнение и закон управления движением спутника

Уравнение движения спутника

• Уравнение движения спутника относительно вертикальной оси запишется в следующем виде:

где: m – дипольный момент КА; ω – угловая скорость макета вокруг вертикальной оси; ψ – угол отклонения дипольного момента КА от вектора индукции МПЗ. J - момент инерции спутника относительно вертикальной оси

• Если спутник содержит две токовых катушки, его дипольный момент складывается из моментов двух катушек. Перепишем уравнение движения:

где: m1,m2 – дипольный момент первой и второй катушек соответственно; ψ – угол между моментом первой катушки и индукция МПЗ.

Закон управления

• Желаемый дипольный момент катушек определяется следующим образом:

m=Kp*e+Kd*de/dt + Ki∫de где: - Kp, Kd, Ki: пропорциональный, дифференцирующий интегральный коэффициенты, соответственно; - e="ψ"_желаемый-"ψ" : разность между желаемым и измеряемым углами.

• Для получения данного дипольного момента, необходимо приложить дипольные моменты вдоль двум остальным осям в соответствии с выражением:

где b = B/|B| - нормированный вектор индукции поля в связанной системе координат.

Эксперименты

Рис.5. ψ_желаемый=п/3

Рис.6. ψ_желаемый=2п/3

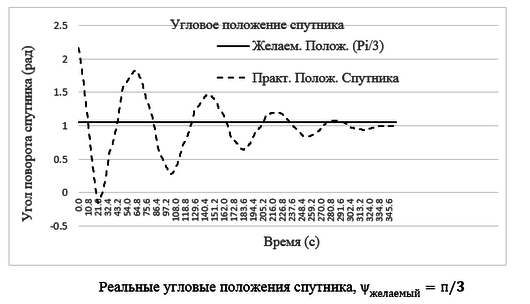
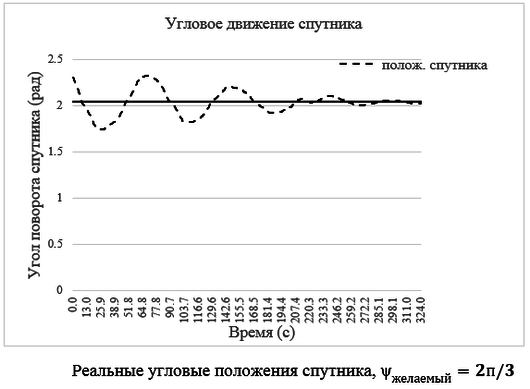
На рис.5 и рис.6 показаны графики реальных угловых положений спутника для разных заданных углов ψ_желаемый=п/3 и ψ_желаемый=2п/3 соответственно. Абсолютная ошибка ориентации спутника составляет 10 град. (~0.17 рад).

Выводы

• Изучен принцип магнитного управления малыми космическими аппаратами, подробно рассмотрены его особенности, достоинства и недостатки.
• Выбрана конструкция и проведены расчеты электрических, магнитных параметров, также создан имитатор геомагнитного поля.
• Проведены расчеты параметров токовых катушек и создана система магнитного управления спутника.
• Вывод уравнение движения спутника, построена математическая модель и проведено численное решение.
• Реализован закон управления спутника при стабилизации КА относительно МПЗ.

Литература

• 1. M.Pastena and M.Grassi, Optimum Design of a three-axis Magnetic Field Simulator, IEEE Transaction on Aerospace and Electronic Systems, Vol.38, No.2, April 2002, pp.488-501.
• 2. Коваленко А.П. Магнитные системы управления космическими летательными аппаратами. М., «Машиностроение», 1975, 248с.
• 3. Д.В.Сивухин. Общий курс физики. Учебное пособие: для вузов. В 5 т. Т.III. Электричество. 4-е изд., стереот. М.: Физматлит; Издательство МФТИ, 2002 г, 656 с.
• 4. Айзерман М.Ф. Классическая механика. «Наука» Изд.; М, 1980г, 368 с.
• 5. Овчинников М.Ю., Цветков Е.А. Москва, 2005 Проектирование имитатора геомагнитного поля в составе лабораторного стенда для отработки способов управления ориентацией микроспутников.
• 6. П.Л.Калантаров, Л.А.Цейтлин. Расчет индуктивностей: Справочная книга. 3-е изд., переработанное и дополненное. Л.: Энергоатомиздат, Ленинградское отделение, 1986 г, 488 с.
• 7. Active magnetic control system for gravity gradient stabilized spacecraft. Francois Martel, Parimal K.Pal and Mark Psiaki, Cornell University
• 8. Control systems, robotics and automation - Vol. II - PID Control - Araki M.
• 9. Севастьянов Н.Н., Бранец В.Н., Панченко В.А., Казинский Н.В., Кондрации Т.В., Негодяцев С.С. Анализ современных возможностей создания малых космических аппаратов для дистанционного зондирования Земли. Труды МФТИ No3, том 1. -2009.
• 10. Гущин В.Н. Основы устройства космических аппаратов. ¬ М.: Машиностроение, 2003.
• 11. Ziegler, J.G & Nichols, N. B. (1942). "Optimum settings for automatic controllers". Transactions of the ASME 64.
• 12. Euston, M.; Coote, P.; Mahony, R.; Kim, J.; Hamel, T. A complementary filter for attitude estimation of a fixed-wing UAV. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Acropolis Convention Center, Nice, France, 22–26 September 2008.