Информатика: Движение тела в среде
Лебедев Станислав Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Скачать можно тут.
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Визуализированный результат работы программы
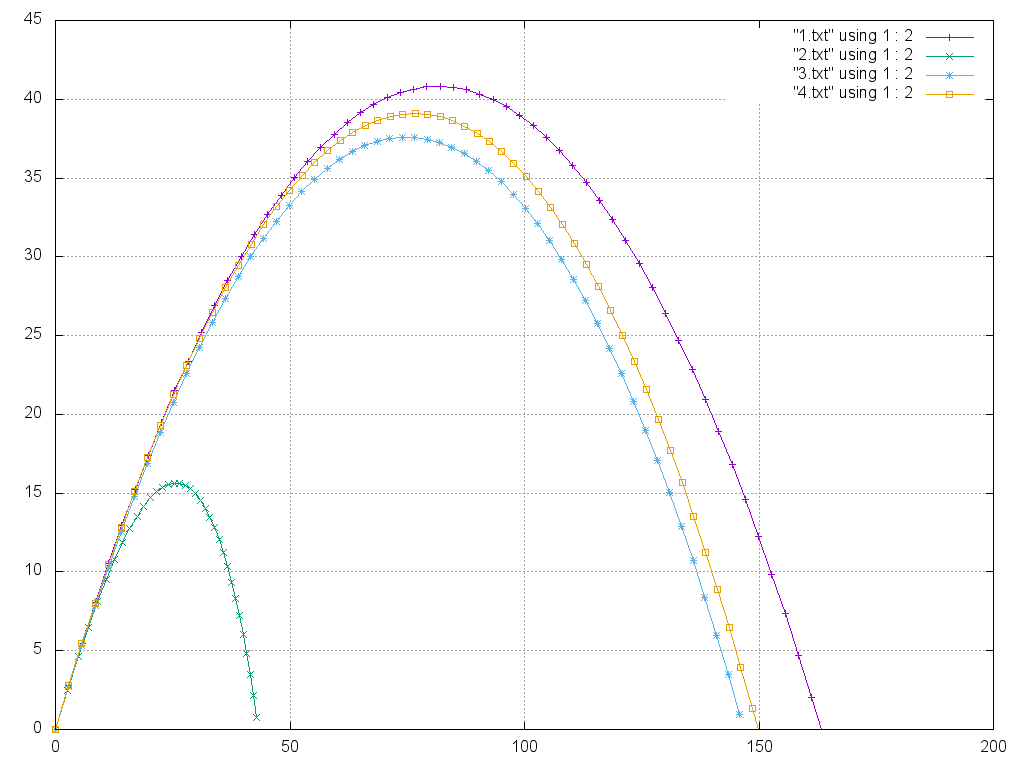
- o1 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- o2 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- o3 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- o4 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Для тела с массой 10,сопротивлением воздуха 1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2;
Примечание: графики o1 и o2 намеренно посчитаны с малой точностью, чтобы графики не сливались.
1 #include <iostream>
2 #include <math.h>
3 #include "Vector.h"
4 #include <cstring>
5 #include <cmath>
6 #include <malloc.h>
7 #include <fstream>
8
9 #include <iostream>
10 #include <math.h>
11 #include "Vector.h"
12 #include <cstring>
13 #include <cmath>
14 #include <malloc.h>
15 #include <fstream>
16
17 using namespace std;
18
19 int n = 100;
20 ofstream outfile;
21
22 class Ball //класс бросаемого тела
23 {
24 private:
25 double angle,m,k; //угол броска,масса,коэффицент сопротивления воздуха
26 Vector3D r,v,a; //радиус-вектор,вектор скорости,ускорения
27 public:
28
29 //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха
30 Ball(double _angle, Vector3D _r, Vector3D _v, Vector3D _a)
31 {
32 angle = _angle;
33 r = _r;
34 v = _v;
35 a = _a;
36 }
37
38 //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха
39 Ball(double _angle, double _m, double _k, Vector3D _r, Vector3D _v, Vector3D _a)
40 {
41 angle = _angle;
42 r = _r;
43 v = _v;
44 a = _a;
45 m = _m;
46 k = _k;
47 }
48
49 //точная формула зависимости координаты от времени
50 Vector3D positionReal(double t)
51 {
52 double c1 = m/k,c2 = fabs(a.y)*c1, c3 = exp(-t/c1), c4 = c2*t;
53 return MakeVector(v.x*c1*(1 - c3), c1*(v.y + c2)*(1 - c3) - c4 , 0 );
54 }
55
56 //вывод положения на экран
57 void writePosToScreen()
58 {
59 cout << r.x << " " << r.y << " " << r.z << endl;
60 }
61
62 //вывод положения в файл
63 void writePosToFile(char s[])
64 {
65 outfile.open(s,ios :: app);
66 outfile << r.x << " " << r.y << endl;
67 outfile.close();
68 }
69
70 //вывод произвольного вектора на экран
71 void WVTS(Vector3D v)
72 {
73 cout.width(15);
74 cout << v.x;
75 cout.width(15);
76 cout << v.y;
77 cout.width(15);
78 cout << v.z << endl;
79 }
80
81 //вывод произвольного вектора в файл
82 void WVTF(Vector3D v,char s[])
83 {
84 outfile.open(s,ios :: app);
85 outfile << v.x << " " << v.y << endl;
86 outfile.close();
87 }
88
89 //"пересчет" координаты по Верле(Линейная зависмость)
90 void changeR(Vector3D r1, double dt)
91 {
92 r = MakeVector(2 * r.x - r1.x - k/m*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*v.y)*dt*dt, 0 );
93 }
94
95 //"пересчет" координаты по Верле(Квадратичная зависимость)
96 void changeRSQ(Vector3D r1, double dt)
97 {
98 r = MakeVector(2 * r.x - r1.x - k/m*Length(v)*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*Length(v)*v.y)*dt*dt, 0 );
99 }
100 //пересчет скорости по Верле
101 void changeV(Vector3D r1,double dt)
102 {
103 v =VS((VmV(r,r1)),1/(2*dt));
104 }
105
106 //рассчет предыдущегт к 0ому элементу
107 Vector3D MR1(double dt)
108 {
109 return MakeVector(r.x - v.x * dt,r.y - v.y * dt,0);
110 }
111
112 //возращает координату тела
113 Vector3D getR()
114 {
115 return r;
116 }
117
118 //рассчет времени полета
119 double TimeOfFly()
120 {
121 return (2*Length(v)*sin(angle)/Length(a));
122 }
123
124 //рассчет координаты по точной формуле. без сопротивления воздуха.
125 Vector3D position(double t)
126 {
127 return MakeVector(r.x + v.x*t + a.x*t*t/2,r.y + v.y*t + a.y*t*t/2,r.z + v.z*t + a.z*t*t/2);
128 }
129
130 };
131
132 int main()
133 {
134 //задание начальных параметров
135 Vector3D g = {0,-9.8,0};
136 double a,dt = 0;
137 char s[20];
138
139 // cin >> dt;
140
141 dt = 0.1;
142 a = (M_PI * 30)/180;
143 Ball b1(a, MakeVector(0,0,0),MakeVector(30,a),g);
144
145 double tof = b1.TimeOfFly()+1; //единичка прибавлена,чтобы график красивым был
146
147 //Без сопротивления возлуха
148 strcpy(s,"");
149 strcat(s, "o1.txt");
150 outfile.open(s, ios :: trunc);
151 outfile.close();
152 for (double i = 0; i <= tof; i += dt)
153 {
154 b1.WVTS(b1.position(i));
155 b1.WVTF(b1.position(i), s);
156 }
157
158
159 //Верле(Линейная зависимость)
160 dt = 0.1;
161 a = (M_PI * 30)/180;
162 Ball b2(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
163
164 strcpy(s,"");
165 strcat(s, "o2.txt");
166 outfile.open(s,ios :: trunc);
167 outfile.close();
168 Vector3D r1 = b2.MR1(dt),rp;
169 for (double i = 0; i <= 20; i += dt)
170 {
171 rp = b2.getR();
172 b2.writePosToFile(s);
173 b2.writePosToScreen();
174 b2.changeR(r1,dt);
175 b2.changeV(r1,dt);
176 r1.x = rp.x;
177 r1.y = rp.y;
178 }
179
180 //Точное решение (Линейная зависимость)
181 dt = 0.1;
182 a = (M_PI * 30)/180;
183 Ball b3(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
184
185 strcpy(s,"");
186 strcat(s, "o3.txt");
187 outfile.open(s, ios :: trunc);
188 outfile.close();
189 for (double i = 0; i <= 20; i += dt)
190 {
191 b3.WVTS(b3.positionReal(i));
192 b3.WVTF(b3.positionReal(i), s);
193 }
194
195
196 //Верле (Квадратичная зависимость)
197 dt = 0.1;
198 a = (M_PI * 30)/180;
199 Ball b4(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
200
201 strcpy(s,"");
202 strcat(s, "o4.txt");
203 outfile.open(s, ios :: trunc);
204 outfile.close();
205 r1 = b4.MR1(dt);
206 for (double i = 0; i <= 20; i += dt)
207 {
208 rp = b4.getR();
209 b4.writePosToFile(s);
210 b4.writePosToScreen();
211 b4.changeRSQ(r1,dt);
212 b4.changeV(r1,dt);
213 r1.x = rp.x;
214 r1.y = rp.y;
215 }
216
217 return 0;
218 }
Белоусова Екатерина
Описание программы: пользователь вводит начальную скорость полета, угол бросания и шаг, с которым будут рассчитаны точки.
Программа записывает в один файл результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
Скачать можно тут.

Визуализированный результат работы программы
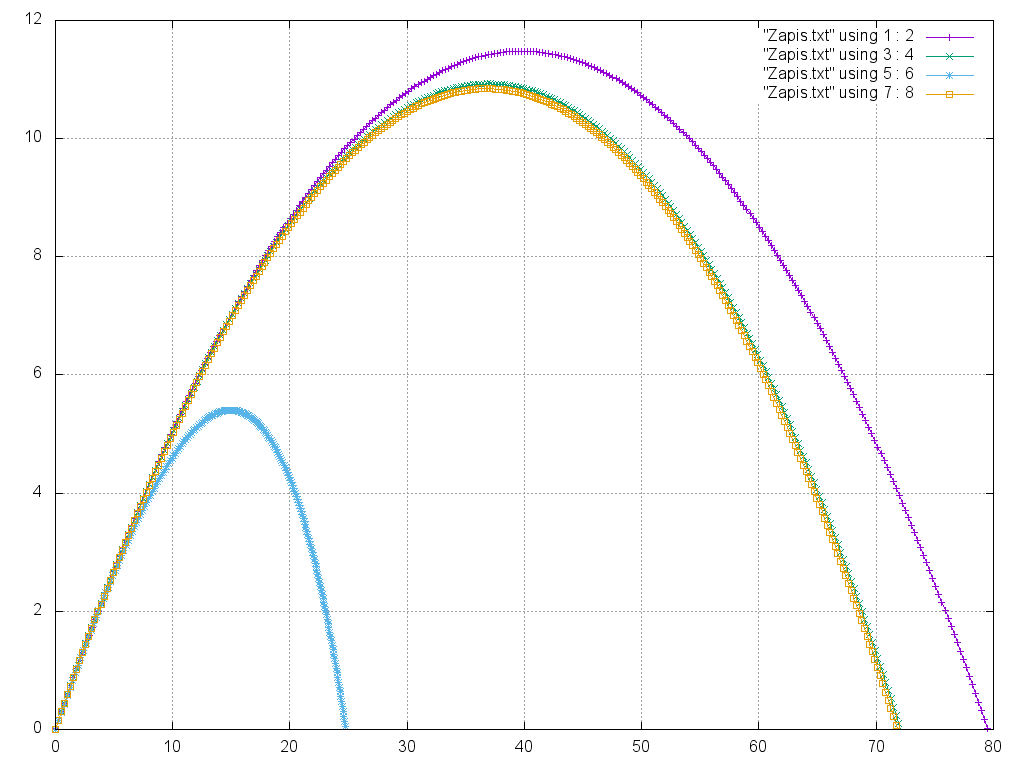
Для тела с массой 1 кг,сопротивлением воздуха 0.05, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.01;
- "Zapis.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- "Zapis.txt" using 3 : 4 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- "Zapis.txt" using 5 : 6 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости;
- "Zapis.txt" using 7 : 8 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости.
1 #include <iostream>
2 #include <locale.h>
3 #include <math.h>
4 #include <fstream>
5 #include<iomanip>
6 #include <cmath>
7
8 using namespace std;
9
10 class fly ///создаем класс полета тела
11 {
12
13 private: ///объявляем тип переменных в привате
14 double Vo, Agrad, Brad, time, step, amountdouble; ///Vo-начальная скорость тела; Agrad-угол, под которым летит тело, в градусах;
15 ///Brad-угол, под которым летит тело, в радианах; time-время полета тела; step-шаг;
16 ///amountdouble-количество точек (типа double)
17
18 public: ///объявляем переменные в паблике
19 int amount; ///amoun-количество точек (типа int)
20
21 fly (double _step, double _Agrad, double _Vo):step(_step),Agrad(_Agrad),Vo(_Vo) ///создаем конструктор функции с объявлением переменных
22 {
23
24 double g=9.8; ///объявляем тип и значение переменной g(ускорение свободного падения)
25 Brad=3.14159*Agrad/180.0; ///переводим значение угла из градусов в радианы
26
27 time=2*Vo*sin(Brad)/g; ///расчитываем время полета тела
28 amountdouble=(round(time/step)+1); ///подсчитываем количество точек с заданым шагом
29 amount=static_cast<int>(amountdouble); ///преобразуем количество из типа double к типу int
30
31 }
32 void zapis (char Zapis[]) ///создаем функцию записи
33 {
34 double g=9.8, m=1, n=0.05; ///объявляем тип и значения переменных g (ускорение свободного падения), m (масса тела), n(коэффициэнт сопротивления)
35 double Xb, Yb; ///объявляем тип переменных для полёта тела без сопротивления ветра Xb(координата тела по Х), Yb(координата тела по У)
36 double V=Vo, Vxv=Vo*cos(Brad), Vyv=Vo*sin(Brad), Xo=0, Yo=0, Xv=0, Yv=0, Y_1=Yo-Vo*sin(Brad)*step, X_1=Xo-Vo*cos(Brad)*step, Y=0, X=0;
37 ///объявляем тип переменных для метода ВерлеI V (скорость тела по модулю), Vxv (составляющая скорости по Х),
38 ///Vyv (составляющая скорости по У), Xo (начальное положение тела на оси Х), Yo (начальное положение тела на оси У),
39 ///Xv (координата тела на оси Х), Yv (координата тела на оси У), Y_1 (координата тела на (n-1)ом шаге на оси У),
40 ///X_1 (координата тела на (n-1)ом шаге на оси Х), Y (координата тела на n-ом шаге на оси У),
41 ///X (координата тела на n-ом шаге на оси Х);
42 double Vxv2=Vo*cos(Brad), Vyv2=Vo*sin(Brad), Xo2=0, Yo2=0, Xv2=0, Yv2=0, Y_12=Yo2-Vo*sin(Brad)*step, X_12=Xo-Vo*cos(Brad)*step, Y2=0, X2=0;
43 ///объявляем тип переменных для метода ВерлеII V (скорость тела по модулю), Vxv (составляющая скорости по Х),
44 ///Vyv (составляющая скорости по У), Xo (начальное положение тела на оси Х), Yo (начальное положение тела на оси У),
45 ///Xv (координата тела на оси Х), Yv (координата тела на оси У), Y_1 (координата тела на (n-1)ом шаге на оси У),
46 ///X_1 (координата тела на (n-1)ом шаге на оси Х), Y (координата тела на n-ом шаге на оси У),
47 ///X (координата тела на n-ом шаге на оси Х);
48 double Yt=0, Xt=0, Yot=0, Xot=0, Voxt=Vo*cos(Brad), Voyt=Vo*sin(Brad);
49
50 ofstream outfile("Zapis.txt"); ///запись элементов функции в фаил "Zapis.txt"
51 outfile<<setw(20)<<"Xb"<<setw(20)<<"Yb"<<setw(20)<<"Xt"<<setw(20)<<"Yt"<<setw(20)<<"Xv"<<setw(20)<<"Yv"<<setw(20)<<"Xv2"<<setw(20)<<"Yv2"<<" \n"; ///вывод на экран по столбцам
52 ///X (координата тела на оси Х без ветра),
53 ///Y (координата тела на оси У без ветра),
54 ///Xv (координата тела на оси Х с ветром для метода Верле),
55 ///Yv (координата тела на оси У с ветром для метода Верле)
56 ///setw() размер столбиков
57
58 for (int l=0; Yb>=0; ++l) ///создаем цикл от 0 до тех пор пока У больше нуля
59 {
60 outfile<<setw(20)<<Xb<<setw(20)<<Yb<<setw(20)<<Xt<<setw(20)<<Yt<<setw(20)<<Xv<<setw(20)<<Yv<<setw(20)<<Xv2<<setw(20)<<Yv2<<" \n";
61 ///вывод на экран по столбцам Xv, Yv;
62
63 ///полёт без ветра
64 Xb=Vo*cos(Brad)*l*step;
65 Yb=Vo*sin(Brad)*l*step-(9.8*l*step*l*step*0.5);
66
67 ///точный метод
68 Xt=Xot+(m/n)*Voxt*(1.0 - exp((-n*l*step)/m));
69 Yt=Yot+(m/n)*(Voyt+g*(m/n))*(1.0 - exp((-n*l*step)/m))-g*l*step*(m/n);
70
71 ///метод Верле I
72 Xv=2*X-X_1-(n/m)*V*Vxv*step*step; ///расчитываем координату Х в момент времени t для метода Верле
73 Yv=2*Y-Y_1-(g+(n/m)*V*Vyv)*step*step; ///расчитываем координату У в момент времени t для метода Верле
74 Vxv=(Xv-X_1)/(2.0*step); ///расчитываем скорость тела по оси Х в момент времени t для метода Верле
75 Vyv=(Yv-Y_1)/(2.0*step); ///расчитываем скорость тела по оси У в момент времени t для метода Верле
76 V=sqrt(Vxv*Vxv+Vyv*Vyv); ///рассчитываем скорость тела по модулю
77 X_1=X; ///присваиваем значению координаты Х на (n-1)ом шаге значение координаты Х на n-ом шаге
78 X=Xv; ///присваиваем значению координаты Х на n-ом шаге значение координаты Х
79 Y_1=Y; ///присваиваем значению координаты У на (n-1)ом шаге значение координаты У на n-ом шаге
80 Y=Yv; ///присваиваем значению координаты У на n-ом шаге значение координаты У
81
82 ///метод Верле II
83 Xv2=2*X2-X_12-(n/m)*Vxv2*step*step; ///расчитываем координату Х в момент времени t для метода Верле
84 Yv2=2*Y2-Y_12-(g+(n/m)*Vyv2)*step*step; ///расчитываем координату У в момент времени t для метода Верле
85 Vxv2=(Xv2-X_12)/(2.0*step); ///расчитываем скорость тела по оси Х в момент времени t для метода Верле
86 Vyv2=(Yv2-Y_12)/(2.0*step); ///расчитываем скорость тела по оси У в момент времени t для метода Верле
87 X_12=X2; ///присваиваем значению координаты Х на (n-1)ом шаге значение координаты Х на n-ом шаге
88 X2=Xv2; ///присваиваем значению координаты Х на n-ом шаге значение координаты Х
89 Y_12=Y2; ///присваиваем значению координаты У на (n-1)ом шаге значение координаты У на n-ом шаге
90 Y2=Yv2; ///присваиваем значению координаты У на n-ом шаге значение координаты У
91
92 }
93
94 outfile.close();
95
96 }
97
98 };
99
100 int main()
101 {
102
103 setlocale(LC_ALL,"RUS"); ///функция, позволяющая с++ распознавать русский язык
104
105 double Vo, Agrad, Brad, time, step; ///объявляем тип переменных Vo (начальная скорость тела), Agrad (угол, под которым летит тело, в градусах);
106 ///Brad (угол, под которым летит тело, в радианах); time (время полета тела); step (шаг)
107 cout<<"Задайте начальную скорость тела в м/с: Vo="; ///на экран выводится сообщение с просьюой задать начальную скорость тела
108 cin>>Vo; ///пользователь вводит начальную скорость тела
109 cout<<'\n'<<"Задайте в градусах угол, под которым брошено тело (угол должен принимать значения от 0 до 90): a=";
110 ///на экран выводится сообщение с просьбой задать угол, под которым летит тело, в градусах
111 cin>>Agrad; ///пользователь вводит угол, под которым летит тело
112 cout<<'\n'<<"Задайте шаг (шаг должен быть очень маленьким): шаг="; ///на экран выводится сообщение с просьбой ввести шаг
113 cin>>step; ///пользователь вводит шаг
114
115 fly X(step,Agrad,Vo); ///объявление коструктора, создание функции Х, зависящей от step,Agrad,Vo
116 X.zapis("координаты.txt"); ///запись элементов функции в файл
117
118 return 0; ///конец программы
119
120 }
Васильева Анастасия
Описание программы: пользователь вводит начальную скорость полета, угол бросания и шаг, с которым будут рассчитаны точки.
Программа записывает в один файл результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости (численное интегрирование - метод Эйлера);
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
Скачать можно тут.

Визуализированный результат работы программы
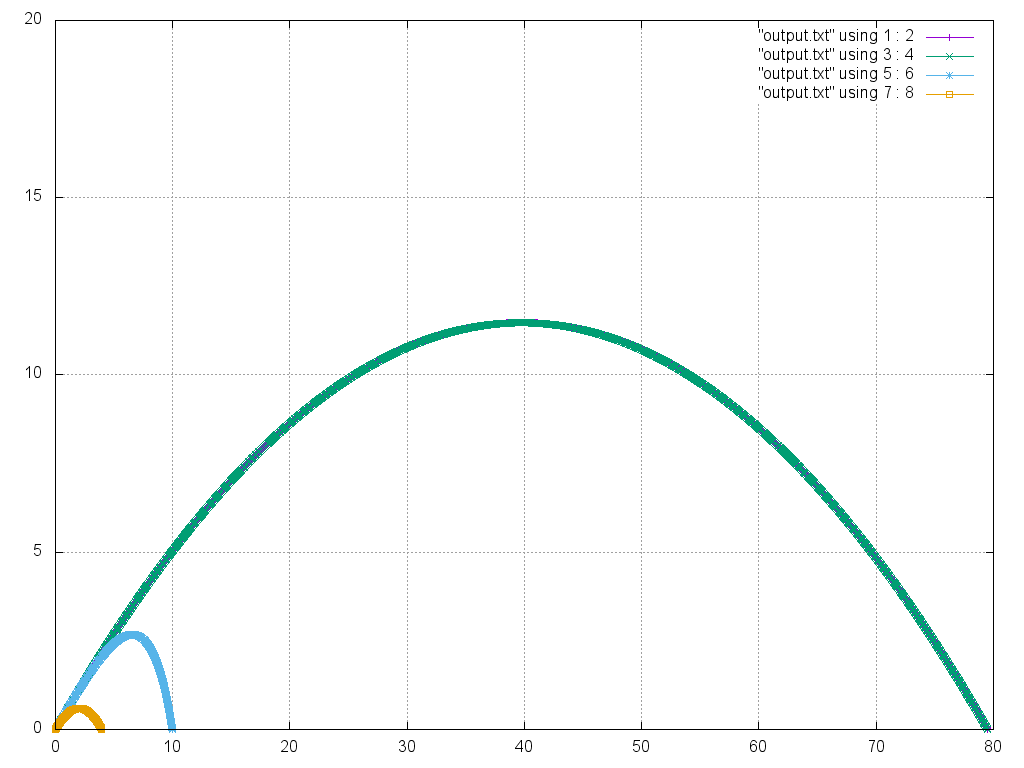
Для тела с массой 0.5 кг,сопротивлением воздуха 0.1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.001;
- "output.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- "output.txt" using 3 : 4 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости (численное интегрирование - метод Эйлера);
- "output.txt" using 5 : 6 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости;
- "output.txt" using 7 : 8 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости.
1 #include <iostream>
2 #include <fstream>
3 #include <iomanip>
4 #include <time.h>
5 #include <conio.h>
6 #include <stdlib.h>
7 #include <math.h>
8 #include <cstring>
9 using namespace std;
10
11 class pad ///создаем класс
12 {
13 private: ///в закрытом доступе
14 double *X, *Y, *E, *G, *Z, *S, *V, *U; ///координаты по х и у; *E, *G : численное интегрирование метод Эйлера, *Z, *S- метод верле, *V, *U- last verle
15 double a, g , pi;///ускорение, коэфф свободного падения, значение числа пи
16 int Size; ///размер массива- сколько точек считать в первом способе
17 double v, shag, b, vx, vy;///скорость, шаг по времени, угол в градусах скорость по х, скорость по у
18
19 void SetX() ///создаем функцию для вычисления значенй по х для простого падения и по эйлеру
20 {
21 g = 9.8;///коэфф свободного падения
22 float t = 0; ///время
23 X = new double [Size];///создаем массив для координат по х для простого падения
24 E = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру
25 X[0] = 0; ///задаем значение по х в нуле
26 E[0] = 0 ; ///задаем значение по х в нуле по эйлеру
27 for (int i = 1; i < Size; i++) ///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты
28 {
29 t += shag; ///каждый раз прибавляем по времени шаг
30 X[i] = v * cos(a) * t; ///координаты по х для простого падения
31 E[i] = E[i-1] + v * cos(a) * shag; ///х из интегрирования по эйлеру
32 }
33 }
34
35 void SetY()///создаем функцию для вычисления значенй по у для простого падения и по эйлеру
36 {
37 g = 9.8; ///коэфф свободного падения
38 double Vy; /// переменная для значение скорости по у для метода эйлера
39 float t = 0; ///время
40 Y = new double [Size];///создаем массив для координат по у для простого падения
41 G = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру
42 Vy = v * sin (a);/// значение скорости по у для метода эйлера
43 Y[0] = 0;///задаем значение по у в нуле
44 G[0] = 0;///задаем значение по у в нуле по эйлеру
45 for (int i = 1; i < Size; i++)///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты
46 {
47 t += shag; ///каждый раз прибавляем по времени шаг
48 Y[i] = v * sin (a) *t - (g * t * t) * 0.5; ///координаты по у для простого падения
49 Vy -= g * shag; ///значение скорости по у для метода эйлера
50 G[i] = G[i-1] + Vy * shag;///у из интегрирования по эйлеру
51 }
52 }
53
54 void SetVerle() ///функция для метода верле
55 {
56 double k = 0.1, m = 0.5; ///коэфф сопротивления водуха, масса тела
57 g = 9.8; /// коэфф свободного падения
58 uint32_t Size1 = 1000000.0; ///размер массива
59 S = new double [Size1]; ///создаем массив для значений по х для метода верле
60 Z = new double [Size1]; ///создаем массив для значений по у для метода верле
61 ///memset(S, 0, Size1 * sizeof(double));///обнуляем массив сначала
62 ///memset(Z, 0, Size1 * sizeof(double));///обнуляем массив сначала
63 vx = v * cos(a); ///формулы для вычисления скорости по оси х
64 vy = v * sin(a); ///формулы для вычисления скорости по оси у
65 S[1] = 0; ///значение х метод верле
66 S[0] = -vx * shag; ///значение в нуле
67 Z[1] = 0; ///значение у метод верле
68 Z[0] = -vy * shag; ///значение в нуле
69 for (int i = 0; i < Size1-2; i++) ///задаем цикл
70 {
71 S[i+2] = 2.0 * S[i+1] - S[i] - (k / m) * v * vx * shag * shag;///значения по х для верле
72 vx = 0.5 * ( 1.0 / shag )* ( S[i+2] - S[i]);///считаем значения скорости по оси х
73 Z[i+2] = 2.0 * Z[i+1] - Z[i] - ( g + (k / m) * v * vy ) * shag * shag;///значения по х для верле
74 vy = 0.5 * ( 1.0 / shag )* ( Z[i+2] - Z[i]);///считаем значения скорости по оси х
75 v = sqrt (vx * vx + vy * vy); ///модуль общей скорости
76 }
77 }
78 void SetVerleLast() ///функция для точного метода верле
79 {
80 double k = 0.1, m = 0.5;///коэфф сопротивления водуха, масса тела
81 g = 9.8; /// коэфф свободного падения
82 uint32_t Size2 = 1000000.0; ///размер массива
83 float t = 0; ///время
84 V = new double [Size2]; ///создаем массив для значений по х для точного метода верле
85 U = new double [Size2]; ///создаем массив для значений по у для точного метода верле
86 /// memset(U, 0, Size2 * sizeof(double));///копируем массив
87 ///memset(V, 0, Size2 * sizeof(double));///копируем массив
88 vx = v * cos(a); ///формулы для вычисления скорости по оси х
89 vy = v * sin(a); ///формулы для вычисления скорости по оси у
90 ///double e = 2.7 ;///значение экспоненты
91 V[0] = 0; ///значение х точный метод верле
92 U[0] = 0; ///значение у точный метод верле
93 for (int i = 1; i < Size2; i++)
94 {
95 t += shag; ///увеличиваем время на шаг
96 V[i] = vx * (m / k) * (1.0 - exp(((-k) / m) * t)); ///значения по х для точного верле
97 U[i] = (m / k) * (vy + g * (m / k)) * (1.0 - (exp(((-k) / m) * t))) - g * t * (m / k);///значения по х для точного верле
98 }
99 }
100
101 public: ///в открытом
102 pad()
103 {
104 X = 0; ///зануляем значения
105 Y = 0;
106 Size = 0;
107 v = 0;
108 shag = 0;
109 b = 0;
110 }
111 pad(double _v, double _shag, double _b) ///конструктор с параметрами
112 {
113 pi = M_PI; ///значение числа пи
114 g = 9.8; ///коэфф свободного падения
115 v = _v;/// присваиваем значения переменных значению параметров в конструкторе
116 shag = _shag;
117 b = _b;
118 a = (pi * b) / 180.0 ; ///вычисляем значение угла в радианах
119 double t = (2.0 * v * sin(a)) / g; /// считаем значение времени
120 Size = abs( t / shag )+1;///ищем значение размера массива
121 SetX(); ///вызываем функции зависящие от параметров конструктора
122 SetY();
123 SetVerle();
124 SetVerleLast();
125 }
126
127 void FilePrint() ///функция записи в файл
128 {
129 ofstream fout("output.txt"); ///открываем файл уже созданный в папке с программой
130 fout << "X: " << " Y: " << " E: " << " G: " << " S: " << " Z: "<< " V: "<< " U: "<<"\n" ; ///выводим стоку с разными названиями массивов, соотв. координатам по х и у различных методов
131 for (int i = 0; i < Size; i++) ///цикл
132 fout << X[i] << " " << Y[i] << " " << E[i] << " " << G[i] << " " << S[i] << " " << Z[i] << " " << V[i] <<" "<< U[i] <<"\n"; ///забивает сами значения массивов
133 fout.close();///закрываем файл
134 };
135 };
136
137 int main()/// основная функция
138 {
139 double shag, b, v; ///шаг, угол в градусах, скорость начальная
140 cout << "vvedite v "; ///просим пользователя ввести значение скорости начальной
141 cin >> v; ///считываем начальную скорость
142 cout << "vvedite ygol ";///просим пользователя ввести угол в градусах
143 cin >> b;/// считываем угол
144 cout << "vvedite shag ";///просим пользователя ввести шаг по времени
145 cin >> shag; ///считываем значение шага
146 pad F1(v, shag, b); ///объявление коструктора, создание функции F1 с переменными v, shag, b
147 F1.FilePrint(); ///вызываем функцию для записи файла
148 }
краткое описание алгоритма: в классе находятся координаты по формулам и записываются в файл.
инструкция : Пользователь должен ввести начальную скорость, угол и шаг, с которым будут рассчитываться координаты. В файл координаты записываются в таком порядке: 1, 2 столбики - Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; 3, 4 - Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; 5,6 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; 7,8 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости.
Скачать можно тут.
Иванова Яна
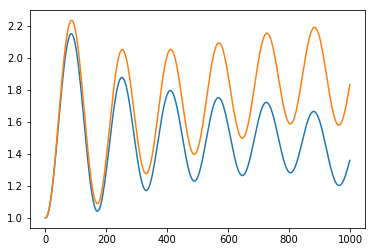
Описание программы: в программе выполняются четыре метода подсчета координат тела, брошенного под углом к горизонту. Координаты записываются в файл, строятся четыре графика, иллюстрирующие поведение тела при полете. Код написан для определенных начальных условий (для примера), если Вы хотите выполнить расчет для другой конфигурации, внесите изменения в начальные данные программы в самом коде.
Начальная скорость: 40 м/с, угол бросания: 45 градусов, коэффициент сопротивления воздуха: 0.023, шаг по времени : 0.1 секунды.
Скачать программу можно здесь
Визуализированный результат работы программы
File:graph.png
1 #include <iostream>
2 #include <math.h>
3 #include <iomanip>
4 #include <fstream>
5 #include <conio.h>
6
7
8 using namespace std;
9
10 ofstream outfile;
11
12 double perevod (double angle) //перевод из градусов в радианы
13 {
14 return (angle * M_PI / 180 );
15 }
16
17
18 int main()
19 {
20 //объявление переменных и задание начальных значений
21 double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V,
22 m = 1 , dt = 0.1 , g = 9.8,t = 0,
23 ugol = 45, alpha, R = 0.023, Xo = 0, Yo = 0, Vo = 40;
24
25 alpha = perevod (ugol);
26
27 //точное решение для случая движения без сопротивления воздуха
28 Y = Yo;
29 X = Xo;
30
31 outfile.open("1.txt");
32
33 while (Y >= Yo)
34 {
35 X = Xo + Vo * cos(alpha) * t;
36 Vx = Vo * cos(alpha);
37 Y = Yo + Vo * sin(alpha) * t - 0.5 * g * t * t;
38 Vy = Vo * sin(alpha) - g * t;
39 t += dt;
40
41 outfile << X << ' ' << Y << endl;
42 }
43 outfile.close();
44
45 //начальные условия для квадратичной зависимости (метод Верле)
46 Yprev = Yo - Vo*sin(alpha)*dt;
47 Xprev = Xo - Vo*cos(alpha)*dt;
48 X = Xo;
49 Y = Yo;
50 V = Vo;
51 Vx = Vo * cos(alpha);
52 Vy = Vo * sin(alpha);
53
54 outfile.open("2.txt");
55
56 while (Y >= Yo)
57 {
58 Xnext = 2.0 * X - Xprev - (R / m) * V * Vx * (dt * dt);
59 Vx = ( Xnext - Xprev )/ (2.0 * dt);
60 Ynext = 2.0 * Y - Yprev - (g + (R / m) * V * Vy) * (dt * dt);
61 Vy = (Ynext - Yprev)/ (2.0 * dt);
62 V = sqrt(Vy*Vy + Vx*Vx );
63 outfile << X << ' ' << Y << endl;
64
65 Xprev = X;
66 X = Xnext;
67 Yprev = Y;
68 Y = Ynext;
69 }
70 outfile.close();
71
72 //начальные условия для линейной зависимости (метод Верле)
73 Yprev = Yo - Vo*sin(alpha)*dt;
74 Xprev = Xo - Vo*cos(alpha)*dt;
75 X = Xo;
76 Y = Yo;
77 V = Vo;
78 Vx = Vo * cos(alpha);
79 Vy = Vo * sin(alpha);
80
81 outfile.open("3.txt");
82
83 while (Y >= Yo)
84 {
85 Xnext = 2.0 * X - Xprev - (R / m) * Vx * (dt * dt);
86 Vx = ( Xnext - Xprev )/ (2.0 * dt);
87 Ynext = 2.0 * Y - Yprev - (g + (R / m) * Vy) * (dt * dt);
88 Vy = (Ynext - Yprev)/ (2.0 * dt);
89 V = sqrt(Vy*Vy + Vx*Vx );
90 outfile << X << ' ' << Y << endl;
91
92 Xprev = X;
93 X = Xnext;
94 Yprev = Y;
95 Y = Ynext;
96 }
97 outfile.close();
98
99 //точное решения для линейной зависимости
100 Y = Yo;
101 X = Xo;
102 t = 0;
103
104 outfile.open("4.txt");
105
106 while (Y >= Yo)
107 {
108 Vx = Vo * cos(alpha);
109 Vy = Vo * sin(alpha);
110 X = (m * Vx / R)* (1 - exp(-1 * R * t / m));
111 Y = (m/R)*((Vy + g * m / R)*(1 - exp(-1 * R * t / m)) - g * t);
112 t += dt;
113 outfile << X << ' ' << Y << endl;
114 }
115 outfile.close();
116
117 return 0;
118
119 }
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
