Исследование деформирования горных пород

Руководители

Руководители со стороны СПбГПУ: В.А. Кузькин

Руководители со стороны ОАО "Газпромнефть НТЦ": С.В.Лукин

Материалы

1. Презентация
2. Диссертация

Аннотация

Данная работа затрагивает несколько тем связанных в гидроразрывом пласта (ГРП). Одной из них является раскрытие трещины под воздействием нагнетаемого флюида. Второй темой является связь статического и динамического модуля Юнга. В программном пакете Matlab создана математическая модель раскрытия трещины с ростом. Получены результаты характеризующие раскрытие трещины ГРП, влияние флюида на раскрытие трещины. В части механических свойств найдены корреляции связывающие статические и динамические модули Юнга для разных групп пористости пород-коллекторов.

Моделирование раскрытия трещины гидроразрыва пласта

Уравнение описывающие раскрытие трещины:

где w-раскрытие, [math]q_e[/math] - утечки в пласт, которые в данной задаче равны 0, [math]\mu[/math] - вязкость жидкости, [math]k=\frac{2E}{\pi h(1-\nu^2)}[/math], [math]E[/math] - модуль Юнга, [math]\nu[/math] - коэффициент Пуассона.

Граничные и начальные условия:

Математическая модель

Математическая модель реализована с помощью программного пакета Matlab с использованием конечно-разностей схемы Крана-Николсона. Решение системы алгебраических нелинейных уравнений производится в с помощью инерционного метода Ньютона. Начальное приближение задается соотвественно физическим представлениям о раскрытии трещины ГРП.

Исследование раскрытия растущей трещины гидроразрыва пласта

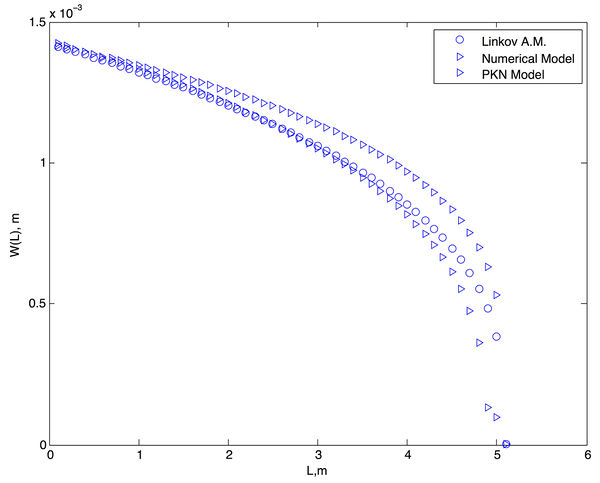
Результаты представлены ниже:

Графики сравнение между аналитическими решениями из работ [1,3] приводятся ниже.(W - раскрытие)

Влияние вязкости накачиваемой жидкости на раскрытие трещины гидроразрыва пласта

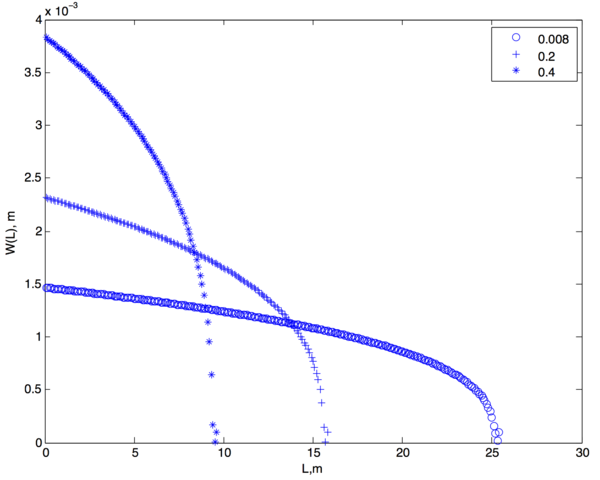
На основе проведенного исследования можно сделать вывод, что менее вязкий флюид обладает более проникающими способностями, что позволяет трещины расти в длину, в то время как менее вязкие жидкости позволяют трещине расти интенсивнее в ширину и высоту. На рисунке представлены графики раскрытия трещины для разных значений вязкости, от 0.008 до 0.4 [math]Pa \cdot c[/math]

Корреляции между статическим и динамическим модулем Юнга

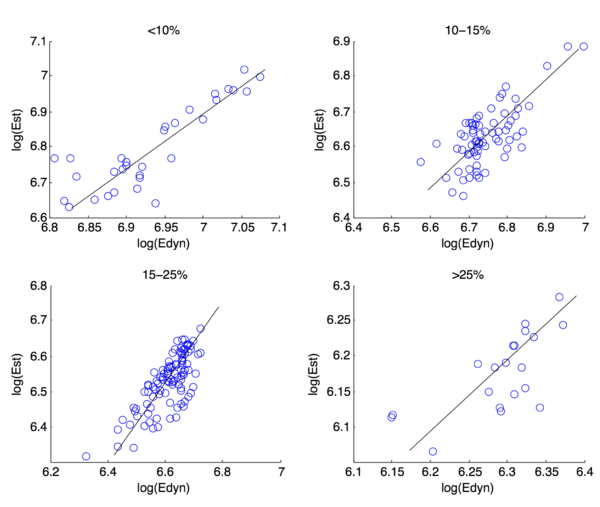
Для восстановления статического модуля Юнга при проектировании гидроразрыва пласта используют известные корреляции между статическим и динамическим модулем Юнга. В этой работе проанализировано более 200 лабораторных исследований керна полученных от ОАО "Газпромнефть". Данные разделены на 4 группы, в зависимости от пористости породы: <10%, 10-15%, 15-25%, >25% как это сделано в работе [2]. На рисунке изображены графике в логарифмической шкале. В таблице проводится сравнение между результатами работы [2] и результатами данной работы.

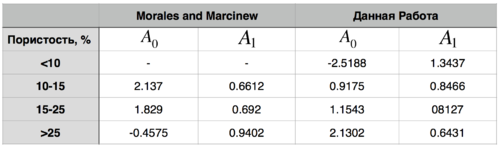
Результаты исследования Morales and Marcinew в 1993 году представлены здесь в разделе CALIBRATING DYNAMIC TO STATIC CONSTANTS, а также на сайте OnePetro оригинал статьи.

Ниже представлена таблица для коэффициентов уравнения:

Результаты

1. Решены тестовые задачи на основе явной и неявной численной схемы Эйлера

2. Реализована конечно-разностная схема решения уравнения раскрытия трещины в пакете Matlab

3. Проверена на сходимость численной схемы

4. Проанализировано влияние вязкости на раскрытие и длину трещины

5. Произведено сравнение с аналитическим решением

6. Определены корреляции статического и динамического модуля Юнга