Свободные колебания платформы в вертикальной плоскости

Виртуальная лаборатория>Свободные колебания платформы в вертикальной плоскости

---

Что собой представляет система
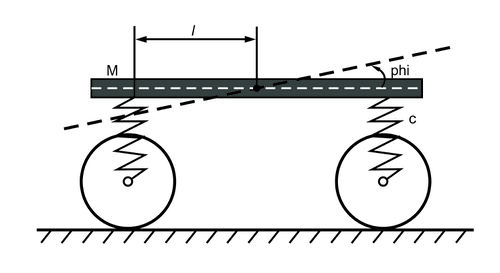
Платформа, закрепленная на пружинах, совершает колебания в вертикальной плоскости.

Постановка задачи
Исследовать свободные колебания платформы массы [math]{M}[/math], если расстояние центра тяжести платформы от вертикальных плоскостей, проведенных через оси колесных пар, [math]l_{1} = l_{2} = l[/math]. Радиус инерции относительно центральной поперечной оси вагона [math]i_{Cy}[/math], жесткость рессор для всех осей одинакова и равна [math]С[/math]. Массой рессор и силами трения пренебрегаем.

Основные уравнения

[math] a_{1}=\frac{G}{g}\\ a_{2}=\frac{G}{g}i_{Cy}^{2}\\ с_{1}=4c\\ c_{2}=4cl^{2}\\ [/math]

Частоты главных колебаний

[math] k_{1}=\sqrt{\frac{c_{1}}{a_{1}}}=\sqrt{\frac{4cg}{G}}\\ k_{2}=\sqrt{\frac{c_{2}}{a_{2}}}=\sqrt{\frac{4cl^{2}g}{Gi_{Cy}^{2}}} [/math]

Уравнения движения системы в главных координатах

[math] z=C_{1}sin(k_{1}t+\alpha_{1})\\ phi=C_{2}sin(k_{2}t+\alpha_{2}) [/math]