КП: Прицельный бильярд
Курсовой проект по Теоретической механике
Исполнитель: Степанов Матвей
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Аннотация проекта
Проект направлен на изучение динамики взаимодействия шаров при игре в бильярд. В ходе работы над проектом рассмотрен удар под названием "резка", написана программа, на языке JavaScript, моделирующая игровой процесс.
Формулировка задачи
- Написать программу, моделирующую динамику взаимодействия шаров при игре в Бильярд. Взаимодействие между шарами описывается с помощью потенциала Леннарда-Джонса.
- Реализовать сложные комбинации при игре в Бильярд.
Общие сведения по теме
Характерной особенностью всех бильярдных игр является передвижение шаров с помощью кия. Основные характерные особенности: шары, незначительно уступающие по размерам створу лузы (диаметр шара 68-68,5 мм., а вес около 285 г.) ширина створа угловой лузы 72-73 мм, средней лузы 82-83 мм).
При реализации данной задачи используется стол с размерами игрового поля 2240 х 1120 мм, диаметром шара 68 мм и размерами луз 72 и 82 мм соответственно.
Программа для игры в Бильярд
Ниже приведена программа( созданная совместно с Булдаковым Павлом на основании программы Динамика взаимодействующих частиц), в которой видно, что траектория разлета шаров схожа с расчетными траекториями полученными профессором Джимом Белк (рис.1). Взаимодействие между шарами описывается с помощью потенциала Леннарда-Джонса.
где
— расстояние между частицами,
— энергия связи,
— длина связи.
Файл "Billyard1version.js"
1 window.addEventListener("load", MainBalls, true);
2 function MainBalls(slider_01, text_01, slider_02, text_02) {
3
4 // Предварительные установки
5
6 var canvas = canvasBalls;
7 var context = canvas.getContext("2d"); // на context происходит рисование
8 canvas.oncontextmenu = function (e) {return false;}; // блокировка контекстного меню
9
10 var Pi = 3.1415926; // число "пи"
11
12 var m0 = 1; // масштаб массы
13 var T0 = 1; // масштаб времени (период колебаний исходной системы)
14 var a0 = 1; // масштаб расстояния (диаметр шара)
15 var q = -90; // угол
16
17
18 var g0 = a0 / T0 / T0; // масштаб ускорения (ускорение, при котором за T0 будет пройдено расстояние a0)
19 var k0 = 2 * Pi / T0; // масштаб частоты
20 var C0 = m0 * k0 * k0; // масштаб жесткости
21 var B0 = 2 * m0 * k0; // масштаб вязкости
22 var v0 = 1; //начальная скорость
23
24
25 // *** Задание физических параметров ***
26
27 var Ny = 32; // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
28 var m = 1 * m0; // масса
29 var Cwall = 10 * C0; // жесткость стен
30 var Cball = 0.1 * Cwall; // жесткость между частицами
31 var B = 0.008 * B0; // вязкость среды
32 var Bwall = 0.03 * B0; // вязкость на стенках
33 var mg = 0.25 * m * g0; // сила тяжести
34 var r = 0.5 * a0; // радиус частицы в расчетных координатах
35 var K = 0.85; // сила взаимодействия ограничивается значением, реализующимся при r/a = K
36 var a = 2 * r; // равновесное расстояние между частицами
37 var aCut = 2.00001 * r; // радиус обрезания
38
39 // *** Задание вычислительных параметров ***
40
41 var fps = 50; // frames per second - число кадров в секунду (качечтво отображения)
42 var spf = 100; // steps per frame - число шагов интегрирования между кадрами (скорость расчета)
43 var dt = 0.045 * T0 / fps; // шаг интегрирования (качество расчета)
44
45 // Выполнение программы
46
47 var scale = canvas.height / Ny / a0; // масштабный коэффициент для перехода от расчетных к экранным координатам
48 var r2 = r * r; // ___в целях оптимизации___
49 var aCut2 = aCut * aCut; // ___в целях оптимизации___
50 var a2 = a * a; // ___в целях оптимизации___
51 var D = a2 * Cball / 72; // энергия связи между частицами
52 var LJCoeff = 12 * D / a2; // коэффициент для расчета потенциала Л-Дж
53
54 var Ka = K * a; // ___в целях оптимизации___
55 var K2a2 = K * K * a2; // ___в целях оптимизации___
56
57 var w = canvas.width / scale; // ширина окна в расчетных координатах
58 var h = canvas.height / scale; // высота окна в расчетных координатах
59
60 // Работа с массивом
61
62 var balls = []; // массив шаров
63 var addNewBall = function(x, y) {
64 // проверка - не пересекается ли новый шар со стенами или уже существующими шарами
65 if (x - r < 0 || x + r > w || y - r < 0 || y + r > h) return null;
66 for (var i = 0; i < balls.length; i++) {
67 var rx = balls[i].x - x;
68 var ry = balls[i].y - y;
69 var rLen2 = rx * rx + ry * ry;
70 if (rLen2 < 4 * r2) return null;
71 }
72 var b = [];
73
74 b.x = x; b.y = y; // расчетные координаты шара
75 b.fx = 0; b.fy = 0; // сила, действующая на шар
76 b.vx = 0; b.vy = 0; // скорость
77
78 balls[balls.length] = b; // добавить элемент в конец массива
79 return b;
80 };
81
82 // Основной цикл программы
83
84 function control() {
85 physics();
86 draw();
87 }
88
89 // Расчетная часть программы
90
91 function physics() { // то, что происходит каждый шаг времени
92 for (var s = 1; s <= spf; s++) {
93
94 // пересчет сил идет отдельным массивом, т.к. далее будут добавляться силы взаимодействия между шарами
95 for (var i0 = 0; i0 < balls.length; i0++) {
96 balls[i0].fx = - B * balls[i0].vx;
97 balls[i0].fy = - B * balls[i0].vy;
98 }
99
100 for (var i = 0; i < balls.length; i++) {
101
102
103 //попадание в лузу
104
105 if ((balls[i].x >= (300/scale-r)) && (balls[i].y >= (300/scale-r)) && (balls[i].y <= (300/scale+r))) {balls.splice(i, 1)};
106 if ((balls[i].x >= (300/scale-r)) && (balls[i].y <= (r))) {balls.splice(i, 1)};
107 if ((balls[i].x >= (300/scale-r)) && (balls[i].y >= (600/scale -r))) {balls.splice(i, 1)};
108 if ((balls[i].x <= (r)) && (balls[i].y >= (600/scale -r))) {balls.splice(i, 1)};
109 if ((balls[i].x <= (r)) && (balls[i].y >= (300/scale-r)) && (balls[i].y <= (300/scale+r))) {balls.splice(i, 1)};
110 if ((balls[i].x <= (r)) && (balls[i].y <= (r))) {balls.splice(i, 1)};
111
112 // расчет взаимодействия производится со всеми следующими шарами в массиве,
113 // чтобы не считать каждое взаимодействие дважды
114 var b = balls[i];
115 for (var j = i + 1; j < balls.length; j++) {
116 var b2 = balls[j];
117 var rx = b.x - b2.x; var ry = b.y - b2.y; // вектор смотрит на первый шар (b)
118 var r2 = rx * rx + ry * ry; // квадрат расстояния между шарами
119 if (r2 > aCut2) continue; // проверка на радиус обрезания
120 var rLen = (Math.sqrt(r2));
121
122
123 // если расстояние между частицами мало, силы будут посчитаны для K * a
124 if (r2 < K2a2) {
125 if (rLen > 0.00001) { // проверка, чтобы избежать деления на 0
126 rx = rx / rLen * Ka;
127 ry = ry / rLen * Ka;
128 }
129 r2 = K2a2;
130 rLen = Ka; // корень K2a2
131 }
132
133 // сила взаимодействия
134 var s2 = a2 / r2; var s4 = s2 * s2; // ___в целях оптимизации___
135 var F = LJCoeff * s4 * s4 * (s4 * s2 - 1); // сила взаимодействия Леннарда-Джонса
136
137 var Fx = F * rx; var Fy = F * ry;
138 b.fx += Fx; b.fy += Fy;
139 b2.fx -= Fx; b2.fy -= Fy;
140 }
141
142 if (b.y + r > h) { b.fy += -Cwall * (b.y + r - h) - Bwall * b.vy; }
143 if (b.y - r < 0) { b.fy += -Cwall * (b.y - r) - Bwall * b.vy;}
144 if (b.x + r > w) { b.fx += -Cwall * (b.x + r - w) - Bwall * b.vx; }
145 if (b.x - r < 0) { b.fx += -Cwall * (b.x - r) - Bwall * b.vx; }
146
147 b.vx += b.fx / m * dt; b.vy += b.fy / m * dt;
148 b.x += b.vx * dt; b.y += b.vy * dt;
149 }
150 }
151 }
152
153 // Рисование
154
155 var rScale13 = r * scale * 1.3; // ___в целях оптимизации___
156 var rScaleShift = r * scale / 5; // ___в целях оптимизации___
157 var line ;
158 var radi = 30;
159 var radi2 = 5;
160
161 function draw() {
162 context.clearRect(0, 0, w * scale, h * scale); // очистить экран
163 for (var i = 0; i < balls.length; i++){
164 var xS = balls[i].x * scale; var yS = balls[i].y * scale;
165 // расчет градиента нужно проводить для каждого шара
166 var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
167 gradient.addColorStop(0, "#fdebeb");
168 gradient.addColorStop(1, "#fffcfc");
169 context.fillStyle = gradient;
170
171 context.beginPath();
172 context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
173 context.closePath();
174 context.fill();
175 }
176 for (var i = 15; i < balls.length; i++){
177 var xS = balls[i].x * scale; var yS = balls[i].y * scale;
178 // расчет градиента нужно проводить для каждого шара
179 var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
180 gradient.addColorStop(0, "#cd0000");
181 gradient.addColorStop(1, "#fffcfc");
182 context.fillStyle = gradient;
183
184 context.beginPath();
185 context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
186 context.closePath();
187 context.fill();
188 }
189
190
191
192 context.lineWidth="3";
193 context.strokeStyle="#fff506";
194 context.beginPath();
195 context.moveTo(balls[15].x * scale, balls[15].y * scale);
196 context.lineTo(radi*v0*Math.cos(q*Pi/180) + balls[15].x * scale,radi*v0*Math.sin(q*Pi/180)+balls[15].y * scale);
197 context.stroke();
198
199
200 // verh lev
201 context.lineWidth="3";
202 context.strokeStyle="#ffffff ";
203 context.beginPath();
204 context.moveTo(0, 0);
205 context.lineTo(0,14 +2.5 );
206 context.stroke();
207
208 context.lineWidth="3";
209 context.strokeStyle="#ffffff";
210 context.beginPath();
211 context.moveTo(0, 0);
212 context.lineTo(14 +2.5,0 );
213 context.stroke();
214
215 // verh prav
216 context.lineWidth="3";
217 context.strokeStyle="#ffffff";
218 context.beginPath();
219 context.moveTo(286 - 2.5, 0);
220 context.lineTo(300,0 );
221 context.stroke();
222
223 context.lineWidth="3";
224 context.strokeStyle="##ffffff";
225 context.beginPath();
226 context.moveTo(300, 0);
227 context.lineTo(300,14 +2.5 );
228 context.stroke();
229
230 // niz lev
231 context.lineWidth="3";
232 context.strokeStyle="#ffffff";
233 context.beginPath();
234 context.moveTo(0, 600);
235 context.lineTo(14 +2.5,600 );
236 context.stroke();
237
238 context.lineWidth="3";
239 context.strokeStyle="#ffffff";
240 context.beginPath();
241 context.moveTo(0, 586 - 2.5);
242 context.lineTo(0,600 );
243 context.stroke();
244
245
246 // niz prav
247 context.lineWidth="3";
248 context.strokeStyle="#ffffff";
249 context.beginPath();
250 context.moveTo(300, 600);
251 context.lineTo(300,586 - 2.5);
252 context.stroke();
253
254 context.lineWidth="3";
255 context.strokeStyle="#ffffff";
256 context.beginPath();
257 context.moveTo(300, 600);
258 context.lineTo(286 - 2.5,600 );
259 context.stroke();
260
261 //sered lev
262 context.lineWidth="3";
263 context.strokeStyle="#ffffff";
264 context.beginPath();
265 context.moveTo(0, 289);
266 context.lineTo(0,311);
267 context.stroke();
268
269 //sered prav
270
271 context.lineWidth="3";
272 context.strokeStyle="#ffffff";
273 context.beginPath();
274 context.moveTo(300, 289);
275 context.lineTo(300,311 );
276 context.stroke();
277
278
279 }
280
281
282 // Запуск системы
283 addNewBall(16*w/32, 8*h/32 );
284 addNewBall(16*w/32 - r, 8*h/32 - 1.7321*r);
285 addNewBall(16*w/32 + r, 8*h/32 - 1.7321*r );
286 addNewBall(16*w/32, 8*h/32 - 2*1.7321*r );
287 addNewBall(16*w/32 - 2*r, 8*h/32 - 2*1.7321*r );
288 addNewBall(16*w/32 + 2*r, 8*h/32 - 2*1.7321*r );
289 addNewBall(16*w/32 + r, 8*h/32 - 3*1.7321*r );
290 addNewBall(16*w/32 - r, 8*h/32 - 3*1.7321*r );
291 addNewBall(16*w/32 + 3*r, 8*h/32 - 3*1.7321*r );
292 addNewBall(16*w/32 - 3*r, 8*h/32 - 3*1.7321*r );
293 addNewBall(16*w/32, 8*h/32 - 4*1.7321*r );
294 addNewBall(16*w/32 - 2*r, 8*h/32 - 4*1.7321*r );
295 addNewBall(16*w/32 + 2*r, 8*h/32 - 4*1.7321*r );
296 addNewBall(16*w/32 - 4*r, 8*h/32 - 4*1.7321*r );
297 addNewBall(16*w/32 + 4*r, 8*h/32 - 4*1.7321*r );
298 addNewBall(16*w/32, 16*h/32 );
299
300 this.setSlider_01 = function(c) { q=c ;}; // функция для слайдера угла
301 this.setSlider_02 = function(c) { v0=c ;}; // функция для слайдера угла
302
303 // Настройка интерфейса
304
305 slider_01.min = -360; slider_01.max =180;
306 slider_01.step = 0.1;
307 slider_01.value = q; // начальное значение ползунка должно задаваться после min и max
308 text_01.value = -q;
309 slider_02.min = 0; slider_02.max = 10;
310 slider_02.step = 0.5;
311 slider_02.value = v0; // начальное значение ползунка должно задаваться после min и max
312 text_02.value = v0;
313
314 this.setSlider_01(q);
315 this.setSlider_02(v0);
316
317 this.newSystem = function() {
318 balls[15].vx = v0* Math.cos(q*Pi/180);
319 balls[15].vy = v0* Math.sin(q*Pi/180);
320 }
321
322 setInterval(control, 1000 / fps);
323 }
Файл "Billyard1version.html"
1 <!DOCTYPE html>
2 <html>
3 <head>
4 <title>Billyard</title>
5 <script src="Billyard1version.js"></script>
6 </head>
7 <body>
8 <canvas id="canvasBalls" width="300" height="600" style="border:1px none #000000;background: #008000"></canvas>
9 <br>
10 <div>Угол:
11 <input type="range" id="slider_01" style="width: 150px;" oninput="app.setSlider_01(this.value); document.getElementById('text_01').value = this.value;">
12 q =
13 <input id="text_01" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
14 // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
15 if (!this.checkValidity()) return;
16 app.setSlider_01(this.value);
17 document.getElementById('slider_01').value = this.value;
18 ">
19 </div><br>
20
21 <div>Начальная скорость:
22 <input type="range" id="slider_02" style="width: 150px;" oninput="app.setSlider_02(this.value); document.getElementById('text_02').value = this.value;">
23 v0 =
24 <input id="text_02" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
25 // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
26 if (!this.checkValidity()) return;
27 app.setSlider_02(this.value);
28 document.getElementById('slider_02').value = this.value;
29 ">
30 </div><br>
31
32
33 <input type="button" style="width: 50px" name="" onclick="app.newSystem();return false;" value="PLAY"/>
34
35
36 <script type="text/javascript">var app = new MainBalls(
37 document.getElementById('slider_01'),
38 document.getElementById('text_01'),
39 document.getElementById('slider_02'),
40 document.getElementById('text_02')
41 );</script>
42 </body>
43 </html>
Решение
Задача: Рассчитать скорость и угол направления удара, а так же возможные расположения шаров, при которых оба шара (рис.2) окажутся в верхних лузах.
На рис.2, один из шаров(биток) смещен с оси прямого удара, таким образом появляется резка. Нужно попасть битком в точку на прицельном шаре, от которой через математический центр прицельного шара до центра лузы проходит прямая линия. При малой резке эта точка на прицельном шаре еще видна, но по мере увеличения резки она становится практически невидимой.
Правило 90°: когда "биток" ударяет прицельный шар, скользя по сукну без переднего или заднего вращения, шары разлетаются под углом 90° друг к другу. Правило работает независимо от угла резки.
- скорость "битка" до и после соударения.- скорость прицельного шара после соударения.
Из ЗСИ:
(1)
Из ЗСЭ:
(2)
Скалярное произведине ур-ния (1) самого на себя дает:
(3)
(3) - (2):
, а это возможно, если (что соответствует прямому удару), или при
Примечание :Вывод правила 90° основан на двух существенных допущениях: трение между шарами равно нулю и столкновение шаров – абсолютно упругое.
Будем считать, что шары однородные и совершенно сферической формы.
- углы отклонения первого и второго шаров после столкновения по отношению к направлению удара. - угол поворота первого шара в системе центра инерции.
- абсолютные величины скоростей шаров после столкновения.
, где
Рассмотрим частный случай (рис.2):
мм. - расстояние от прицельного шара до верхней левой лузы, мм. - расстояние от битка до верхней правой лузы, в момент соприкосновения шаров, мм. - расстояние между шарами в начальный момент времени.
Угол разлета шаров после удара 90°, значит можем рассчитать
В таком случае, после соударения шаров, они приобретут скорости:
, где искомая скорость , т.к. в нашем случае прицельный шар в начальный момент времени неподвижен.
В рассмотренном случае угол, под которым производится удар, по отношению к оси OX равен . В общем случае этот угол зависит от расположения битка.
Обсуждение результатов и выводы
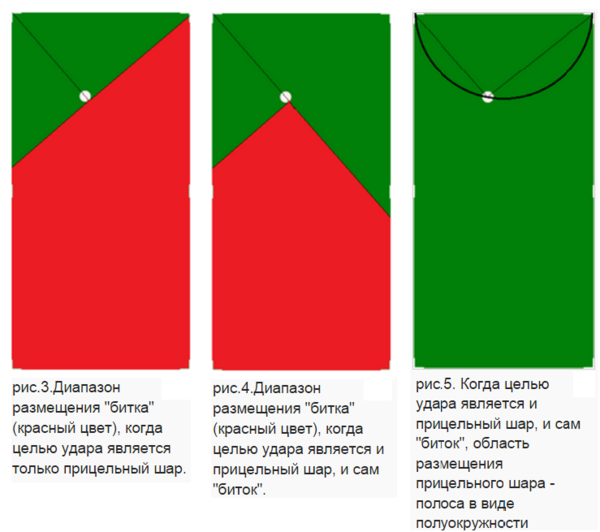
Таким образом, в ходе работы над проектом была написана программа, моделирующая процесс игры в бильярд, а так же смоделирован рассматриваемый удар, целью, которого являются оба шара. Были рассчитаны скорость и угол направления удара в рассматриваемом случае. Установлены возможные положения шаров, когда целью удара является один или оба шара (рис.3 и рис.4). А на рис.5 указана область расположения для прицельного шара, когда стоит задача загнать в верхние лузы оба шара.
Скачать отчет:
Скачать презентацию: