КП: Многочастичный симулятор

А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Многочастичный симулятор

---

Ткань из пружин

Курсовой проект по Теоретической механике

Исполнитель: Старобинский Егор

Группа: 09 (23604)

Семестр: весна 2015

Формулировка задачи

Цель работы

Создание интернет-сайта, позволяющего пользователю моделировать многоточечную систему онлайн.

Решаемые задачи

1. решение уравнения движения;
2. визуализация.

Общие сведения по теме

Уравнение движения

Пусть мы наблюдаем тело в момент времени [math]t[/math].

Хотим знать, где окажется тело через малое изменение времени - [math]\Delta t[/math]. Рассмотрим базовый метод Верле :

[math]\vec{x}(t + \Delta t) = 2\vec{x}(t) - \vec{x}(t - \Delta t) + \vec{R}(t) \Delta t^2 / m[/math], где

[math]\vec{x}[/math] - позиция точки,

[math]\vec{R}[/math] - равнодействующая всех сил, действующих на тело,

[math]m[/math] - масса тела,

[math]t[/math] - текущий момент времени,

[math]\Delta t[/math] - малое изменение времени.

Метод Верле позволяет вычислять траекторию по упрощённой схеме: зная предыдущее и текущее положения ([math]\vec{x}(t - \Delta t)[/math] и [math]\vec{x}(t)[/math] соответственно)  и мгновенное значение равнодействующей приложенных сил в текущем положении [math]\vec{R}(t)[/math].

Язык реализации: JavaScript.

Визуализация

Язык рализации: pure SCSS. Обработка событий: JavaScript.

Решение

Нахождение периода в простом движении

Элементы системы

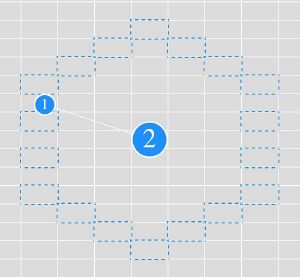
• Частицы;
• Стержни и пружины;
• Стенки;
• Поле сил;
• Рабочее окно;
• Консоль;
• Плеер.

Пример вывода консоли

Возможности консоли

• Конфигурация начальной системы тел;
• Изменение системы в процессе работы ("на лету");
• Запуск алгоритмов анализа системы;
• Распознавание и вывод ошибок в пользовательских запросах и в исходном коде;
• Распознавани и вывод предупреждений в пользовательских запросах и в исходном коде;
• Тетрис.

Возможности плеера

• Воспроизведение/пауза симуляции с заданным [math]\Delta t[/math];
• Скачок вперёд на кратное [math]\Delta t[/math] время;
• "Замедление времени".

Обсуждение результатов и выводы

Скачать отчет:
Скачать презентацию:

Ссылки по теме

Опорный материал: Thomas Jakobsen. "Advanced Character Physics", January 21, 2003. (перевод статьи [pdf])

См. также

• Справочная информация
• Курсовые проекты ТМ