Statistical mechanics of glass

Introduction

The field of glass science is quickly maturing from a purely empirical science to one built upon rigorous fundamental physics. These advancements offer an unprecedented level of understanding of the glass transition and the glassy state, as well as the ability to design new glass compositions starting at the atomic level. As a nonequilibrium material, the structure and properties of glass depend not only on its composition, but also on its thermal and pressure histories. Since glass is thermodynamically unstable, it is continually relaxing toward the metastable supercooled liquid state. Owing to this time dependence of glass properties and microstructure, traditional reversible thermodynamics cannot be directly applied to study the glassy state. While some nonequilibrium aspects of the glassy state can be estimated using irreversible thermodynamics, this approach has no microscopic basis and hence cannot offer a rigorous physical description of either the glass transition or glass itself. Alternatively, nonequilibrium statistical mechanics offers a framework in which the macroscopic properties of a glass can be rigorously calculated from its microscopic structure. As such, statistical mechanics has many practical applications in glass science and technology. The objective of this article is to provide an overview of various statistical mechanical descriptions of the glassy state and their practical use in understanding glass physics and in the design of new glass compositions. The relationship among these various descriptions is emphasized to build a single unified picture of glass statistical mechanics synthesizing these various approaches.

Glass and the glass transition

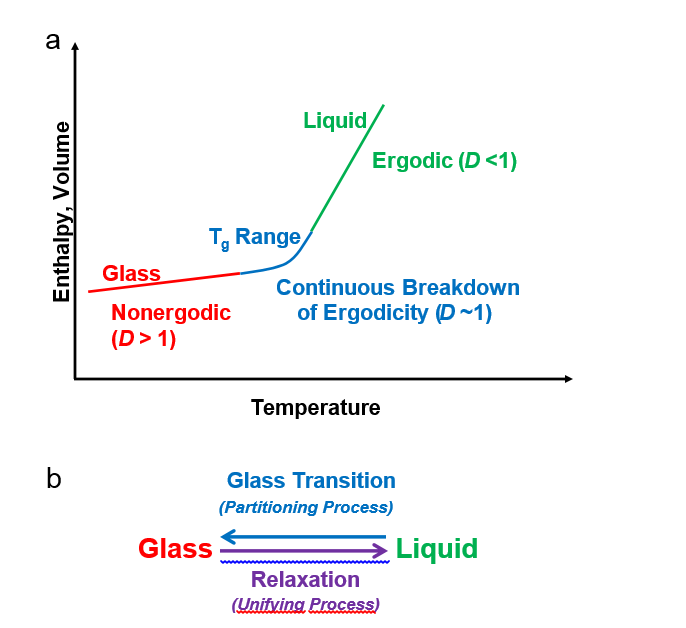
Glass and the glass transition are widely considered as two of the most challenging problems in condensed matter physics. Glass is challenging at a microscopic level due to its non-crystalline structure, lacking the long-range order characteristic of crystalline solids. At a thermodynamic level, glass is difficult since it is a nonequilibrium material. As such, the properties of a glass are not a simple function of composition, temperature, and pressure: the entire thermal history (and pressure history, if applicable) of a glass must be considered. Furthermore, the properties of a glass evolve as it continually relaxes toward its corresponding metastable equilibrium liquid state. One of the main challenges of glass science is to capture this complicated composition and time dependence of glass properties in a manner that is physically rigorous and quantitatively accurate. While the thermodynamics of equilibrium materials is well understood the same cannot be said for nonequilibrium systems such as glass. The field of irreversible thermodynamics seeks to overcome these limitations by introducing one or more additional parameters, called “order parameters,” responsible for describing the nonequilibrium state of the glass. However, irreversible thermodynamics is phenomenological by design and hence is not rooted in any fundamental physics. Moreover, there is no direct connection to the underlying microscopic physics of the system, e.g., the notion of atomic structure plays no role in either reversible or irreversible thermodynamics.

Statistical mechanics

The connection between microscopic and macroscopic physics is provided by statistical mechanics. Many processes that occur on the atomic level are stochastic in nature, such as thermal fluctuations and transitions between microstates. While in classical mechanics these processes may be considered deterministic, our lack of detailed knowledge of the exact dynamics of each atom in the system requires the use of a statistical approach. Statistical mechanics addresses this issue by using probability theory to determine expectation values for macroscopic properties averaged over a suitable ensemble of microstates. However, the application of statistical mechanics to the glassy state is not necessarily straightforward, since most statistical mechanical approaches make an implicit assumption of ergodicity, i.e., the equivalence of time and ensemble averages of the properties of interest. Glass is nonergodic by its very nature and hence requires special care in developing rigorous statistical theory. For glass scientists, the development of new statistical mechanical models is especially exciting.

Ergodic theory

In statistical theory, the term ergodic refers to an equivalence of the time and ensemble averages of the properties of a system. Ergodicity is a common assumption in equilibrium statistical mechanics. However, for nonequilibrium systems such as glass, the ensemble average of certain thermodynamic properties can be different from the corresponding time average. For example, an ensemble average includes frozen-in fluctuations that may not be present in a time average of the same property. For any experiment, the question of ergodicity is really a question of time scale. Specifically, there are two relevant time scales of interest: an internal relaxation time scale (τint) on which the system loses memory of its preceding states, and an external observation time scale (τext) on which properties are measured. Reiner defined the ratio of these two time scales as the “Deborah number” of the experiment.

Scientific point of view

From a purely scientific point of view, the insights from statistical mechanics are key to resolving the apparent contradictions of glass with the second and third laws of thermodynamics, confirming that a nonequilibrium glass must obey these laws just as every other material. More importantly, these statistical mechanical techniques offer a rigorous approach for modeling the impact of glass composition and thermal history on its structure and properties. Given the rigorous nature of the approach, the models are quantitatively predictive without the need for empirical fitting parameters. Clearly the field of glass science has advanced dramatically since the days when all new discoveries were made through trial-and-error experimentation. However, as discussed earlier, there are still many unsolved problems in glass physics, many of which may be addressed through statistical mechanical techniques . Considering these new opportunities for innovation, there has certainly never been a more exciting time to be a researcher in the science of glass.