Оптимизация подбора вакуумных присосок для промышленных роботов

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Р.Н.Симонов
Руководитель: Ле-Захаров А.А.

Введение

Вакуумная присоска - это элементы, предназначенные для захвата и перемещения изделий и заготовок с помощью вакуума. Как правило, вакуумные присоски очень часто используются в промышленном производстве для подъема предметов, имеющих гладкие воздухонепроницаемые поверхности,но возможен так же захват некоторых пористых и выпуклых поверхностей,применяются преимущественно при работе с листовыми деталями.
Эти захваты отличает простота конструкции и небольшая масса. Наиболее распространенная конструкция вакуумного захвата. Одним из основных элементов этих схватов является чашка-присоска, которая делается обычно из резины или пластмассы. Присоски используются также для захвата стеклянных деталей со сложной наружной поверхностью или для захвата нескольких разных по форме, но близких по размеру деталей. Иногда присоски делаются в виде пластин с большим количеством отверстий, каждое из которых предназначено для захвата одной детали.
Откачивание воздуха из-под присоски производится вакуумным насосом через шланг, протянутый вдоль руки робота, или с помощью эжектора, работающего от цеховой сети сжатого воздуха.
Основные области применения вакуумных присосок - это автоматизация различных производств: деревообрабатывающего, пищевого, автомобильного, стекольного.
Характеристика вакуумных захватов:
Сила притяжения на единицу площади ограничена. Снижена точность базирования через эластичность конструкции. Необходимо некоторое время для создания вакуума. Срок службы ограниченный;

Тонкая пластина — пластинкой называют тело, ограниченное двумя плоскостями, расстояние между которыми мало по сравнению с размерами этих плоскостей (толщина пластинки). Плоскость, равноудаленная от поверхностей пластины, называется срединной плоскостью. Линия пересечения срединной плоскости с ограничивающими пластинку боковыми поверхностями образует контур пластинки. Поперечные нагрузки, т.е. силы, перпендикулярные к срединной плоскости, а так же моменты вызывают ее изгиб. Такие пластины широко распространены в технике (крышки резервуаров, плоские участки обшивки крыла самолета и т.д.).

Гипотезы Кирхгоффа теории изгиба пластин:
Гипотезы являются обобщением гипотез Бернулли, которые используются при расчете изгиба балок. В этих гипотезах принимается, что поперечные сечения балки остаются плоскими и нормальными к ее оси в процессе изгиба и волокна балки не надавливают друг на друга. Для пластинок гипотезы формулируются так:
1.Нормаль к срединной поверхности не искривляется, а только поворачивается при изгибе пластинки. Это означает, что сдвиги в плоскостях, проходящих через нормаль к срединной поверхности, равны нулю.
2.Нормаль к срединной поверхности не растягивается.
3.Нормальными напряжениями на площадках, параллельных срединной плоскости, можно пренебречь по сравнению с другими напряжениями.
4.Срединная поверхность не растягивается и не сжимается, т.е. нормальные напряжения на ней равны нулю.

Постановка Задачи

В ходе различных экспериментов найти оптимальный набор вакуумных присосок для захвата объекта с минимально допустимым прогибом. Для достижения поставленной цели решаются задачи:

1) создание наиболее простой компьютерной 3D модели вакуумной чашки и пластины.
2) создание конечно-элементной модели пластины.
3) нахождение наилучшего соотношения расположения и количества вакуумных присосок для объекта прямоугольного профиля.
4) исследование прогиба пластины прямоугольного профиля при вертикальном перемещении.

Компьютерная 3D модель

Первая часть работы заключалась в построении простой компьютерной 3D модели тонкой пластины прямоугольного профиля и вакуумной присоски в программе инженерного моделирования Solid Works.
Построение данной модели наглядно показывает разновидности компоновки вакуумных присосок относительно прямоугольной тонкой пластины, которые в дальнейшем будут использованы для расчета перемещений (прогиба) прямоугольной пластины.
В работе было рассмотрено 5 частных случаев компоновки:
1.Вакуумная чашка располагается в центре пластины: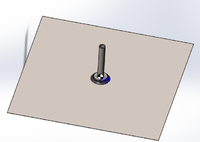

2.Вакуумные чашки располагаются в форме квадрата: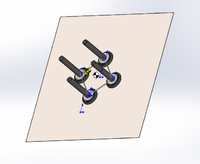

3.Вакуумные чашки располагаются в форме креста:

4.Вакуумные чашки располагаются в форме правильного шестиугольника: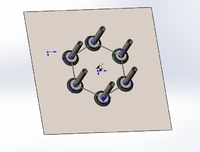

5.Вакуумные чашки располагаются в 3 ряда и 3 столбца:

Конечно-элементная модель

Расчеты изгиба пластины проводились методом конечных элементов (МКЭ) в программе инженерного моделирования ABAQUS.
Для расчета был выбран оболочный тип построения Shell.
Материал профиля пластины – сталь с характеристиками: E =205 ГПа, ν =0.29, в упругой постановке.

Исследуемый объект прямоугольный профиль с толщиной 0.5мм. Длина – 400мм, ширина – 400мм. В данной постановке задач не рассматривается прогиб пластины в области приложения вакуумной чашки.
Граничные условия:

• Область под вакуумной чашкой: круг – жесткая заделка.
  
• Свободные края тонкой прямоугольной пластины.
  

Модель подвержена нагружению:

• Равномерно распределенное давление P = 7.7 Па
  

В результате данного этапа необходимо найти:

• Перемещения (прогиб) пластины для 5 частных случаев.(максимальный прогиб должен не превышать 1мм).
  

Результаты

1.Вакуумная чашка расположена в центре пластины:
2.Вакуумные чашки расположены в форме квадрата:
3.Вакуумные чашки расположены в форме правильного шестиугольника:
4.Вакуумные чашки расположены в 3 ряда и 3 столбца:
5.Вакуумные чашки расположены в форме креста:

Анализ расчетов
1.В результате проведенных расчетов выявилось, что вариант закрепления вакуумной чашки в середине пластины (№1) очень близок к критическому прогибу 1мм, что не удовлетворяет поставленной задаче.
2.Наилучшие показатели были выявлены в варианте №4, где вакуумные чашки были расположены в 3 ряда и 3 столбца. Такой результат был достигнут за счет большого кол-ва заделок.
Был построен график сходимости перемещений (прогибов) от кол-ва разбиений в профиле для варианта №4, для показания точности проведенных расчетов:

Аналитический расчет

Аналитическое решение задачи для тонкой прямоугольной пластины построить сложно, поэтому задача упрощается, заменяя прямоугольный профиль на осесимметричную кольцевую пластину, тем самым получим качественное сравнение.
Прогиб – Вертикальное или горизонтальное перемещение точек, лежащих на одной оси нормально к плоскости элемента конструкции, под действием нагрузок, температур, ползучести материала.

Основное разрешающее уравнение изгиба пластины Софи Жермен:

Уравнение Софи Жермен для прогиба записывается в полярных координатах:

Граничные условия:

• Внутренний контур пластины жестко заделан:
  
• Внешний контур пластины свободен от нагрузок:
  

Решая уравнение Софи Жермен в полярных координатах и учитывая граничные условия пластины, было получено уравнение прогиба в искомой точке, где были выявлены максимальные перемещения (прогибы). Перемещения в точке максимального прогиба равны 1.26e-3 м.
В результате проведенных расчетов в программе ABAQUS для кольцевой пластины максимальные перемещения (прогиб) наблюдаются на внешнем контуре и равны 1.5e-3 м, что на 16% отличается от аналитического решения.

Заключение

По итогам данной работы можно утверждать:
1. Наименьшие прогибы (перемещения) были выявлены в варианте, где вакуумные чашки были расположены в 3 ряда и 3 столбца. Такой результат был достигнут за счет плотной компоновки вакуумных присосок.
2. Максимальные прогибы были выявлены в варианте, где вакуумная чашка была расположена в центре, её прогибы были близки к критическим (порядка 1мм), что в данной постановке задачи является не приемлемым.
3. В результате проведенных аналитических расчетов и расчетов в программе ABAQUS для упрощенной модели кольцевой пластины, качественное сравнение показывает что прогиб кольцевой пластины аналогичен прогибу квадратной и имеет тот же порядок.

Литература

1. Тимошенко С.П.,Войновский-Кригер С. Пластинки и оболочки. − М.:Государственное издательство физико-математической литературы. 1963. 635 с.
2. Тимошенко С.П. Курс теории упругости. − Киев. Издательство «Наукова думка». 1972. 507 с.
3. Бидерман В.Л. , Механика тонкостенных конструкций – Москва,“машиностроение” , 1977
4. Abaqus/CAE User's Manual, Dassault Systèmes, 2012
5. Рикардс Р.Б. , Метод конечных элементов в теории оболочек и пластин – Рига , 1988.
6. Теребушко О.И. , Основы теории упругости и пластичности, 1984.
7. Александров А.В. ,Потапов В.Д. ,.Изгиб тонких пластинок – Архангельск , 1998.
8. Жилин П.А., Основы Теории оболочек - Издательство Политехнического универститета, 2006.