Моделирование кабель-троса в задаче буксировки методом сосредоточенных параметров

БАКАЛАВРСКАЯ РАБОТА
Автор работы: А.Д. Степанов
Руководитель: к.т.н., зам главного конструктора бортовых систем ЗАО "Транзас" В. М. Амбросовский

Введение

Создание морских навигационных тренажеров, тренажеров маневрирования и управления движением судов, а так же создание отладочно-исследовательских стендов для настройки и исследования систем автоматического управления движением судов, требует наличия математических моделей, обеспечивающих моделирование судов и других морских подвижных объектов. Математические модели морских подвижных объектов, используемые в тренажерах и стендах должны обеспечивать необходимую точность и скорость формирования параметров движения морских подвижных объектов.

Одной из важных математических моделей, необходимых для морских тренажеров и стендов является математическая модель тросов или кабель-тросов, связывающих судно с буксируемым морским подвижным объектом или причалом.

Математические модели движения судов и описываются хорошо известными обыкновенными дифференциальными уравнениями. В отличии от этих моделей математическая модель связи, т.е. троса или кабель-троса, описывается уравнением в частных производных, что делает эту задачу более сложной.

Известны работы, в которых рассматривается задачи моделирования буксировочных тросов, связывающих буксир и буксируемое судно или задачи буксировки судном подводного аппарата. Однако в указанных работах не учитываются ограничения, связанные с конечной производительностью обычных компьютеров, используемых в тренажерах и стендах.

В настоящей работе рассмотрена задача разработки математической модели кабель-троса в задачи буксировки подводного заглубителя судном кабелеукладчиком для использования в морских тренажерах и стендах.

Постановка задачи

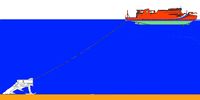
В работе рассматривается задача моделирования кабель-тороса, связывающего кабельное судно с подводным заглубителем, предназначенным для укладки кабеля с заглублением в грунт. Кабель-трос обеспечивает буксировку подводного заглубителя и подачу на него электропитания. Схематическое положение судна, подводного заглубителя и кабель-троса и их взаимодействие показано на рисунке:

Математическая модель движения кабельного судна в общем случае описывается обыкновенными нелинейными дифференциальными уравнениями вида \cite{lukomskiy}:

[math] m\underline{\dot{V}} = \underline{F}_{eng} + \underline{F}_{hidro} + \underline{F}_{aero} + \underline{F}_{Арх} + m\underline{g} + \underline{F}_{cable} [/math]

где [math] \underline{F}_{eng} [/math] --- сила тяги двигателей, [math]\underline{F}_{hidro} [/math] и [math] \underline{F}_{aero} [/math] --- сила гидродинамического и аэродинамического сопротивления соотвественно, [math] \underline{F}_{cable} [/math] --- сила, действующая со стороны кабель-троса. Аналогичным образом можно записать уравнение движения подводного заглубителя.

Уравнение описывающее положение кабель-троса и значение вектора силы, приложенного к подводному заглубителю, в общем случае имеет вид \cite{suhorukov_dinam}:

[math] \rho \dfrac{\partial^2\underline{u}(s,t)}{\partial{t}^2} = \dfrac{\partial{\underline{T}(s,t)}}{\partial{s}}+\rho \underline{F} [/math]

С учетом определяющего соотношения для силы натяжения [math] \underline{T} = f(\varepsilon)\dfrac{\partial{\underline{u}}}{\partial{s}} [/math], уравнение принимает вид волнового уравнения, являющимся частным случаем уравнения гиперболического типа.

[math] \rho \dfrac{\partial^2\underline{u}(s,t)}{\partial{t}^2} = \dfrac{\partial^2\underline{u}(s,t)}{\partial{s}^2}+\rho \underline{F} [/math]

Метод моделирования

В общем случае трос представляет собой весьма сложный нелинейный объект. Как было сказано, для решения поставленной задачи, можно использовать модель абсолютно гибкого растяжимого троса. Окружающей среда (морская вода) в рамках данной работы будет рассматриваться, как вязкая жидкость. Для конкретизации определяющих соотношений, надо принять следующие допущения:

• трос и любой его сегмент подчиняется закону Гука;
• можно пренебречь распределенными по длине троса крутящими моментами, которые возникают при действие на трос растягивающей силы\cite{kuvshin_monograf};
• обтекание кабель-троса потоком набегающей жидкости всегда считается ламинарным.

Эти предположения позволяют упростить уравнения и использовать метод сосредоточенных параметров.

Применение метода моделирования

Трос надо разбить на N элементов и N+1 узел. Нумерация узлов начинается с конца, соединенного с буксировщиком, первый элемент имеет номер N=1. Для разбиения выбирается длина [math]r_0 [/math], на основании которой вычисляется количество узлов, далее находим N по формуле [math] N = \dfrac{L}{r_0} [/math] и жесткость [math] k_i = \dfrac{k}{N} [/math]. Параметры узлов вычисляются следующим образом: масса [math] m_i = \dfrac{L\rho_{п}}{N+1}[/math], объем [math] V_i = r_0 S_{сечения} [/math] и находятся площадь поверхности [math] S_{\tau} = r_0\pi D [/math] и площадь сечения [math] S_{n}=r_0D [/math].

Уравнение движения узла

[math] m_i \underline{\dot{V_i}} = \underline{F}_{elast_{i-1}}+ \underline{F}_{elast_{i+1}} + \underline{F}_{Arch} + \underline{F}_{hidro} + m_{i}\underline{g} [/math]

Для [math]\underline{F}_{hidro} [/math] можно записать определяющее соотношение в виде:

[math] \underline{F}_{hidro} = C_{\tau}\frac{\rho{V_{\tau}}^2}{2}S_\tau\underline{\tau}+C_{n}\frac{\rho{V_{n}}^2}{2}S_n\underline{n} [/math]

Природа возникновения двух составляющих сил гидродинамического сопротивления различна: силы, направленные по направляющему вектору элемента троса [math] \underline{\tau} [/math] объясняются возникновением трения вязкой жидкости о поверхность тела, силы направленные перпендикулярно этому вектору появляются из-за перепада давлений при поперечном обтекании цилиндра. Коэффициент сопротивления давления [math] С_{n} [/math] зависит от числа Рейнольдса, определяемого по формуле [math] Re = \frac{V_nD}{\nu} [/math], и носит эксперементальный характер (см. \cite{prandtl} стр. 115, фиг. 58). Напротив, коэффициент сопротивления [math] C_{\tau} [/math] находится из решении задача Блазиуса по формуле (см. \cite{prandtl} стр. 113)

[math] \begin{cases} C_{\tau} = \dfrac{1.327}{\sqrt{\frac{V_{\tau}r_0}{\nu}}}, & Re = \frac{V_{\tau}r_0}{\nu} \lt 5\cdot10^5 \\ C_{\tau} = \dfrac{0.074}{\sqrt[5]{\frac{V_{\tau}r_0}{\nu}}}, & Re \gt 5\cdot10^6 \\ C_{\tau} = \dfrac{0.074}{\sqrt[5]{Re}}-\dfrac{1700}{Re}, & 5\cdot10^5 \lt Re \lt 5\cdot10^6 \end{cases} [/math]

Где [math] \nu [/math]--- кинематическая вязкость воды, [math] V_{\tau} [/math] --- скорость движения узла относительно воды.

Для [math]\underline{F}_{elast}[/math] определяющее соотношение выглядит следующим образом:

[math] \underline{F}_{elast}= \begin{cases} k\dfrac{\left|\underline{r}\right|- r_{0} }{\left| \underline{r}\right| }\underline{r}, &\text{if} \left| \underline{r}\right| - r_0 \geqslant 0 \\ 0, &\text{else} \end{cases} [/math]

Здесь [math] k [/math] --- жесткость рассматриваемого элемента, [math] r_0 [/math] --- его начальная длина, а [math] \left|\underline{r}\right| [/math] --- вектор, соединяющий соседние узлы. Жесткость можно найти по формуле

[math] k=\dfrac{ES_{сечения}}{r_0} [/math]

Таким образом, видно, что трос представляет собой упругий элемент реагирующий на растяжение согласно закону Гука и не реагирующий на сжатие.

Система координат

В задаче используется неподвижная система координат, связанная с землей.

• Ось X направлена на север (соотвествует базисному вектору [math] \underline{i} [/math]);
• Ось Y направлена против действия силы тяжести(соотвествует базисному вектору [math] \underline{j} [/math]);
• Ось Z образует с первыми двумя правую тройку (соотвествует базисному вектору [math] \underline{k} [/math]).

Список использованной литературы

• Л. Прандтль, О. Титьенс, Гидро- и аэродинамика Том 2, ОНТИ НКТП СССР, 1935.
• Г. Е. Кувшинов, Л. А. Наумов, К. В. Чупина, Системы управления глубиной погружения буксируемых объектов, Владивосток Дальнаука, 2005.
• А. Л. Сухоруков, Динамика тросовых систем, Санкт-Петербург, 2004.
• Ю. Г. Соловейчик, М. Э. Рояк, М. Г. Персова, Метод конечных элементов для скалярных и векторных задач, Новосибирск: НГТУ, 2007.
• Ю. И. Юдин, С. В. Пашенцев, В. В. Каян, Расчет усилий, действующих на объекты буксировки со стороны буксирной связи, Вестник МГТУ, том 16, №1, 2013.
• Iordan C. Matulea, Alexandru N stase, Nicoleta T lmaciu, Georgic  Slamnoiu, A.M. Goncalves-Coelho, On the equilibrium configuration of mooring and towing cables, Applied Ocean Research, 2008.
• Ю. А. Лукомский, В. М. Корчанов, Управление морскими подвижными объектами, Санкт-Петербург, 1996.
• А. Н. Крылов, Собрание трудов, т. IX. Теория корабля, ч.2. М.-Л.: изд-во АН СССР, 1936-1949.
• П. П. Кульмач, Якорные системы удержания плавучих объектов, издательство <<Судостроение>>, 1980.
• W.Raman-Nair, R. E. Baddour, Three-dimensional coupled dynamics of a buoy and multiple mooring lines: formulation and algorithm, Oxford University Press, 2002.