Моделирование кабель-троса в задаче буксировки методом сосредоточенных параметров

БАКАЛАВРСКАЯ РАБОТА
Автор работы: А.Д. Степанов
Руководитель: к.т.н., зам главного конструктора бортовых систем ЗАО "Транзас" В. М. Амбросовский

Введение

Создание морских навигационных тренажеров, тренажеров маневрирования и управления движением судов, а так же создание отладочно-исследовательских стендов для настройки и исследования систем автоматического управления движением судов, требует наличия математических моделей, обеспечивающих моделирование судов и других морских подвижных объектов. Математические модели морских подвижных объектов, используемые в тренажерах и стендах должны обеспечивать необходимую точность и скорость формирования параметров движения морских подвижных объектов.

Одной из важных математических моделей, необходимых для морских тренажеров и стендов является математическая модель тросов или кабель-тросов, связывающих судно с буксируемым морским подвижным объектом или причалом.

Математические модели движения судов и описываются хорошо известными обыкновенными дифференциальными уравнениями. В отличии от этих моделей математическая модель связи, т.е. троса или кабель-троса, описывается уравнением в частных производных, что делает эту задачу более сложной.

Известны работы, в которых рассматривается задачи моделирования буксировочных тросов, связывающих буксир и буксируемое судно или задачи буксировки судном подводного аппарата. Однако в указанных работах не учитываются ограничения, связанные с конечной производительностью обычных компьютеров, используемых в тренажерах и стендах.

В настоящей работе рассмотрена задача разработки математической модели кабель-троса в задачи буксировки подводного заглубителя судном кабелеукладчиком для использования в морских тренажерах и стендах.

Постановка задачи

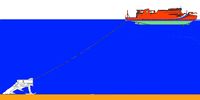
В работе рассматривается задача моделирования кабель-тороса, связывающего кабельное судно с подводным заглубителем, предназначенным для укладки кабеля с заглублением в грунт. Кабель-трос обеспечивает буксировку подводного заглубителя и подачу на него электропитания. Схематическое положение судна, подводного заглубителя и кабель-троса и их взаимодействие показано на рисунке:

Математическая модель движения кабельного судна в общем случае описывается обыкновенными нелинейными дифференциальными уравнениями вида \cite{lukomskiy}:

[math] m\underline{\dot{V}} = \underline{F}_{eng} + \underline{F}_{hidro} + \underline{F}_{aero} + \underline{F}_{Арх} + m\underline{g} + \underline{F}_{cable} [/math]

где [math] \underline{F}_{eng} [/math] --- сила тяги двигателей, [math]\underline{F}_{hidro} [/math] и [math] \underline{F}_{aero} [/math] --- сила гидродинамического и аэродинамического сопротивления соотвественно, [math] \underline{F}_{cable} [/math] --- сила, действующая со стороны кабель-троса. Аналогичным образом можно записать уравнение движения подводного заглубителя.

Уравнение описывающее положение кабель-троса и значение вектора силы, приложенного к подводному заглубителю, в общем случае имеет вид \cite{suhorukov_dinam}:

[math] \rho \dfrac{\partial^2\underline{u}(s,t)}{\partial{t}^2} = \dfrac{\partial{\underline{T}(s,t)}}{\partial{s}}+\rho \underline{F} [/math]

С учетом определяющего соотношения для силы натяжения [math] \underline{T} = f(\varepsilon)\dfrac{\partial{\underline{u}}}{\partial{s}} [/math], уравнение принимает вид волнового уравнения, являющимся частным случаем уравнения гиперболического типа.

[math] \rho \dfrac{\partial^2\underline{u}(s,t)}{\partial{t}^2} = \dfrac{\partial^2\underline{u}(s,t)}{\partial{s}^2}+\rho \underline{F} [/math]

Метод моделирования

В общем случае трос представляет собой весьма сложный нелинейный объект. Как было сказано, для решения поставленной задачи, можно использовать модель абсолютно гибкого растяжимого троса. Окружающей среда (морская вода) в рамках данной работы будет рассматриваться, как вязкая жидкость. Для конкретизации определяющих соотношений, надо принять следующие допущения:

• трос и любой его сегмент подчиняется закону Гука;
• можно пренебречь распределенными по длине троса крутящими моментами, которые возникают при действие на трос растягивающей силы\cite{kuvshin_monograf};
• обтекание кабель-троса потоком набегающей жидкости всегда считается ламинарным.

Эти предположения позволяют упростить уравнения и использовать метод сосредоточенных параметров.

Применение метода моделирования

Трос надо разбить на N элементов и N+1 узел. Нумерация узлов начинается с конца, соединенного с буксировщиком, первый элемент имеет номер N=1. Для разбиения выбирается длина [math]r_0 [/math], на основании которой вычисляется количество узлов, далее находим N по формуле [math] N = \dfrac{L}{r_0} [/math] и жесткость [math] k_i = \dfrac{k}{N} [/math]. Параметры узлов вычисляются следующим образом: масса [math] m_i = \dfrac{L\rho_{п}}{N+1}[/math], объем [math] V_i = r_0 S_{сечения} [/math] и находятся площадь поверхности [math] S_{\tau} = r_0\pi D [/math] и площадь сечения [math] S_{n}=r_0D [/math].

%==Модель лука с упругими стержнями== %==Эксперименты== %==Результаты==