КП: Корпоративный чат

А.М. Кривцов > Теоретическая механика > Курсовые проекты 2014 > Моделирование колебаний (пружина + груз) (JS)

---

Фигуры Лиссажу

Курсовой проект по Теоретической механике

Исполнитель: Киселев Павел

Группа: 08 (23604)

Семестр: весна 2014

Аннотация проекта

Проект направлен на изучение колебания тела на пружине и моделирование этого процесса на языке JavaScript

Постановка задачи

- Изучить колебания тела на пружине

- Написать программу, моделирующую колебания системы из n тел и (n+1) пружин в горизонтальной плоскости

Общие сведения по теме

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.
Для тонкого растяжимого стержня закон Гука имеет вид:
[math] F = k \ Delta\ (l) [/math]
Рассмотрим систему тел:
[math] m \ddot{u} = F_{n+1} - F_n [/math] ( 2-й закон Ньютона )
[math]F_{n+1} = C \ (u_{n+1} - u_n) [/math] ; [math]F_n = C \ (u_n - u_{n-1}) [/math]

где Cx и Cy - жесткости пружин, m - масса грузика, B - вязкость среды
Складываемые колебания имеют вид:
[math] x = A_x \cos (\omega_xt+\alpha_x) [/math]
[math] y = A_y \cos (\omega_yt+\alpha_y) [/math]
Частоты колебаний определяются как [math]\omega_x = \sqrt{\frac{C_x}{m}},\omega_y = \sqrt{\frac{C_y}{m}}[/math]

Результат

Результатом работы стала программа, написанная на языке JavaScript. Возможности программы:
- Выбор простого либо сложного движения( под простым движением подразумевается учитывание только силы упругости вдоль оси, в сложном же - учитывается и сила упругости, и сила деформации пружины действующая под углом)
- Возможность изменения массы, жесткости пружин по оси абцисс и ординат, вязкость среды
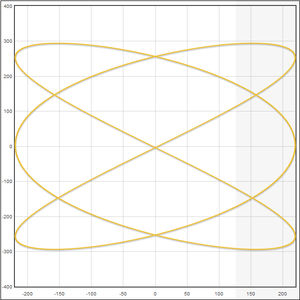
- Визуальное отображение траектории движения грузика с возможностью очистки графика
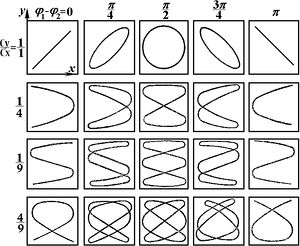
Моделирование фигур Лиссажу методом пружин

Ссылки по теме

Моделирование фигур Лиссажу методом пружин
Фигуры Лиссажу

См. также

• Справочная информация
• Курсовые проекты 2013
• Курсовые проекты 2012
• JavaScript-программирование