Корреляции перемещений в кристаллах (компьютерное моделирование)

Расчеты: Панченко Артём

Корреляция колебаний

ГЦК

Рассчитаны корреляции [math]\mathbf{A}\mathbf{A_\alpha}[/math], [math]\mathbf{u}\mathbf{u}[/math], [math]\mathbf{u}\mathbf{u_\alpha}[/math] в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (по другой связи), ось аппликат по векторному произведению абсциссы и ординаты. Тензоры диагональны с точность [math]10^{-3}[/math].

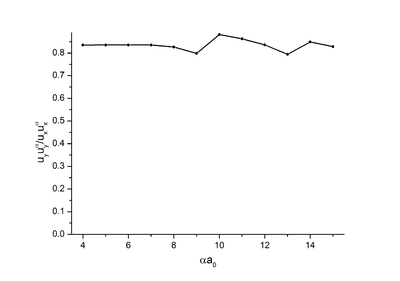
При отсутствии внешних напряжений зависимость [math]\mathbf{u}\mathbf{u_\alpha}[/math] от ширины потенциальной ямы для потенциала морзе отсутствует (Рис.1.1).

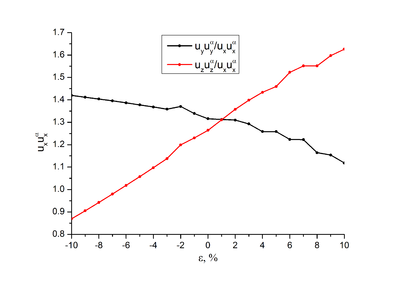
При постоянной ширине потенциальной ямы компоненты [math]\mathbf{u}\mathbf{u_\alpha}[/math] зависят от гидростатической деформации линейно, при этом [math]\mathbf{j}\mathbf{j}[/math] компонента с расширением убывает, а [math]\mathbf{k}\mathbf{k}[/math] возрастает (Рис.1.2).

Рис. 1.1. Зависимость [math]\mathbf{u}\mathbf{u_\alpha}[/math] от [math]\varepsilon[/math].

Рис. 1.2. Зависимость [math]\mathbf{u}\mathbf{u_\alpha}[/math] от [math]{\alpha}{a_0}[/math].

2D Треугольная

Рассчитаны корреляции [math]\langle\mathbf{A}\mathbf{A}\rangle[/math], [math]\langle\mathbf{u}\mathbf{u}\rangle[/math], [math]\langle\mathbf{u}\mathbf{u}'\rangle[/math] в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (векторное произведение оси абсцисс и вектора перпендикулярного плоскости). Тензоры диагональны с точностью [math]10^{-3}[/math].

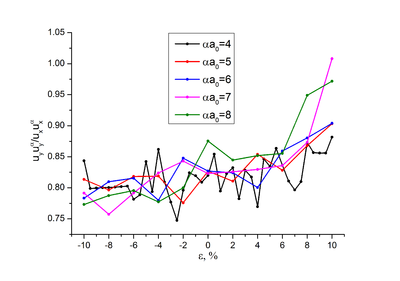
Отношение перпендикулярной компоненты корреляции [math]\langle\mathbf{u}\mathbf{u}'\rangle[/math] к продольной увеличивается при растяжении, и не имеет выраженной зависимости от [math]{\alpha}{a_0}[/math] (Рис.1.3).

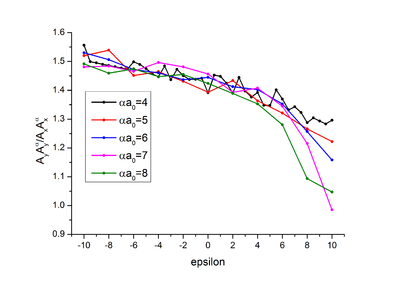
Отношение перпендикулярной компоненты корреляции [math]\langle\mathbf{A}\mathbf{A}\rangle[/math] к продольной уменьшается при растяжении, можно заметить слабое уменьшение отношение с ростом [math]{\alpha}{a_0}[/math] (Рис.1.4).

Рис. 1.3. Зависимость [math]\langle\mathbf{u}\mathbf{u}'\rangle[/math] от [math]\varepsilon[/math] при различных [math]{\alpha}{a_0}[/math].

Рис. 1.4. Зависимость [math]\langle\mathbf{A}\mathbf{A}\rangle[/math] от [math]\varepsilon[/math] при различных [math]{\alpha}{a_0}[/math].

Проведем анализ графиков Рис. 1.3 - 1.4 (А.М. Кривцов).

Величина	Значения			Источник	Комментарий
[math]\varepsilon[/math]	-5%	0	5%	Рис. 1.3 - 1.4	деформация
[math]p = \langle A_y A_y\rangle/\langle A_x A_x\rangle[/math]	1.48	1.42	1.36	Рис. 1.4	отношение поперечной составляющей тензора [math]\langle\mathbf{A}\mathbf{A}\rangle[/math] к продольной
[math]q = \langle u_y u_y'\rangle/\langle u_x u_x'\rangle[/math]	0.810	0.825	0.830	Рис. 1.3	отношение поперечной составляющей тензора [math]\langle\mathbf{u}\mathbf{u}'\rangle[/math] к продольной
[math]\beta = \langle u_x u_x'\rangle/\langle u_x^2\rangle[/math]	0.716	0.706	0.679	расчет	относительная продольная корреляция перемещений
[math]\gamma = \langle u_y u_y'\rangle/\langle u_y^2\rangle[/math]	0.580	0.582	0.564	расчет	относительная поперечная корреляция перемещений

Связь параметров [math]p,q[/math] и [math]\beta,\gamma[/math] определяется формулами

[math]p = \frac{1-\gamma}{1-\beta}, \quad q = \frac{\gamma}{\beta}; \qquad \beta = \frac{p-1}{p-q}, \quad \gamma = q\,\frac{p-1}{p-q}.[/math]

На основании данных таблицы можно сделать следующие выводы.

• В рассмотренном интервале деформаций (от -5% до 5%) зависмости [math]p[/math] и [math]q[/math] от деформаций можно считать линейными.
• Зависимость [math]\beta[/math] и [math]\gamma[/math] от деформаций оказывается заметно нелинейной.
• В целом величины [math]p,q[/math] и [math]\beta,\gamma[/math] в рассматриваемом интервале деформаций меняются незначительно.
• Относительная поперечная корреляция [math]\gamma[/math] несколько меньше, чем относительная продольная [math]\beta[/math], что представляется разумным.
• Значения относительных корреляции [math]\beta[/math] и [math]\gamma[/math] сравнимы с единицей, что странно. Получается, что перемещения ближайших частиц сильно коррелируют. Не связано ли это с использованием термостата или какого-то другого вычислительного приема?

Отметим, что согласно формуле [math]p = (1-\gamma)/(1-\beta)[/math], тензор [math]\langle\mathbf{A}\mathbf{A}\rangle[/math] будет близок к шаровому ([math]p \approx 1[/math]) в одном из двух случаев:

• Относительные корреляции малы: [math]|\beta|\ll1[/math], [math]|\gamma|\ll1[/math].
• Относительные корреляции близки: [math]\beta\approx\gamma[/math].

В рассматриваемом случае относительные корреляции не малы, и, хоть и не очень значительно, но различаются, что приводит к существенному отклонению формы тензора [math]\langle\mathbf{A}\mathbf{A}\rangle[/math] от шаровой ([math]p \approx 1.4[/math]).

Тепловое расширение

Для определения коэффициента теплового расширения использовалось два подхода: при постоянном объёме и постоянном давлении (с помощью баростата давление приближалось к нулю).

ГЦК

Леннард-Джонс

Постоянный объём

ГЦК кристалл 30x30x30 ГЦК ячеек (??? частиц), периодические граничные условия, релаксация системы в течении 10*Tp, Tp = T0p/200, полное время определения давления 20*Tp, время определения точек среднего 3*Tp. Температура системы от 1e-7*Tk, до 1.9e-6*Tk. На первом шаге задаются начальные скорости согласно нормальному распределению, затем система релаксирует, и далее вычисляется давление на основе метода Кривцова-Кузькина.

Коэффициент теплового расширения определённый по первой точке: 0.127474, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.39%.

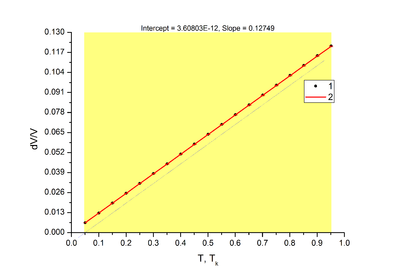
Коэффициент теплового расширения определённый по наклону (Рис.1): 0.12749, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.38%.

Рис. 1. Зависимость объёмной деформации от температуры. 1 - Значение определённое при усреденении по всему интервалу, 2 - усреднение по малым интервалам