Michael Szelwis: "Particle-reinforced composites simulated by cohesive discrete elements"

Microscopic photograph the investigated ceramic-polymer-composite

For the research on a ceramic-polymer-composite (TiO2 in a PMMA matrix) with very high content of ceramic particles a numerical model is being investigated. To simulate the nonlinear deformation due to indentation a discrete element approach has been chosen with each ceramic particle being represented by one particle in the simulation. Several models for the interaction of the ceramic particles with one another as well as with the polymeric matrix, such as cohesion and physical bonds, are being tested using the software package EDEM and are also being compared with experimental results.

Previous Work

Specimen of previous work with bonds representing polimeric matrix

Simulating the mechanical behaviour of the investigated material, Hertzian contacts between the particles were combined with EDEM's default bond model representing the polymeric matrix. Indentation tests revealed qualitative accordance to experimental results within the region of elastic deformation of the specimen. It was shown that a stiffer material used for the polymeric matrix, which has been modelled by bonds with larger Young's modulus, leads to a higher stiffness of the specimen.

Performing large deformations within the simulation, the created specimen deforms elastically until the stress in the bonds reaches a previously defined threshold value. Bond breakage occurs after exceeding this threshold and the interaction between the particles becomes purely Hertzian. For this region where deformation becomes plastic, the stress-strain behaviour of the model doesn't represent the real material's behaviour anymore.

Representing Polymer by Cohesion of Particles

Cohesion model (40,000 pts): specimen during indentation; particles colored with respect to compressive force; specimen has periodic boundaries in X- and Y-direction

Cohesion model (40,000 pts): surface of specimen after indentation

Cohesion model (40,000 pts): indentation-force over time ! THIS IS A DRAFT AND DOES NOT CONTAIN LABELING !

The main problem of using bonds simulating the material's plastic behaviour is that in this case, particle rearrangement always goes along with the breakage of bonds and therefore with a drastic change of the simulated material's properties. Plastic deformation is generally associated with so-called dislocation movement where the atoms of the material rearrange during deformation due to imperfections in the crystal structure. During this process energy dissipates but the mechanical properties of the material remain more or less unchanged. Therefore, it would be desirable for a model which is supposed to represent the investigated ceramic-polymer-composite, to contain consistent particle interactions before and after the relocation of particles.

The Cohesion of primary particles is an implemented contact model in EDEM in which the simulated attractive force between particles does not change with thier relocation. Also, it represents how we generally understand the constitution of substances on an atomic scale. Consequently, it might be suitable to model the mechanical properties of the investigated material including elastic as well as plastic behaviour. Nevertheless, it is questionable if this approach can predict the properties of the material when used on a very large scale where each particle in the simulation represents one ceramic particle embedded in a matrix of polymer.

Details of Simulation (DRAFT)

To keep the calculations as simple as possible first simulations were run using the default Hertz-Mindlin contact model as well as the model for particle cohesion which are provided within EDEM. In this case the Hertz-Mindlin-Force between two equivalent particles in contact gets calculated as follows:

[math]F_{HM}(\delta_n) = \frac{2}{3}\times\frac{E}{(1-\nu^2)}\times\sqrt{R/2}\times\delta_n^{\frac{3}{2}}[/math]

with [math]E[/math] and [math]\nu[/math] being the Young's Modulus and the Poisson's Ratio of the particles, [math]R[/math] being thier radius and [math]\delta_n[/math] being the normal overlap assuming the particles remain spherical when in contact. Considering this assumption, the Particle Cohesion calculates:

[math]F_{C}(\delta_n) = k\times\pi\times(R^2-(R-\delta_n/2)^2)[/math]

with [math]k[/math] being a constant parameter of the cohesive force (also referred to as energy density).

This leads to the total force between two interacting particles of

[math]F_{Total}(\delta_n) = -\frac{1}{4}\pi k\delta_n^2+\frac{\sqrt{2R}\times E}{3(1-\nu^2)}\delta_n^{\frac{3}{2}}+\pi k R\delta_n[/math]

If attractive and repulsive forces are of the same magnitude the particle contact reaches an equilibrium state with an equilibrium overlap [math]\delta_{n,eq}[/math]. Besides the trivial solution [math]\delta_{n,eq1}=0[/math] there might be found a second solution for which the particle contact becomes stable. Unfortunately, this second equilibrium distance [math]\delta_{n,eq2}[/math] can not be adjusted to [math]0\lt \delta_{n,eq2}\lt R[/math] which would be suitable for the intended simulations. Besides, this is the only range for which EDEM calculates the particle forces which means that with the indicated formulas, an equilibrium distance of two interacting particles can never be reached.

While a stable configuration for indentation experiments can still be reached (high friction between particles prevents them from collapsing) the simulation of a bending experiment will not be possible. To eliminate this problem a modified cohesion model with a larger radius for the calculation of cohesive forces than the particle radius will be considered in future simulations (see below).

Further characteristics of simulation:

• 10,000/40,000 particles
• Periodic boundaries
• Quasi-2D
• Close packing (0.63)

Results

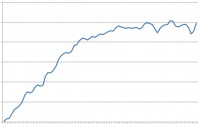
Simulations revealed the possibility to qualitatively predict a material's response due to indentation by approximating the structure of the investigated material using discrete particles applying Hertzian contact laws, linear cohesion as well as linear friction. Furthermore, this concept is comparable to how deformation processes are generally explained on an atomic scale which emphasizes the consideration of this approach. The fact that the particles in the simulation being of magnitues larger than real atoms does not seem to have an impact on the results even though it involves a certain coarseness of the plastic area which distinguishes itself in particle relocation (see force-displacement curves).

Next Steps within this Work

• Quantitative comparison of the results with experimental data
• Realizing a varying relevant radius for the calculations of cohesive- and contact forces (at the moment it is impossible to reach equilibrium state)
• Performing bending test (with new model of varying radii)
• Ensuring the results do not change quantitively by increasing the number of used particles
• Examining the suitability using the cohesive model for the investigation of hirarchic materials