Michael Szelwis: "Particle-reinforced composites simulated by cohesive discrete elements"

Microscopic photograph the investigated ceramic-polymer-composite

For the research on a ceramic-polymer-composite (TiO2 in a PMMA matrix) with very high content of ceramic particles a numerical model is being investigated. To simulate the nonlinear deformation due to indentation a discrete element approach has been chosen with each ceramic particle being represented by one particle in the simulation. Several models for the interaction of the ceramic particles with one another as well as with the polymeric matrix, such as cohesion and physical bonds, are being tested using the software package EDEM and are also being compared with experimental results.

Previous Work

Specimen of previous work with bonds representing polimeric matrix

Simulating the mechanical behaviour of the investigated material, Hertzian contacts between the particles were combined with EDEM's default bond model representing the polymeric matrix. Indentation tests revealed qualitative accordance to experimental results within the region of elastic deformation of the specimen. It was shown that a stiffer material used for the polymeric matrix, which has been modelled by bonds with larger Young's modulus, leads to a higher stiffness of the specimen.

Performing large deformations within the simulation, the created specimen deforms elastically until the stress in the bonds reaches a previously defined threshold value. Bond breakage occurs after exceeding this threshold and the interaction between the particles becomes purely Hertzian. For this region where deformation becomes plastic, the stress-strain behaviour of the model doesn't represent the real material's behaviour anymore.

Representing Polymer by Cohesion of Particles

Cohesion model: surface of specimen after indentation

Cohesion model: indentation-force over time !!! THIS IS A DRAFT AND DOES NOT CONTAIN LABELING !!!

The main problem of using bonds simulating the material's plastic behaviour is that in this case, particle rearrangement always goes along with the breakage of bonds and therefore with a drastic change of the simulated material's properties. Plastic deformation is generally associated with so-called dislocation movement where the atoms of the material rearrange during deformation due to imperfections in the crystal structure. During this process energy dissipates but the mechanical properties of the material remain more or less unchanged. Therefore, it would be desirable for a model which is supposed to represent the investigated ceramic-polymer-composite, to contain consistent particle interactions before and after the relocation of particles.

The Cohesion of primary particles is an implemented contact model in EDEM in which the simulated attractive force between particles does not change with thier relocation. Also, it represents how we generally understand the constitution of substances on an atomic scale. Consequently, it might be suitable to model the mechanical properties of the investigated material including elastic as well as plastic behaviour. Nevertheless, it is questionable if this approach can predict the properties of the material when used on a very large scale where each particle in the simulation represents one ceramic particle embedded in a matrix of polymer.

Details of Simulation (!! DRAFT !!)

To keep the calculations as simple as possible first simulations were run using default models of Hertz-Mindlin-contact as well as of particles cohesion which are provided within EDEM. In this case the Hertz-Mindlin-Force between two equivalent particles in contact gets calculated as follows:

[math]F_{HM}(\delta_n) = \frac{2}{3}\times\frac{E}{(1-\nu^2)}\times\sqrt{R/2}\times\delta_n^{\frac{3}{2}}[/math]

with [math]E[/math] and [math]\nu[/math] being the Young's Modulus and the Poisson's Ratio of the particles, [math]R[/math] being thier radius and [math]\delta_n[/math] being the normal overlap assuming the particles remain spherical when in contact. Considering this assumption, the Cohesion calculates:

[math]F_{C}(\delta_n) = k\times\pi\times(R^2-(R-\delta_n/2)^2)[/math]

with [math]k[/math] being a constant parameter of the cohesive force (also referred to as energy density).

This leads to a total force between two interacting particles of

[math]F_{Total}(\delta_n) = -\frac{1}{4}\pi k\delta_n^2+\frac{\sqrt{2R}\times E}{3(1-\nu^2)}\delta_n^{\frac{3}{2}}+\pi k R\delta_n[/math]

• 40,000 particles
• Periodic boundaries
• Quasi-2D
• Close packing (0.63)

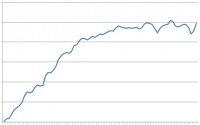
Results (!! DRAFT !!)

• Qualitative accordance with real material's behaviour during indentation

Outlook

• Quantitative comparison of the results with experimental data
• Realizing a varying relevant radius for the calculations of cohesive- and contact forces
• Performing bending test (with model of varying radii)
• Ensuring the results do not change (qualitively as well as quantitively) by increasing the number of used particles
• Examining the suitability using the cohesive model for the investigation of hirarchic materials