Выполнил: Клак М.А.
Научный руководитель: Иванова Е.А.
В современных конструкциях и сооружениях большое применение имеют детали, являющиеся относительно длинными и тонкими стержнями. Поведение таких стержней под действием осевой сжимающей силой оказывается иным, чем поведение коротких стержней при сжатии. При достижении силой некоторого критического значения прямолинейная форма стержня становится неустойчивой, и стержень начинает искривляться. Это явление называется потерей устойчивости.
Постановка задачи[править]
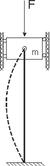
Рассматривается первоначально прямолинейный безынерционный стержень с массой на верхнем конце. Решается задача о потери устойчивости этого стержня в случае действия на него динамической сжимающей силы.
Уравнения динамики стержня[править]
[math]\underline{N}'(s, t) = 0[/math]
[math]\underline{M}'(s, t) + \underline{R}'(s, t)\times \underline{N}(s, t) = 0[/math]
Определяющее уравнение для момента
[math]\underline{M} = (C_3-C_1)(\underline{t}\cdot\underline{\underline{P}}^T\cdot\underline{\Phi})(\underline{\underline{P}}\cdot\underline{t}) + C_1\underline{\Phi}[/math]
Вектора деформации
Связь вектор деформации изгиба кручения с тензором поворота
[math]\underline{\underline{P}}'=\underline{\Phi} \times \underline{\underline{P}}[/math]
Вектор деформации растяжения сдвига
[math]\underline{\varepsilon} = \underline{R}'-\underline{\underline{P}}\cdot\underline{t}[/math]
Задача решается в классической теории стержней: [math]\underline{\varepsilon}=0[/math], следовательно: [math]\underline{R}'=\underline{\underline{P}}\cdot{t}[/math]
Граничные условия
Условие жесткой заделки на нижнем конце:
Отсутствие перемещений
[math]\underline{R}|_{s=0}=0[/math] ,
Отсутствие поворота
[math]\underline{\underline{P}}|_{s=0}=\underline{\underline{E}}[/math]
Условия на верхнем конце стержня:
уравнение движения груза: [math]m(\underline{t}\cdot\underline{R}^{\cdot\cdot})|_{s=l}=-F(t)-mg-(\underline{t}\cdot\underline{N}|_{s=l})[/math]
Отсутствие перемещений в плоскости
[math]\underline{R}|_{s=l}\cdot(\underline{\underline{E}}-\underline{t}\underline{t})=0[/math]
Возникновение сил реакций
[math]\underline{N}|_{s=l}\cdot(\underline{\underline{E}}-\underline{t}\underline{t})=\underline{F}^*[/math]
Т.к. груз шарнирно прикреплен к стержню
[math]\underline{M}|_{s=l}=0[/math]
Решение уравнений статики стержня[править]
Вектор силы [math]\underline{N}=\underline{N}|_{s=l}[/math]
Вектор деформации: [math]\underline{\Phi}=\underline{R}'\times \underline{R}''[/math]
Вектор момента: [math]\underline{M}=C_1\underline{\Phi}[/math], принимая во внимание ранее полученное выражение для вектора деформации [math]\underline{M}=C_1\underline{R}'\times\underline{R}''[/math]
Доказывается, что конфигурация изогнутого стержня - плоская
[math]\underline{\underline{P}}=\underline{\underline{P}}(\psi\underline{b})[/math]
Тогда можно найти радиус вектор [math]\underline{R}'[/math]
[math]\underline{R}'=cos\psi\underline{t}+sin\psi\underline{n}[/math]
В результате итоговое выражение для момента будет выглядеть [math]\underline{M}=C_1\psi\underline{b}[/math]
Краевая задача для [math]\psi[/math][править]
Дифференциальное уравнение
[math]C_1\psi(s)+(\underline{n}\cdot\underline{N})cos\psi-(\underline{N}\cdot\underline{t})sin\psi=0[/math]
Граничные условия для переменной [math]\psi[/math]:
[math]\psi|_{s=0}=0[/math]
[math]\psi'|_{s=l}=0[/math]
Введем новые обозначения: [math]\underline{N}=N\underline{n}[/math],
[math]\underline{e}\cdot\underline{n}=-sin\beta[/math],
[math]\underline{e}\cdot\underline{t}=-cos\beta[/math]
Произведем замену переменных
[math]\tilde\psi~=\psi-\beta[/math]
Краевая задача в новых обозначениях:
<nath>C_1\tilde\psi(s)+Nsin\tilde\psi=0</math>
Граничные условия для новой переменной [math]\tilde\psi[/math]:
[math]\tilde\psi|_{s=0}=-\beta, \tilde\psi'|_{s=l}=0[/math]
Первый интеграл
[math]\tilde\psi=\pm2\sqrt{\frac{N}{C_1}[sin^2\frac{\tilde\psi_l}{2}-sin^2\frac{\tilde\psi}{2}]}, [/math]где [math]\tilde\psi_l=\tilde\psi|_{s=l}[/math]
[math]\underline{N}=N\underline{e} =\gt N \gt 0 =\gt sin^2\frac{\tilde\psi_l}{2}-sin^2\frac{\tilde\psi}{2} \ge 0[/math]
Тогда можем сделать замену:
[math]sin\theta=\frac{sin^2\frac{\tilde\psi}{2}}{sin^2\frac{\tilde\psi_l}{2}}[/math]
Дифференциально уравнение для новой переменной: [math]\theta'=\frac{N}{C_1}[1-sin^2\xi sin^2\theta][/math]
Используем оставшееся гр. условие и получим: [math]\theta|_{s=0}=\theta_0[/math]
Тогда решение задачи в квадратурах:
[math]\sqrt{\frac{N}{C_1}}s=\int_{\theta_0}^{\theta}\frac{d\tau}{\sqrt{1-sin^2\xi sin^\tau}}[/math]
Критическая сила[править]
Пусть полученный ранее интеграл - интеграл от параметра
[math]\sqrt{\frac{N}{C_1}}s=J(\xi)[/math], где [math]J(\xi)=\int_{\theta_0}^{\frac{\pi}{2}}\frac{d\tau}{\sqrt{1-sin^2\xi sin^\tau}}[/math]
[math]J(\xi)[/math] принимает минимальное значение при [math] \xi=0 [/math], тогда интеграл равен: [math]\frac{\pi}{2}-\theta_0[/math]
Следовательно [math]\sqrt{\frac{N}{C_1}}s \ge J(0)[/math], тогда значение критической силы [math]N_cr=\frac{(\pi-2\theta_{0}^{cr})C_1}{4 l^2}[/math]
[math]ctg\theta_{0}^{cr}=\frac{\pi}{2}-\theta_{0}^{cr}[/math]