КП: Диск Эйлера

А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Диск Эйлера

---

Курсовой проект по Теоретической механике

Исполнитель: Соколов Алексей

Группа: 07 (20510)

Семестр: весна 2013

Аннотация проекта

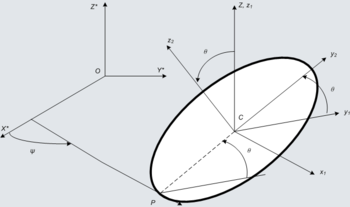
Диск Эйлера – это твёрдое цилиндрическое тело, имеющее единственную точку контакта с горизонтальной поверхностью, по которой он одновременно и катится, и вращается. Этой простой механической системе присущи две любопытные особенности — быстрое возрастание звуковой частоты в процессе контакта диска и поверхности на финальном этапе движения, а также последующая внезапная остановка движения. Эти эффекты может наблюдать каждый, раскрутив на столе обыкновенную монету: «потеряв равновесие», монета окажется лежащей на столе плашмя, при этом финальная стадия ее движения, когда ее плоскость почти горизонтальна, сопровождается характерным «дрожанием». Однако физическое объяснение этого своеобразного поведения оказалось сложной задачей, решение которой еще требует дальнейших экспериментальных и теоретических исследований.

Решение

Запишем кинетический момент сиcтемы:
[math] \dot{\b{\b{K}}} = \dot{ \left( \b{\b{O}} \cdot \b{w} \right) } = \b{M} [/math]
[math] \dot{\b{\b{K}}} = \Theta_{12} \b{n} \times \dot{\b{n}} + \Theta_3 \dot{ \left(\Omega \b{n} \right) } [/math]
Положим
[math] \eta = \b{k} \cdot \b{n} = \cos( O) [/math]
[math] \epsilon = \b{k} \times \b{n} = \sin( O) [/math]
Имеем далее
[math]\left\{ \begin{array}{rcl} \b{a} \perp \b{k} \times \b{n} \\ \b{a} \perp \b{n} \\ \end{array} \right. [/math]

Из этого следует:
[math] \b{a} \parallel \left[ \b{n} \times ( \b{k} \times \b{n} \right ] [/math]
Имеем
[math] \b{n} \times ( \b{k} \times \b{n} ) = \b{k} ( \b{n} \cdot \b{n}) - \b{n} (\b{n} \cdot \b{k}) = \b{k} - \eta \b{n} [/math]
Таким образом можем представить вектор [math] \b{a} [/math] следующим образом:
[math] \b{a} = \lambda( \b{k} - \eta \b{n}) [/math]
Имеем далее:
[math] a^2 = \lambda^2(1 - \eta^2) = \lambda^2 \epsilon [/math]
Таким образом
[math] \lambda = \frac{a}{ \sqrt{1 - \eta^2} } [/math]
Недтрудно понять что вектор [math] \b{a} [/math] в таком случае записывается в следующем виде:
[math] \b{a} = \frac{a}{ \sqrt{1 - \eta^2} } ( \b{k} - \eta \b{n}) [/math]
Имеем далее:
[math] \frac{ \b{a} } {a} = \frac{ \b{k} - \eta \b{n} } { \left| \b{k} - \eta \b{n} \right| } [/math]
Получаем таким образом:
[math] \b{a} = \frac{a}{\epsilon} (\b{k} - \eta \b{n}) [/math]
Теперь запишем соотношения для сил и моментов:
[math] m \dot{\b{r}} = m \b{g} + \b{N} = (N - mg) \b{k} [/math]
[math] \dot{ \left( \b{\b{O}} \cdot \b{w} \right) } = \b{a} \times \b{N} [/math]
[math] \b{N} = N \b{k} [/math]
Таким образом имеем:
[math] \b{a} \times \b{N} = \frac{a \eta}{ e} N \b{k} \times \b{n} [/math]
В результате получаем систему:

Ссылки по теме

• Динамика твердого тела: примеры (диск Эйлера)

См. также

• Справочная информация
• Курсовые проекты 2012
• Курсовые проекты 2013