Течение двухфазной жидкости
Моделирование течения двухфазной жидкости
Исполнители: Буковская Карина
Одним из методов интенсификации работы нефтяных и газовых скважин является гидроразрыв пласта.Гидравлический разрыв пласта заключается в формирование трещин в массивах газо-, нефте-, водонасыщенных и других горных породах под действием подаваемой в них под давлением жидкости. Операция проводится в скважине для повышения дебита за счет разветвленной системы дренирования, полученной в результате образования протяженных трещин. Реализация гидроразрывов пластов на газовых скважинах стала возможной с появлением насосных агрегатов, обеспечивающих скорость закачки 3–4 куб. м/мин при давлении 100 МПа. При закачке в скважину рабочей жидкости с высокой скоростью на ее забое создается высокое давление. Если оно превышает горизонтальную составляющую горного давления, то образуется вертикальная трещина. В случае превышения горного давления формируется горизонтальная трещина. В качестве рабочей жидкости, как правило, используют загущенные жидкости на водной или углеводородной основе. Вместе с рабочей жидкостью закачивают закрепляющий агент (песок или твердый материал фракции 0,5–1,5 мм), заполняющий трещину и препятствующий ее смыканию. При применении загущенной жидкости за счет снижения ее утечек в пласт можно поднять забойное давление при значительном снижении скорости закачки и за счет песконесущей ее способности транспортировать закрепляющий агент по всей длине трещины.
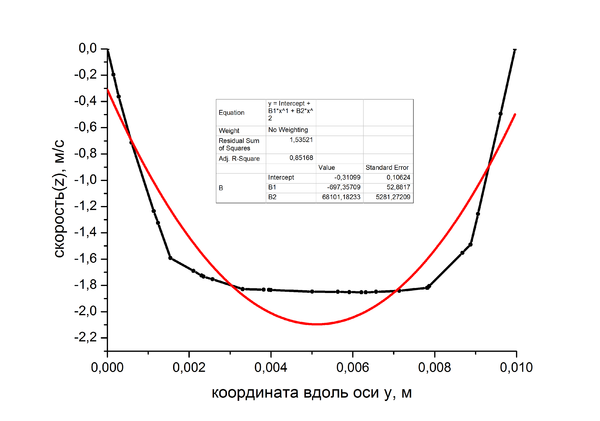
В данной работе проведено моделирование двухфазной жидкости (несущая жидкость и проппант) с использованием алгоритма совмещения пакетов ANSYS FLUENT и EDEM (Coupling Module). Целью является установление зависимости вязкости смеси от концентрации частиц проппанта. Для этого измеряются скорости модельной смеси при различных концентрациях твердой фазы и различных давлениях. Рассматривается установившееся течение несжимаемой жидкости с постоянной вязкостью в тонкой цилиндрической трубке круглого сечения под действием постоянной разности давлений. Если предположить, что течение будет ламинарным и одномерным, то уравнение решается аналитически, и для скорости получается параболический профиль (часто называемый профилем Пуазейля) — распределение скорости в зависимости от расстояния до оси канала
v=(ρ_1-ρ_1)/4μl(1-r^2)
v — скорость жидкости вдоль трубопровода, м/с;r — расстояние от оси трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м. Закон Хагена — Пуазейля, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения.
Q=(π∙d^4∙(ρ_(1-) ρ_2))/(128∙μ∙l)=(π∙r^4∙(ρ_(1-) ρ_2))/(8∙μ∙l)
Q — расход жидкости в трубопроводе, м³/с;d — диаметр трубопровода, м;r — радиус трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м.
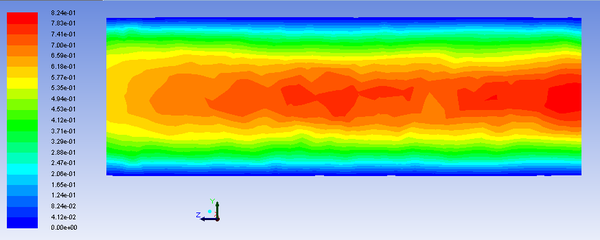
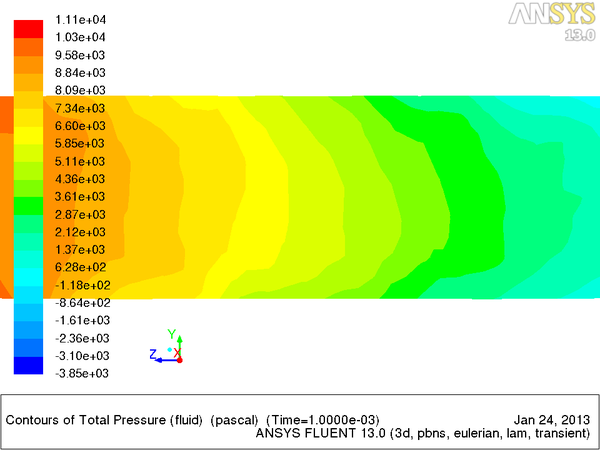
Расчет течения Пуазейля во FLUENT Рассматривается цилиндрическая трубка с диаметром основания 10мм ,длиной 30мм. В качестве жидкости было выбрано подобие воды с вязкостью в 20 раз больше воды (0.2 кг/(м*с)). Граничные условия:на входе давление 1000 Па,на выходе 0 Па. Сходимость решения достигалась за 70 итераций.
- график показателей скорости
- график показателей давления
Расчет Coupling Module EDEM
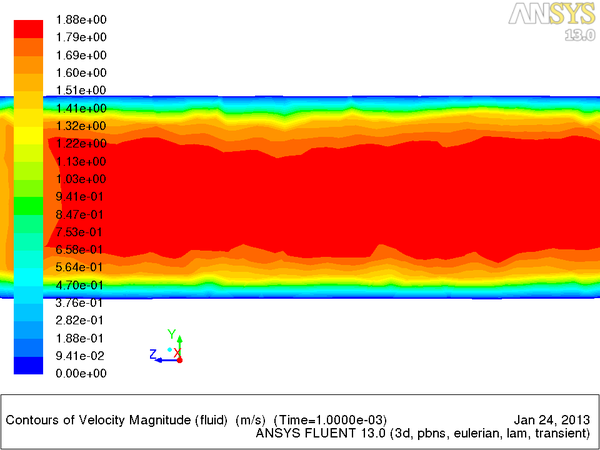
Была выбрана трубка тех же геометрических размеров,параметры жидкости неизменные.Граничные условия на входе скорость 1.5 м/с ,на выходе 0 Па. Количество частиц 5% от объема цилиндра (28125 частиц)
размер : 1*10e-4, плотность 2500 кг/м^3.
размеры частиц
rad.0.0003 m, mass 2.82743e-07 kg,volume 1.13097e-10 m^3,velocity 1*10e-4
заданы периодические граничные условия.
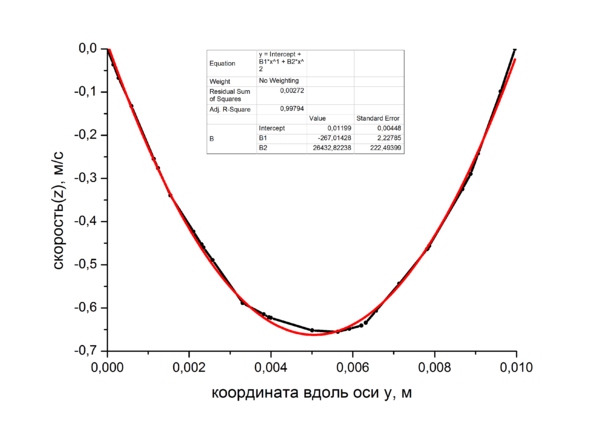
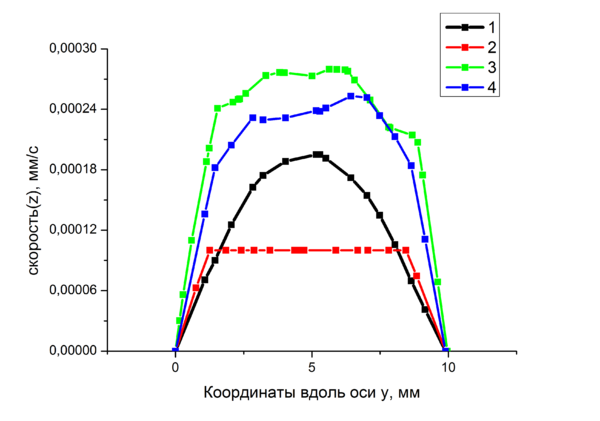
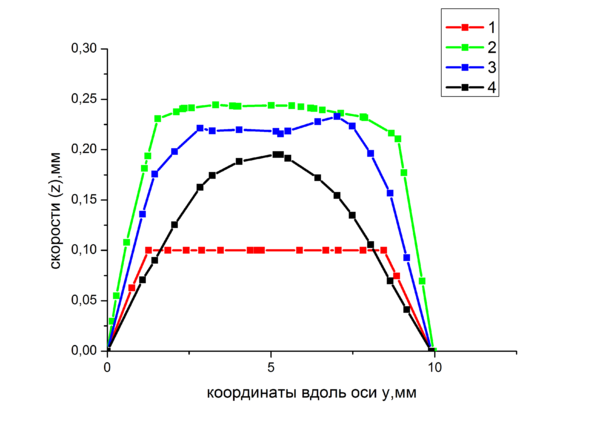
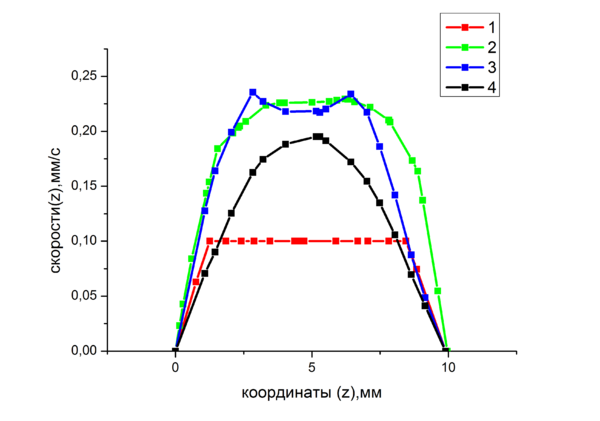
Добавление частиц привело к увеличению скорости потока предположительно из-за уменьшения общей вязкости потока.Построены профили распределения скоростей жидкости и смеси.
Так же на представленных видео ,что распределение скоростей частиц по сечению соответствует распределению скоростей жидкости.
- график показателей скорости с частицами
- график показателей давления с частицами
меняем радиусы частиц
radius 0.0003
- график показателей скоростей 1-начало ;2-середина;3-конец;4-без частиц
- график показателей скоростей 1-начало ;2-середина;3-конец;4-без частиц. 1000 итераций
- график показателей скоростей 1-начало ;2-середина;3-конец;4-без частиц. 2000 итераций