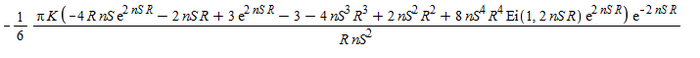Устойчивость протопланетного облака системы "Земля - Луна" часть 3

Постановка задачи

Пусть имеется тело радиуса [math]R[/math] (площадь поверхности [math]4S_1=4\pi R^2[/math])с поверхности которого отделяются частицы. На расстоянии [math]r[/math] от первого тела находится сферическое тело площадью [math]2 S_2[/math].

Требуется подсчитать силу, с которой это тело взаимодействует с частицей.

Исходим из следующих соображений.

• Все частицы имеют одинаковую массу [math]m[/math]

• Все частицы отделяются от сферического тела

1) В радиальных направлениях

2) С одинаковой начальной скоростью [math]V_0[/math]

3) без ускорения

Решение

Запишем уравнение непрерывности для среды с источником излучения.

[math](1):\frac{\partial w}{\partial t}+\bigtriangledown \cdot (w \vec V_0)=4\pi R^2 I \delta^3(r)[/math],

где

[math]w[/math]-концентрация частиц,

[math]I[/math]-Интенсивность испарения сферы [math]\frac{partical}{sek \cdot sm^2}[/math]

[math]\delta^3(r)[/math]-дельта функция Дирака.

Первое слагаемое в силу стационарности-ноль.

[math](2):w V_0 \cdot 4\pi r^2=4\pi R^2 I[/math]

[math](3):w=\frac{R^2 I}{r^2 V_0}[/math]

Рассмотрим частичку площадью [math]4\pi a^2[/math], ( площадь поперечного сечения, именно она является характеристикой взаимодействия, [math]S_2=\pi a^2[/math]) находящеюся на расстоянии [math]r[/math], от излучающего тела. Тогда переданный импульс при абсолютно-упругом ударе за время [math]\Delta t[/math] будет

[math](4):\Delta p=\frac{2 m \Delta t V_0 2\pi a^2 R^2 I}{r^2}[/math],

отсюда

[math](5):F=\frac{\Delta p}{\Delta t}=4\pi m V_0 I\frac{a^2 R^2 }{r^2}=\frac{m V_0 I}{4\pi}\frac{S_1 S_2 }{r^2}[/math]

Постановка задачи

В условиях прошлой задачи, учесть эффект экранирования.

Решение

Если среда, где распространяется излучение, не пустая, присутствует экранирующий эффект, тогда , в соответствии с [работой], концентрация отделившихся частиц на расстоянии [math]r[/math] запишется как

[math](6):w=\frac{R^2 I}{r^2 V_0} exp(-n S r ) [/math], где

[math]n=n(r)[/math] -концентрация экранирующих тел.

[math]S[/math] -площадь поперечного сечения экранирующих тел (в случае сферических тел, полагая их площадь есть [math]4S[/math]).

[math](7):F=\frac{\Delta p}{\Delta t}= \frac{m V_0 I}{4\pi}\frac{S_1 S_2 }{r^2}exp(-\rho S r )=K\frac{ S_1 S_2 }{r^2}exp(-\rho S r )[/math]

Постановка задачи

Для испаряющейся с интенсивностью [math]I[/math] сферической частицы площадью [math]4S_1[/math], в среде с частицами с концентрацией [math]w[/math] и площадью [math]4S[/math] написать выражение для созданного ей отталкивающего потенциала на расстоянии r.

Решение Характеристикой испарения, при одинаковой интенсивности является площадь частицы. Использую метод пробной сферической частицы,площадью поверхности [math]2 S_2[/math] внесенной в отталкивающее поле (тогда на наблюдателя будет обращена поверхность [math]S_2[/math] ), получим связь силы и потенциала:

[math]\varphi=-\int \frac{F}{4 S_2} dr=K S_1 \rho S \left(\frac{exp(-n S r)}{n S r}-Ei(1,n S r)\right)[/math]

[math](8:)\varphi=K S_1\left( \frac{exp(-n S r)}{r}-n S \cdot Ei(1,n S r)\right)[/math]

Постановка задачи

Для однородного шара с концентрацией частиц [math]n [/math] найти закон функцию потенциала.

Решение По антологии с гравитационным потенциалом можно показать, что на внутреннею точку полый шар не действует.

Потенциал на поверхности шара

Представим себе, что точка [math]P[/math] находится на поверхности шара. Соединим эту точку с центром шара (точка О), полученный радиус-вектор обозначим через [math]r[/math] . Радиус-вектор элемента объёма [math]dV[/math] будем обозначать буквой [math]r'[/math] . Следовательно расстояние между элементом объёма и точкой [math]P[/math] , которое мы обозначили греческой буквой [math]\rho[/math], будет иметь вид [math]\rho=\sqrt{r'^2+r^2-2rr'cos\phi}[/math] , где [math]\phi[/math]-- угол с вершиной в центре шара, образованный радиус-векторами [math]r[/math], . Наконец, объем элементарно малого параллелепипеда со сторонами [math]dr'[/math], [math]r'd\phi[/math], и [math]r'sin\phi dA[/math] . Здесь мы введена еще одна степень свободы -- поворот вокруг оси OP на угол [math]dA[/math].

Для бесконечно-малого объёма надо ввести эквиваленту площадь поверхности, равной суммарной площади всех находящихся в нём частиц.

[math]dN=ndV[/math]

[math]dS_{ekv}=dN\cdot S=ndVS[/math]

Теперь следует проинтегрировать по всем объёмам, чтобы найти суммарный потенциал.

[math](9):\varphi(r)=K \int_0^R dr'\int_0^{\pi} d\phi\int_0^{2\pi}dA \left(\frac{exp(-ns\rho)}{\rho} - n S Ei(1,nS\rho)\right)nS r'^2sin\phi [/math]

Заменим переменную интегрирования [math]\phi[/math] на [math]\rho[/math]. Определим пределы интегрирования. Очевидно, что вместо 0 и [math]\pi[/math] нужно взять [math]К-r'[/math] и [math]К+r'[/math], а [math]\rho d\rho=Rr'sin\phi d\phi[/math].

Имеем:

[math](10):\varphi(r)=2\pi K n S\int_0^R dr' \int_{R-r'}^{R+r'}d\rho\left(\frac{exp(-ns\rho)}{R} r' - n S \frac{\rho r'}{R} Ei(1,nS\rho)\right)[/math]

После интегрирования, получим

[math](11):[/math]

Потенциал во внутренней точке шара

Сила, вызванная рассматриваемым потенциалом, равна

[math]F=\frac{d\varphi(r)}{dr}[/math]

Так как внешние слои никак не действуют на помещённую во внутрь шара материальную точку, то потенциал внутри шара нужно посчитать, как

[math]\V(r)=\int \frac{d\varphi(r)}{dr} dr=\Phi(r)+C[/math], где [math]C[/math] константа интегрирования. [math]C[/math] находится из граничного условия [math]V(r)=\varphi(R)[/math], где в правую часть нужно подставить выражение из [math](11)[/math]

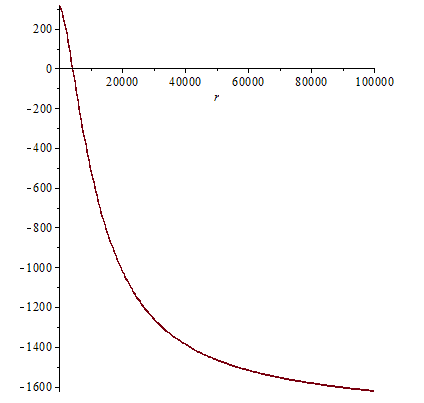
Форма получившейся кривой на рисунке ниже

Выбранные параметры [math]K=10^{-2}[/math]

[math]n\cdot S=10^{-4}[/math]

[math]R=10^{5}[/math]

Цифры

Объём и площадь сферы связаны соотношением [math]V=\frac{2}{3\sqrt{4\pi}}S^{3/2}[/math], масса ледяных пылинок

поэтому [math]m= 0.917 \cdot \frac{2}{3\sqrt{4\pi}}S^{3/2} \approx 0.17 S^{3/2} [/math]

Если теперь положить, что радиус системы Земля-Луна на начальных этапах своей эволюции был в 2 раза больше расстояния между Луной и Землёй сегодня ([math]R=7*10^10 Sm[/math]), а масса была равна суммы масс Земли и Луны, то получим [math]n=\frac{M}{Vm}=\frac{6.04\cdot 10^{27}}{2.37\cdot10^{32}\cdot 0.17 S^{3/2}}\frac{1}{sm^3}[/math]

Если половина площади частиц примерно ровна [math]600 sm^2[/math], что соответствует радиусу 10 см, то получим

[math]n=8.25\cdot 10^{-10}\frac{1}{sm^3}[/math], что примерно соответствует 1 частице в кубе 10х10 метров.

Некоторые уравнения

Для простоты рассматриваем бесстолкновительные системы

Функция распределения должна удовлетворять кинетическому уравнению Больцмана

[math] \frac{\partial f}{\partial t} + \mathbf{v}\cdot \frac{\partial f}{\partial \mathbf{r}} + \mathbf{F}\cdot m\cdot \frac{\partial f}{\partial \mathbf{v}} = \left. \frac{\partial f}{\partial t} \right|_{\mathrm{coll}} [/math]

Здесь F(r, t) — поле сил, действующее на частицы в жидкости или газе, а m — масса частиц. Слагаемое в правой части уравнения добавлено для учёта столкновений между частицами и называется интеграл столкновений. Если оно равно нулю, то частицы не сталкиваются вовсе.

Поэтому

[math] \mathbf{v}\cdot \frac{\partial f}{\partial \mathbf{r}} + \mathbf{F}\cdot m\cdot \frac{\partial f}{\partial \mathbf{v}} = 0 [/math]