Subject
Specification of double pendulum oscillations
Task
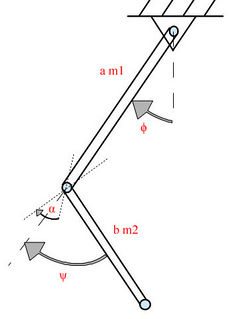
Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of the first rod via cylindrical joint so that when both rods are vertical the angle between joint's axis equals to [math]\alpha[/math]. Dissipative forces are not taken to account.
System parameters:
- Inertia tensor of first and second rods are equal. [math]\underline{\underline{\Theta}}_1[/math] and [math]\underline{\underline{\Theta}}_2[/math] respectively.
- length of rods are a and b, their masses [math]m_1[/math] and [math]m_2[/math] for first and second rods.
- Angle between rotation axis of joints equals to [math]\alpha[/math]
- [math]\varphi[/math] - angle between first rod and vertical direction
- [math]\psi[/math] - angle between axis of first and second rods that means the angle in second joint relative to vertical orientation of system.
Main task:
- find the equation of motion for this double pendulum
Solution
Let's find the way of solving this problem: We are going to solve the problem by using the Lagrange equation:
[math]\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i[/math]
- [math]T[/math] - Kinetic energy of system
- [math]\Pi[/math] - Potential energy of system
- [math]q_i[/math] - Generalized coordinates
- [math]\dot{q}_i[/math] - generalized velocities
- [math]Q_i[/math] - generalized non-potential forces
Selecting generalized coordinates: for generalized coordinates we are going to use angles [math]\varphi[/math] and [math]\psi[/math]
- In this problem we neglect non-potential interactions, so generalized non-potential forces equals to zero.
Calculating potential and kinetic energy of system: [math]\Pi_1 , T_1 ; \Pi_2 , T_2 [/math] of first and second rods relatively.
[math]\Pi = \Pi_1 + \Pi_2[/math] - Potential energy of system
[math]T = T_1 + T_2[/math] - Kinetic energy of system
[math]T_1 = \frac{\underline{\omega}_1 \cdot \underline{\underline{\Theta}}_1 \cdot \underline{\omega}_1}{2} = \frac{\Theta_1 \omega_1^2}{2} = \frac{\Theta_1 \dot{\varphi}^2}{2}[/math] - Kinetic energy of first rod; Where
[math]\qquad \Theta_1 = \frac{m_1 a^2}{3}[/math] - Inertia torque of first rod
[math]\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)[/math] - Potential energy of first rod
[math]T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}[/math] - Kinetic energy of second rod
[math]\underline{\omega}_2 = ?[/math]
Finding second rod's angular velocity vector:
For calculating [math]\underline{\omega}_2[/math] we will find rotation tensors of both rods
[math]\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)[/math]
[math]\underline{\underline{P}}_2(\psi,\underline{e}) = \underline{e}\underline{e} + (\underline{\underline{E}} - \underline{e}\underline{e})cos(\psi) + \underline{e} \times \underline{\underline{E}}sin(\psi)[/math]
Where:
[math]\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0[/math] - second rod's ongoing rotation axis
[math]\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i}[/math] - second rod's initial rotation axis
[math]\underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1[/math] - full rotation tensor for second rod
But:
[math] \underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}(\psi,\underline{e}) \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})\cdot \underline{\underline{P}}^T_1 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})[/math]
Now using the angular velocity addition formula we get:
[math]\underline{\omega}_2 = \underline{\omega}_1 + \underline{\underline{P}}_1 \cdot \underline{\tilde{\omega}}_2; \qquad \underline{\tilde{\omega}}_2 = \dot{\psi}\underline{e_0}[/math]
So we got the equation:
[math]\underline{\omega}_2 = \dot{\varphi} \underline{k} + \dot{\psi}\underline{e}[/math]
Finding second rod's center of mass velocity
[math]\underline{\vartheta}_c = \frac{1}{2}\underline{\omega}_2 \times \underline{b} + \dot{\varphi}\underline{k}\times \underline{a} ; \qquad \underline{a} = \underline{\underline{P}}_1 \cdot a\underline{j} ; \qquad \underline{b} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot b\underline{j}[/math]
Finding second rod's kinetic energy
Second rod's inertia tensor:
[math]\underline{\underline{\Theta}}_2 = \frac{ml^2}{12}\left(\underline{\underline{E}} - \underline{\tilde{e}\tilde{e}} \right) ;\qquad \underline{\tilde{e}} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot \underline{j}[/math]
Now we found all expressions required for second rod's kinetic energy formula:
[math]T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}[/math]
Finding second rod's potential energy
[math]\Pi_2 = mg(a+b - \underline{r}_c \cdot \underline{j}); \qquad \underline{r}_c = \underline{a} + \frac{1}{2}\underline{b}[/math] - radius-vector of second rod's center of mass
Finding the motion equation
We need to differentiate the equations for potential and kinetic energy, the way Lagrange equation requires and use the result in it. As the result we going to get the system of two differential equations which itself is equation of motion.
We notice that using this method we can get the motion equation also for big angles, it can be linearized assuming that angles [math]\varphi,\psi[/math] are small and dropping terms of second order.
Применение метода решения для частного случая
Проверим описанный выше метод в частном случае при [math]\alpha = 0[/math]
В таком случае задача сводится к двухмерной.
Найдем тензоры поворота
[math]\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)[/math]
[math]\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i} = \underline{k}[/math]
[math]\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0 = \underline{k}[/math]
[math]\underline{\underline{P}}_2(\psi,\underline{e})= \underline{\underline{P}}_2(\psi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\psi) + \underline{k} \times \underline{\underline{E}}sin(\psi)[/math]
Найдем угловую скорость второго стержня
[math]\underline{\omega}_2 = (\dot{\varphi}+\dot{\psi})\underline{k}[/math]
Найдем скорость центра масс
[math]\upsilon^2_c = \frac{1}{4} b^2 (\dot{\varphi}+\dot{\psi})^2 + ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + a^2\dot{\varphi}^2[/math]
Найдем кинетическую энергию второго стержня
[math]T_2 = \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)[/math]
Найдем потенциальную энергию второго стержня
[math]\Pi_2 = m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right][/math]
Найдем кинетическую и потенциальную энергии первого стержня
[math]T_1 = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2[/math]
[math]\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)[/math]
Получение уравнения движения для частного случая
Запишем выражения для полной кинетической и потенциальной энергий:
[math]T = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2 + \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)[/math]
[math]\Pi = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right) + m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right][/math]
Теперь продифференцируем энергии и произведем линеаризацию полученного результата предполагая что [math]\varphi , \psi[/math] малые углы оставив только бесконечно малые первого порядка. В результате получим уравнение движения:
[math]
\begin{cases}
\ddot{\varphi} \left( \frac{m_1 a^2}{3} + \frac{m_2 b^2}{3} + m_2 a (a+b) \right) + \ddot{\psi} \left( \frac{m_2 b^2}{3} + \frac{m_2 ab}{2} \right) + \varphi \frac{g}{2} \left((m_1+2m_2)a+m_2 b \right)+\psi \frac{g}{2}m_2 b = 0\\
\ddot{\varphi} \left( \frac{m_2 b^2}{3} + \frac{m_2 ab}{2} \right) + \ddot{\psi} \frac{m_2 b^2}{3} + \varphi \frac{g}{2} m_2 b + \psi \frac{g}{2} m_2 b = 0\\
\end{cases}
[/math]
Обсуждение результатов и выводы
В данной работе был подробно описан алгоритм решения задачи о двойном маятнике в случае когда оба шарнира циллиндрические. Затем данный метод был применен для частного случая плоской задачи.
Ссылки по теме
См. также