Dzenushko Dainis. Course project for theoretical mechanics "Double pendulum"

Subject

Specification of double pendulum oscillations

Task

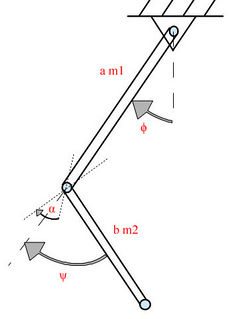
Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of the first rod via cylindrical joint so that when both rods are vertical the angle between joint's axis equals to [math]\alpha[/math]. Dissipative forces are not taken to account.
System parameters:

1. Тензоры инерции первого и второго стержней равны [math]\underline{\underline{\Theta}}_1[/math] и [math]\underline{\underline{\Theta}}_2[/math] соответственно.
2. Длины стержней равны a и b, их массы [math]m_1[/math] и [math]m_2[/math] соответственно первому и второму стержням.
3. Угол между осями вращения шарниров равен [math]\alpha[/math]
   

• [math]\varphi[/math] - угол между первым стержнем и вертикалью
• [math]\psi[/math] - угол между осью первого стержня и вторым стержнем т.е. угол во втором шарнире относительно вытянутого положения

• 



Задача:

• Найти уравнение движения системы

Решение

Определимся с подходом к решению: Задачу будем решать при помощи уравнения Лагранжа имеющего следующий вид:
[math]\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i[/math]

• [math]T[/math] - Кинетическая энергия системы
  
• [math]\Pi[/math] - Потенциальная энергия системы
  
• [math]q_i[/math] - Обобщенные координаты
  
• [math]\dot{q}_i[/math] - Обобщенные скорости
  
• [math]Q_i[/math] - Обобщенные непотенциальные силы
  

Выберем обобщенные координаты: в качестве обобщенных координат возьмем углы [math]\varphi[/math] и [math]\psi[/math]

• В нашем случае отсутствуют обощенные силы, соответствующие непотенциальным взаимодействиям.
  

Найдем потенциальную и кинетическую энергии системы: [math]\Pi_1 , T_1 ; \Pi_2 , T_2 [/math] соответственно первого и второго стержней.
[math]\Pi = \Pi_1 + \Pi_2[/math] - Потенциальная энергия системы
[math]T = T_1 + T_2[/math] - Кинетическая энергия системы
[math]T_1 = \frac{\underline{\omega}_1 \cdot \underline{\underline{\Theta}}_1 \cdot \underline{\omega}_1}{2} = \frac{\Theta_1 \omega_1^2}{2} = \frac{\Theta_1 \dot{\varphi}^2}{2}[/math] - Кинетическая энергия первого стержня; Где [math]\qquad \Theta_1 = \frac{m_1 a^2}{3}[/math] - момент инерции первого стержня
[math]\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)[/math] - Потенциальная энергия первого стержня
[math]T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}[/math] - Кинетическая энергия второго стержня
[math]\underline{\omega}_2 = ?[/math]

Найдем вектор угловой скорости второго стержня:
Для нахождения [math]\underline{\omega}_2[/math] найдем тензоры поворота первого и второго стержней
[math]\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)[/math]
[math]\underline{\underline{P}}_2(\psi,\underline{e}) = \underline{e}\underline{e} + (\underline{\underline{E}} - \underline{e}\underline{e})cos(\psi) + \underline{e} \times \underline{\underline{E}}sin(\psi)[/math]
Где:
[math]\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0[/math] - ось вращения второго стержня в данном положении
[math]\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i}[/math] - ось вращения второго стержня в начальном положении

[math]\underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1[/math] - полный тензор поворота второго стержня

Но:
[math] \underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}(\psi,\underline{e}) \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})\cdot \underline{\underline{P}}^T_1 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})[/math]

Теперь применяя формулу сложения угловых скоростей получим:
[math]\underline{\omega}_2 = \underline{\omega}_1 + \underline{\underline{P}}_1 \cdot \underline{\tilde{\omega}}_2; \qquad \underline{\tilde{\omega}}_2 = \dot{\psi}\underline{e_0}[/math]

Таким образом получаем что:
[math]\underline{\omega}_2 = \dot{\varphi} \underline{k} + \dot{\psi}\underline{e}[/math]

Найдем скорость центра масс второго стержня
[math]\underline{\vartheta}_c = \frac{1}{2}\underline{\omega}_2 \times \underline{b} + \dot{\varphi}\underline{k}\times \underline{a} ; \qquad \underline{a} = \underline{\underline{P}}_1 \cdot a\underline{j} ; \qquad \underline{b} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot b\underline{j}[/math]

Найдем кинетическую энергию второго стержня
Запишем тензор инерции второго стержня:
[math]\underline{\underline{\Theta}}_2 = \frac{ml^2}{12}\left(\underline{\underline{E}} - \underline{\tilde{e}\tilde{e}} \right) ;\qquad \underline{\tilde{e}} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot \underline{j}[/math]

Теперь мы нашли все необходимое для подставления в формулу для кинетической энергии второго стержня:
[math]T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}[/math]

Найдем потенциальную энергию второго стержня
[math]\Pi_2 = mg(a+b - \underline{r}_c \cdot \underline{j}); \qquad \underline{r}_c = \underline{a} + \frac{1}{2}\underline{b}[/math] - радиус-вектор центра масс второго стержня

Получение уравнения движения
Продифференцируем полученные выражения для потенциальной и кинетической энергий, как это требует уравнение Лагранжа и подставим полученное в него. В результате получим систему из двух дифференциальных уравнений которые описывают движение системы.
Заметим что данный метод решения дает нам уравнение движения для больших углов, в случае необходимости его можно линеаризовать предположив что углы [math]\varphi,\psi[/math] малы и отбросив слагаемые второго порядка.

Применение метода решения для частного случая

Проверим описанный выше метод в частном случае при [math]\alpha = 0[/math]
В таком случае задача сводится к двухмерной.
Найдем тензоры поворота
[math]\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)[/math]

[math]\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i} = \underline{k}[/math]
[math]\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0 = \underline{k}[/math]
[math]\underline{\underline{P}}_2(\psi,\underline{e})= \underline{\underline{P}}_2(\psi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\psi) + \underline{k} \times \underline{\underline{E}}sin(\psi)[/math]

Найдем угловую скорость второго стержня
[math]\underline{\omega}_2 = (\dot{\varphi}+\dot{\psi})\underline{k}[/math]

Найдем скорость центра масс
[math]\upsilon^2_c = \frac{1}{4} b^2 (\dot{\varphi}+\dot{\psi})^2 + ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + a^2\dot{\varphi}^2[/math]

Найдем кинетическую энергию второго стержня
[math]T_2 = \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)[/math]

Найдем потенциальную энергию второго стержня
[math]\Pi_2 = m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right][/math]

Найдем кинетическую и потенциальную энергии первого стержня
[math]T_1 = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2[/math]
[math]\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)[/math]

Получение уравнения движения для частного случая
Запишем выражения для полной кинетической и потенциальной энергий:
[math]T = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2 + \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)[/math]
[math]\Pi = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right) + m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right][/math]
Теперь продифференцируем энергии и произведем линеаризацию полученного результата предполагая что [math]\varphi , \psi[/math] малые углы оставив только бесконечно малые первого порядка. В результате получим уравнение движения:
[math] \begin{cases} \ddot{\varphi} \left( \frac{m_1 a^2}{3} + \frac{m_2 b^2}{3} + m_2 a (a+b) \right) + \ddot{\psi} \left( \frac{m_2 b^2}{3} + \frac{m_2 ab}{2} \right) + \varphi \frac{g}{2} \left((m_1+2m_2)a+m_2 b \right)+\psi \frac{g}{2}m_2 b = 0\\ \ddot{\varphi} \left( \frac{m_2 b^2}{3} + \frac{m_2 ab}{2} \right) + \ddot{\psi} \frac{m_2 b^2}{3} + \varphi \frac{g}{2} m_2 b + \psi \frac{g}{2} m_2 b = 0\\ \end{cases} [/math]

Обсуждение результатов и выводы

В данной работе был подробно описан алгоритм решения задачи о двойном маятнике в случае когда оба шарнира циллиндрические. Затем данный метод был применен для частного случая плоской задачи.

Ссылки по теме

• Double pendulum 2D Wiki
  
• Двумерный случай двойного маятника

См. также

• Справочная информация
• Список курсовых проектов
• Кафедра "Теоретическая механика"
• Дзенушко Дайнис