Учет нелинейных эффектов при описании динамических процессов в полимерах

Учет нелинейных эффектов при описании динамических процессов в полимерах - Первая часть магистерской работы: Разработка аналитических и компьютерных моделей для описания динамических процессов в полимерах и агломератах частиц Витохина Евгения проводимая под руководством Е.А. Ивановой.

Цель работы

В ряде работ предложена линейная теория термовязкоупругости, включающая уравнения теплопроводности гиперболического типа. Цель данной работы заключается в распространении этой теории на два случая нелинейности. Первый случай: учет нелинейной зависимости напряжений от механических деформаций. Второй случай: учет нелинейных тепловых эффектов.

Эксперимент

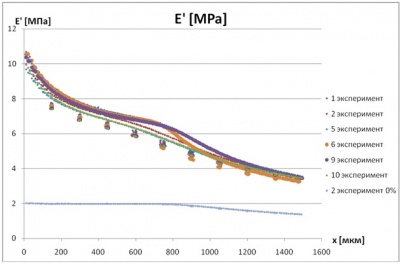
Учет нелинейности базируется на результатах экспериментальных исследований, проведенных в рамках научной работы на кафедре МСС и ВТ Пермского Государственного Университета. В ходе экспериментальной работы были получены зависимости динамического модуля упругости, модуля потерь и сдвига фаз от амплитуды перемещений в одной серии опытов, и от температуры в другой серии опытов. Выявлен нелинейный характер полученных зависимостей.

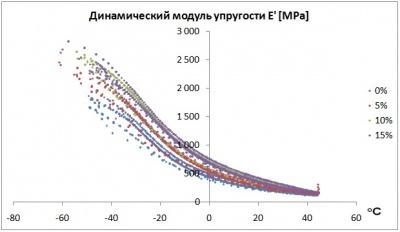
Динамический модуль упругости полиэтилена с различным процентом содержания глинистого нанонаполнителя в зависимости от температуры для частоты 0,1 Гц

Динамический модуль упругости чистой резины и с 40% содержанием сажи при частоте 1Гц в зависимости от амплитуды перемещений

Аналитические зависимости

Выражая параметры теории термовязкоупругости, предложенной Ивановой Е.А., через экспериментальные данные, было получено следующее выражение для объемной вязкости:

[math]\eta_v=\frac{\lambda}{c_v}-\frac{1}{\omega}\left(\frac{E_2}{E_1}\right)\left(\frac{1}{E}-\frac{1}{E_1}\right)^{-1}[/math]

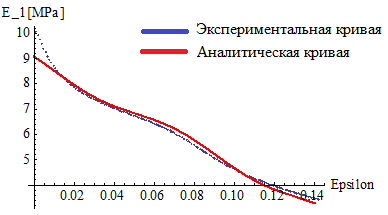
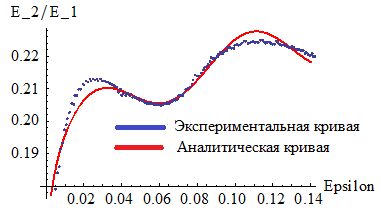
Таким образом задача свелась к аппроксимации зависимостей [math]E_1(\varepsilon)[/math] и [math]\frac{E_2}{E_1}(\varepsilon)[/math]. В итоге были получены следующие аналитические кривые:

Аналитическая кривая: [math]E_1=a_1\varepsilon+a_2\sin(\Omega_1\varepsilon-\varphi_1)+a_3[/math]

Аналитическая кривая: [math]\frac{E_2}{E_1}(\varepsilon)=b_1+b_2\ln(1+b_3\varepsilon)+b_4\sin(\Omega_2\varepsilon)[/math]

Нелинейные уравнения

В результате предложены нелинейные уравнения, описывающие поведение термовязкоупругих стержней, изготовленных из материалов типа полиэтилена, наполненного наночастицами, и углеродсодержащей резины

Численное решение линейной задачи термоупругости

Численное решение полученных нелинейных уравнений термовязкоупругости является весьма трудоемким, по этой причине сперва было проведено создание численного алгоритма и написание компьютерной программы для нахождения решения линейной задача термоупругости с целью сравнения данного решения с аналитическим. Это сравнение позволит протестировать программу и сделать вывод о правильности ее работы, для дальнейшего нахождения с ее помощью решения нелинейной задачи.