Тема проекта
Описание колебаний плавающих тел.
Постановка задачи
Найти уравнение колебаний для следующих тел:
1) Шар
2) Параллелепипед
- Вертикальные колебания
- "Бортовая качка"
Решение
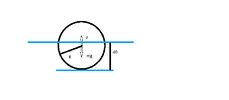
1) Шар
ПУР: [math]mg = \rho g V_0 = \frac{\pi \rho g} {3} d_0^2 (3R-d_0);[/math]
Второй закон Ньютона примет вид:
[math]m \ddot x = mg - \frac{\pi \rho g} {3} (d_0+x)^2 (3R-d_0-x)[/math]
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0+x)^2(3R-d_0-x)[/math]
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0^2 + 2 d_0x + x^2)(3R-d_0-x)[/math]
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0^2 + 2 d_0x + o(x^2))(3R-d_0-x)[/math]
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0^2 + 2 d_0x + o(x^2))(3R-d_0-x)[/math]
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(3d_o^2R - d_0^3 + 6d_0Rx - 3d_0^2x)[/math]
[math]m \ddot x = - \frac{\pi \rho g} {3}(6d_0Rx - 3d_0^2x)[/math]
[math]m \ddot x = \pi \rho g d_0(-2 R + d_0)x[/math];
Так как [math](-2 R + d_0) \lt 0[/math] формула имеет вид [math]m \ddot x + \pi \rho g d_0(2 R - d_0)x = 0[/math]
Остается проверить размерность величины [math]\frac{\pi \rho g d_0(2 R - d_0)} {m} = \frac {1} {s^2}[/math]
Уравнение колебаний найдено.
2) Вертикальные колебания параллелепипеда
ПУР: [math]mg = \rho g V_0 = mg = \rho g S d_o;[/math]
Второй закон Ньютона примет вид:
[math]m \ddot x = mg -\rho g S (d_o + x)[/math]
[math]m \ddot x = -\rho g S x[/math]
Остается проверить размерность величины [math]\frac{\rho g S} {m} = \frac {kg m^3} {s^2 m^3 kg} = \frac {1} {s^2}[/math]
Уравнение колебаний найдено.
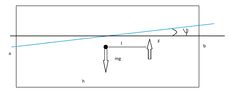
2) Бортовая качка
Очевидно, что модуль силы Архимеда остается постоянным(так как постоянным остается объем погруженной части тела в силу симметрии тела).
Меняется только точка приложения, что и создает момент силы Архимеда, вызывающий колебания. Тогда уравнения примут вид:
[math]\Theta_c \ddot \varphi = F_a l[/math]
[math]l = h \frac {h \varphi} {6 d}[/math]
Так как тело плавает [math]F_a = mg[/math]
Обсуждение результатов и выводы
1) Интересно то, что [math]\frac{\rho g S} {m} = k \frac{g} {l}[/math], где l - полная высота параллелепипеда, а k - коэффициент, равный отношению плотности тела к плотности жидкости
Ссылки по теме
Архимед
См. также