Нейронные сети - теория и приложения.

Искуственные нейронные сети

Нейронная сеть это вычислительная модель, созданная на основании исследований работы нервной системы человека как попытка создания искуственного интелекта. Разумеется это лишь упрощенная модель, которая не отражает всей сложности процессов происходящих в мозгу человека, однако она нашла применение в областях, где традиционные методы расчета не применимы.В основном это решение задач, сформулировать которые математически крайне сложно, а зачастую и невозможно. Искуственные нейронные сети применяются для:

• Распознование образов

Символов,звуков,анализ изображений. Сеть обучается набором известных образов, а затем может самостоятельно классифицировать до этого не известные ей образы.

• Управление

Создание так называемых мастер-систем, способных принимать решение подобно человеку, управлять техникой даже в случае поломок. Мастер-системы характеризуются значительной адаптивностью. Как правило на вход подаются данные о состоянии системы (Например ориентация самолета в пространстве, его скорости,параметры среды и желаемое направление полета),а на выходе сеть сообщает управление,которое необходимо применить к систем, с целью минимизации функции оценки(например расхождение текущего курса с желаемым).

• Составление прогнозов

Например на котировки акций, сеть обучается по архивам биржи,а затем строит предположение о развитии ситуации на рынке.

• Ассоциативная память

Сети способны запоминать информацию подобно человеческому мозгу, что способствует эффективному сжатию

Структура сети

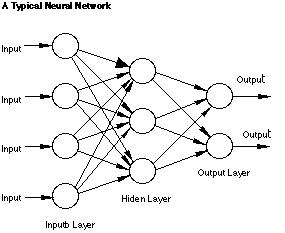
Сеть состоит из элементов называемых нейронами, соединенных связями, причем каждая связь характеризуется весом. Вес - это коэффициент на который умножается сигнал при прохождении через связь. Нейроны объединяются в слои, нейронная сеть обязательно имеет входной и выходной слои. Количество внутренних или скрытых слоев может быть произвольным, однако по мере увеличения их количества усиливается память сети, что негативно влияет на обучение. Поэтому обычно используются сети с меньшим количеством слоев, но с большим количеством нейронов в каждом.

Активация нейронов

Каждый нейрон представляет из себя некоторую функцию,ее называют функцией активации. В зависимости от предназначения сети испольуются различные типы :

• Бинарные

В зависимости от значения поступившего на вход, нейрон возвращает либо 0 либо 1. Чаще всего используется Функция Хевисайда

[math]\theta(x)=\begin{cases} 0, & x\lt 0; \\ 1, & x\geqslant 0.\end{cases}[/math]

• Линейные

[math]U(x)=\mu x[/math]

• Нелинейные

Нелинейные функции акивации позволяют добиваться результатов меньшим числом нейронов. Наиболее используемой является сигмоидная функция.

[math]U(x) = \frac{1}{1 + e^{-x}}.[/math]

Обучение

Для обучения применяется алгоритм обратного распространения ошибки. У сети есть множество входов [math]x_1, ..., x_n[/math], Обозначим через [math]w_{i,j}[/math] вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через [math]o_i[/math] — выход i-го узла. Если нам известен обучающий пример (правильные ответы сети [math]t_k[/math]), то функция ошибки, полученная по методу наименьших квадратов, выглядит так:

[math]E(\{w_{i,j}\}) =\cfrac{1}{2} \sum_{k} (t_k - o_k)^2 [/math]

На каждом шаге будем добавлять к весу.

[math]\Delta w_{i,j} = -\eta \frac {\partial E}{\partial w_{i,j}}[/math],

где [math]0 \lt \eta \lt 1[/math] -- множитель, задающий скорость "движения".

Алгоритм

При программировании алгоритм выглядит следующим образом:

1. Для всех d от 1 до m:

   1. Подать [math]\{x_i^d\}[/math] на вход сети и подсчитать выходы [math]o_i[/math] каждого узла.
   2. Для всех [math]k [/math]

      [math]\delta _k = o_k(1 - o_k)(t_k - o_k)[/math].

   3. Для каждого уровня l, начиная с предпоследнего:

      Для каждого узла j уровня l вычислить

      [math]\delta _j = o_j(1 - o_j)\sum_{k \in Children(j)} \delta _k w_{j,k}[/math].

   4. Для каждого ребра сети {i, j}

      [math]\Delta w_{i,j} = \alpha \Delta w_{i,j} + ( 1 - \alpha ) \eta \delta _j o_{i}[/math].

      [math]w_{i,j} = w_{i,j} + \Delta w_{i,j}[/math].

2. Выдать значения [math]w_{ij}[/math].

где [math]\alpha[/math] - коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции

Использование

На практике, удобнее разрабатывать алгоритмы в пакете Matlab, где для работы с нейронным сетями есть Neural Network Toolbox. Его средствами можно построить сеть и обучить ее на наборе данных. Для удобства пользователя предусмотрен GUI который запускается командой >>nnstart

Кроме того, можно использовать инструменты NNToolbox прямо в коде

Попробуем решить простейшую задачу экстраполяции на примере параболы.

Данные для обучения
inputs = [1:10];
targets =inputs.*inputs;
  
Создание сети и задание количества нейронов в скрытом слое
hiddenLayerSize = 1щ;
net = fitnet(hiddenLayerSize);
Деление данных на набор для обучения,валидации и тестирования.
net.divideParam.trainRatio = 80/100;
net.divideParam.valRatio = 20/100;
net.divideParam.testRatio = 0/100;
Обучение сети
[net,tr] = train(net,inputs,targets);
Тестирование 
outputs = net(inputs);
errors = gsubtract(targets,outputs);
performance = perform(net,targets,outputs)