Устойчивость протопланетного облака системы "Земля - Луна" часть 2

Вторая модель

(Черновые тезисы)

• Вопрос на который должна дать данная часть работы, можно сформулировать так: "Как изменится концентрация испарившихся молекул после прохождения через испаряющейся участок пылевого облака"

• Работа состояла из двух частей: Компьютерного 2D моделирования эксперимента и поиска аналитического решения.

• Эксперимент и аналитика дали хорошее совпадение результатов. Рисунки представлены ниже.

рис. 1. Прохождение "лучей" через неиспаряющееся облако.

рис. 2. Прохождение "лучей" в испаряющемся облаке.

рис. 3. Сумма двух вкладов.

рис. 4. Эта зависимость от расстояния при заданной концентрации.

Об аналитическом решении

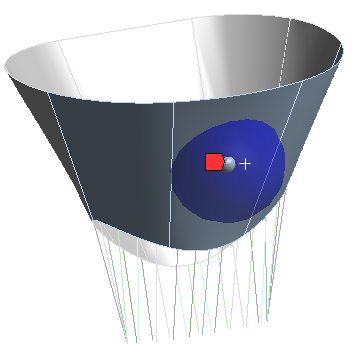
Чтобы найти закон распространения радиационного излучения в облаке, воспользуемся простой моделью. Некоторый объём пространства представим в виде цилиндра с основанием [math]H[/math] и длиной [math]L[/math]. В этом цилиндре находятся частицы-сферы радиуса r.

Пусть, перпендикулярно основанию в цилиндр, по прямым траекториям входят N лучей радиационного излучения. Рассматривается случай, когда нет никаких отражений, т.е. луч упавший на сферу, ей тотчас поглощается.

Наша задача ответить на вопрос: сколько в среднем лучей достигнет противоположной стенки цилиндра?

Эта задача равносильна следующей: На некоторой поверхности [math]H[/math] нанесена в случайном месте точка. На поверхность набрасываются случайным образом [math]N[/math] окружностей площадью [math]S[/math] [math](S=\pi r^2)[/math]. Какова вероятность того, что точка останется непокрытой? Будем решать её.

Ответ легко получить из закона распределения Пуассона.

Для начала-формальное определение:

Пусть производится [math]n[/math] независимых испытаний. Если число испытаний [math]N[/math] достаточно велико, а вероятность появления события [math]А[/math] в каждом испытании мало ([math]p\in(0,1)[/math]), то вероятность появления события [math]А[/math] [math]k[/math] раз находится следующим образом:

[math]P_n(k)=\frac{\lambda^k e^{-\lambda}}{k!}[/math]

Сделаем важное допущение – произведение [math]np[/math] сохраняет постоянное значение: [math]np=\lambda[/math] Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном [math]N[/math]) остается неизменным.

Очевидно, что вероятность того, что точка покроется одной окружностью есть отношение площади окружности к площади поверхности:[math]p=\frac{S}{H}[/math]. Тогда для [math]N[/math] окружностей эта вероятность: [math]\lambda=\frac{n\cdot S}{H}[/math]

Вероятность, что точка будет покрыта ровна [math]к[/math] окружностями из [math]n[/math] даёт формула Пуассона.

Нас интересует случай, когда [math]k=0[/math]. Случай ,когда точка не покрылась ни одной окружностью, т.е. случай, когда луч прошёл через цилиндр со сферами ни встретив ни одну на своём пути.

Подставляя [math]k=0[/math], в формулу Пуассона, находим [math]P_n(0)=e^{-\lambda}[/math].

Поэтому из [math]N[/math] лучей в среднем пройдёт

[math]N_{ex}=N\cdot e^{-\lambda}=N\cdot e^{-\frac{n\cdot S}{H}}=N\cdot exp(-n\cdot S \cdot l) [/math].......................................(1)

лучей.

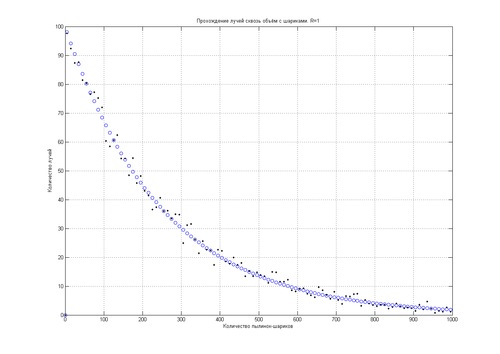
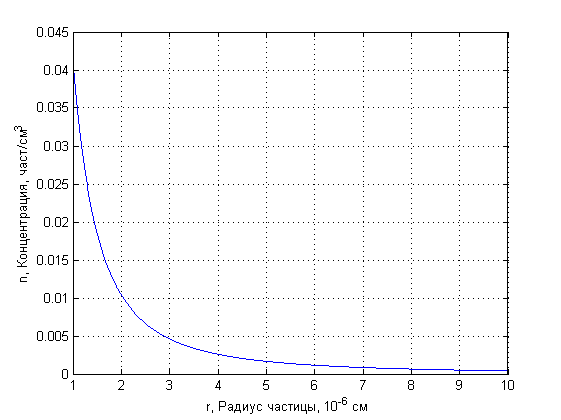
Зависимость числа пройдённых лучей от концентрации в некотором объёме проиллюстрирована на рис. 1.

Теперь рассмотрим другую ситуацию.

Тот же объём и те же шарики. Но теперь радиационное излучение не падает на стенки цилиндра, а каждый шарик излучает в произвольном направлении луч. Спрашивается, сколько лучей пройдёт через основание цилиндра?

Сперва откажемся от требования произвольности направления излучения. Пусть луч выходит из центра шарика в направлении основания [math]H[/math]. Тогда для луча с шарика, находящегося на расстоянии [math]x[/math] от поверхности [math]H[/math], вероятность прохожднения через оставшейся объём одного луча есть

[math]N_j^{*}=e^{-\frac{n\cdot S\cdot x}{H\cdot L}}[/math].................................................................(2)

где [math]L[/math] это длинна цилиндра. Соответственно, если излучается [math]I[/math] лучей, то последнее выражение надо умножить на [math]I[/math].

Чтобы найти количество лучей вышедших из бесконечно тонкого объёма, параллельного [math]H[/math], и находящегося на расстоянии [math]x[/math], очевидно необходимо (2) умножить на [math]N/L[/math].

Для всех шариков в цилиндре:

[math]N_j=\frac{N\cdot I}{L}\int_{0}^{L} e^{-\frac{n\cdot S\cdot x}{H\cdot L}} dx =\frac{N\cdot I\cdot H}{n\cdot S}(1-e^{-\frac{n\cdot S}{H}} ) [/math].................................................(3)

Для того, чтобы учесть случайность направления луча, следует выражение (3) умножить на вероятность того, что луч попадёт в угловой сегмент с основанием [math]H[/math] и вершиной в центре частички.

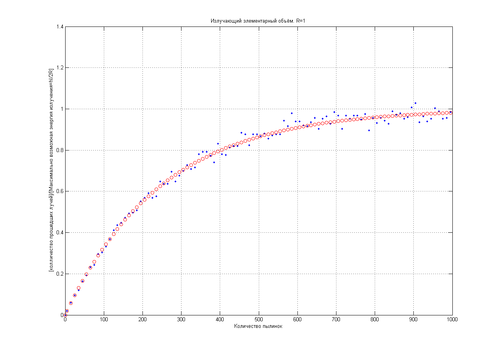
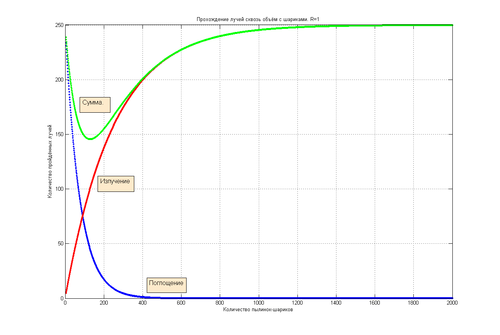
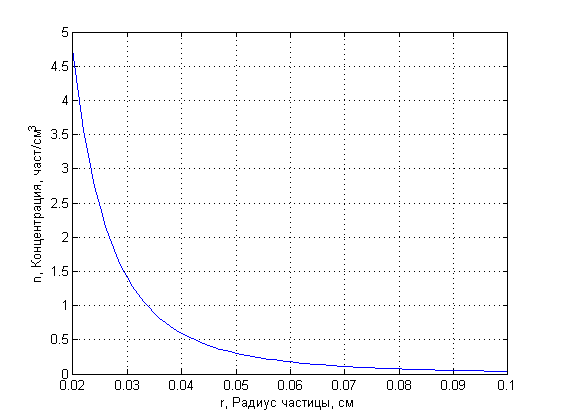
Иллюстрацию этого закона можно видеть на рис. 3.

К сожалению, это выражение столь сложно, что интеграл "руками" не берётся. Поэтому проводилось только численное интегрирование.

[math]N_j=\int_0^l I\cdot n\cdot \left(2\cdot arctg(\frac{H}{x})\cdot H- x\cdot ln(1+\frac{H^2}{x^2})\right)\cdot exp(-n \cdot S \cdot x)[/math]......................................................(4)

, где [math]n[/math]-концентрация пылинок

[math]I[/math]- интенсивность испарения.

Оценки для устойчивости

Две частицы в протопланетном облаке взаимодействуют по средством гравитации и радиационного излучения, вызванного испарением частицы.

Сила гравитационного притяжения:

[math]F_g=G\frac{m^2}{r^2}=\frac{16 \pi^2 G\rho_p^2 r_p^6}{9 r^2}[/math].......................................(5)

Сила радиационного отталкивания в пустом пространстве есть

[math]F_v=\frac{N m_0 v r_p^2}{4 r^2} [/math]

При выводе этой формулы, столкновения между молекулами не учитывалось.

Если ввести

[math]Nm_0=4\pi r_p^2 \nu[/math]- количество массы испаряющееся с пылинки за единицу времени (величина независящая от размеров частицы), то предыдущая формула перепишется, как

[math]F_v=\frac{\pi \nu v r_p^4 }{4 r^2} [/math]..................................................................(6)

[math]k=\frac{f_v}{f_g}= \frac {9\nu v}{16\pi G r_p^2 \rho^2} [/math]

При [math]k=1[/math], силы газодинамического отталкивания, полностью уравновешивают силу гравитационного притяжения (рис.5).

Для пространства заполненного другими частицами, создающими экранирующий эффект

[math]F_v=\frac{\pi \nu v r_p^4 exp(-n \cdot \pi r_p^2 \cdot r)}{r^2}[/math]..................................................................(7)

,Где [math]n[/math]-концентрация пылинок в рассматриваемом объёме.

При равенстве этих сил облако будет находиться в равновесии.

Между тем, понятно, что при любой, отличной от нуля концентрации и при любом, отличном от нуля размере пылинок будет присутствовать эффект экранирования. Взаимодействие далёких частиц будут всё более отходить от закона обратных квадратов.

Введём необходимые для дальнейшего переменные.

[math]r_p[/math]-радиус частицы,

[math]L[/math]-диаметр протопланетного облака,

[math]R[/math]-радиус конденсированного вещества всего облака.

[math]V[/math]-Объём протооблака [math], V=\frac{4}{3}\pi\frac{L^3}{2^3}[/math],

[math]N[/math]- количество частиц.

[math]m[/math]-масса частицы.

[math]M[/math]-Масса протооблака (которая равна массе конденсированного состояния всего вещества).

[math]\rho[/math]- плотность вещества частицы.

[math]V_0[/math]-объём конденсированного вещества всего облака.

На основании этого решим несколько простых задач.

Задача 1

Какими параметрами должны обладать частицы, чтобы в протопланетном облаке, размером с систему "Земля-Луна", можно было пренебречь экранированием? Какая масса будет у такой системы?

рис.5

Будем считать, что облако может находиться в равновесии, если отношение сил радиационного отталкивания и гравитационного притяжения отличается от единицы на некий малый параметр [math]k[/math].

[math]\frac{F_v}{F_g}\le k= 1-p[/math] ....................................................(8)

[math]p[/math]- число много меньшее 1.

[math]\frac{F_v}{F_g}=\frac{9\nu v \cdot exp(-n \cdot \pi r_p^2 \cdot r)}{16 \pi G r_p^2\rho^2 }[/math]

Среднею скорость примем равной среднему значению модуля скорости идеального газа:

[math]v=\sqrt{\frac{8RT}{\pi}}[/math]

Диаметр облака равен удвоенному среднему расстоянию между Землёй и Луной ( [math]L=7.68\cdot 10^{10}[/math] см ).

Пусть на расстоянии [math]2L[/math] условие (8) становится равенством.

Условие [math]\frac{F_v}{F_g}=\frac{9\nu v }{16 \pi G r_p^2\rho^2 } =1 [/math], означает, что в отсутствии экранирования облако в равновесии.

рис.6

Учёт экранирования, добавляет в произведение член [math] exp(-n \cdot \pi r_p^2 \cdot 2L)[/math]. Следовательно этот член равен [math]k[/math].

[math] n \cdot \pi r_p^2 \cdot L=-ln(k) [/math]

Выразим эту зависимость через более удобные величины:

Будем считать, что облако сферическое.

[math]S=\pi r_p^2[/math]

[math]n=\frac{N}{V}[/math],

но [math]N=\frac{(4/3)\pi R^3}{(4/3)\pi r_p^3}[/math],

Поэтому [math]n=\frac{R^3}{r_p^3} \frac{6}{\pi L^3}[/math]

Тогда [math]n \cdot S \cdot L=\pi r_p^2 \cdot \frac{R^3}{r_p^3} \frac{6}{\pi L^3} \cdot L= 6 \left( \frac{r_p}{L}\right)^2 \left( \frac{R}{r_p}\right)^3[/math]

Ответ задачи:

В протопланетном облаке, фиксированного размера можно пренебречь экранированием, если будет выполняться условие:

[math]6 \left( \frac{r_p}{L}\right)^2 \left( \frac{R}{r_p}\right)^3=-ln(k)[/math],

где [math]k[/math]- число меньшее 1.

Если принять [math]k=0.99[/math].

[math] n \cdot r_p^2=0.8\cdot 10^{-13} [/math]

Тогда построим зависимость концентрации от радиуса частицы, при условии сохранения постоянным их произведения.

Радиус порядка [math]10^{-6}[/math] см, всего в 100 раз больше характерных размеров молекул водяного пара.

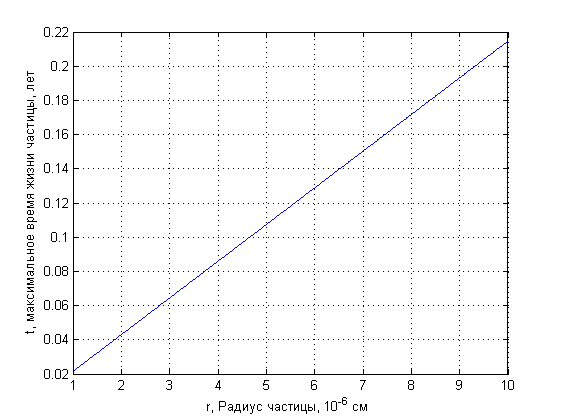
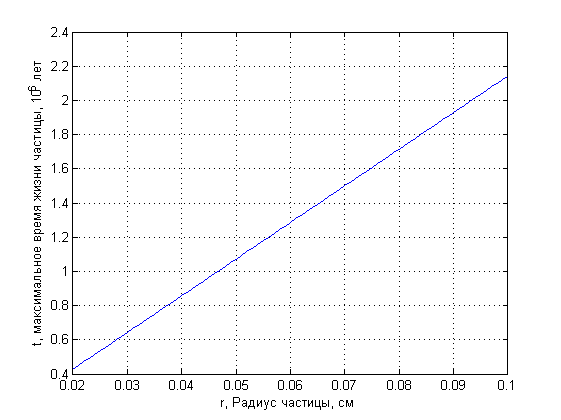
На рис. 6 приведена зависимость времени жизни частицы от радиуса. Интенсивность испарения расчитыалась из предпосылки исходного равновесия облака.

Время жизни определяется из формулы

[math]t_{max}=\frac{\rho r_p}{\nu}[/math]

На рис. 7 Масса протопланетного облака от размеров частиц. То что она растёт линейно, не удивительно. Ибо масса частиц хоть и увеличивается как куб радиуса, зато их концентрация падает, как квадрат радиуса.

рис.7

Значение Итоговой Массы в [math]10^{14}[/math] много меньше массы Земли ([math]10^{24}[/math])

Задача 2

Какие параметры будут у частиц, при фиксированных размере и массе протооблака?

Понятно, что требовать, чтобы каждая частица взаимодействовала с каждой, глупо, так как на больших расстояниях случайные флуктуации космологических факторов (давление света, плотность газа, случайные грав. сгустки.) будут оказывать на частицы большее воздействие.

Поэтому необходимо ввести радиус обрезания гравитационных сил.

Предположим помимо устойчивости облака то, что его масса порядка 1/10 массы системы Земля-Луна, то есть [math]6\cdot 10^{26}[/math] грамм.

Задача состоит в том, чтобы найти такой радиус обрезания [math]l[/math] рассматриваемых сил, чтобы выполнялось условие

[math]nSl=-ln(k)[/math]

[math]n=N/V=\frac{m}{M V}=\frac{\rho(4/3)\pi r_p^3}{M \pi L^3/6}=6\frac{\rho}{M}\cdot \left( \frac{r_p}{L}\right)^3[/math]

Поэтому

Ответ задачи:

[math]6\frac{\rho}{M}\cdot \left( \frac{r_p}{L}\right)^3 \cdot \pi r_p^2 l=\pi \left(\frac{r_p}{L}\right)^3\left(\frac{r_p}{R}\right)^2\left(\frac{l}{R}\right)=-ln(k)[/math]

Коэффециент [math]k=0.99[/math] оставим без изменения.

рис.7

рис.8

Ссылки по теме

• Снимки зарождающихся планетных систем в туманности Ориона, полученные космическим телескопом Хаббл
• А. Мурачев. Некоторые замечания по модели образования системы Земля-Луна в результате ротационного коллапса газопылевого облака (черновые наброски). Скачать презентацию, pptx: 2741 kb