Динамическая потеря устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость

Курсовой проект по Механике дискретных сред

Исполнитель: Барсуков Севастьян

Группа: 3630103/60101

Семестр: осень 2019

Постановка задачи

Исследовать динамическую потерю устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость при различных начальных отклонениях, а также при различных скоростях последней частицы.

Построение модели

В данной работе моделирование цепочки проводится методом динамики частиц.

Уравнение движения: [math] m\bar{a} = \bar{F_c} + \bar{F_s} [/math]

Метод решения

Для решения задачи использовался метод Верле (leapfrog):

[math] a_i = F(x_i), [/math]
[math] v_{i+\frac {1}{2}} = v_{i-\frac {1}{2}} + a_i dt, [/math]
[math] x_{i+1} = x_{i} + v_{i+\frac {1}{2}} dt[/math]

Начальные условия

Частицы обладают случайными начальными вертикальными смещениями:
[math]y_i = y_{rand}[/math]
[math]y_0 = 0[/math]
[math]y_n = 0[/math]

Граничные условия

Левый конец цепочки закреплен, правому задана постоянная скорость.
[math]u_0 = 0[/math]
[math]u_n = -v[/math]

Параметры системы

Для проведения моделирование задаются следующие параметры: масса частиц [math] m=10[/math], жесткость угловой пружины [math] c=10000[/math], количество частиц в цепочке [math] n=10[/math]

Взаимодействия в системе

В системе имеется два типа взаимодействия:
1. Потенциал линейной пружины:
Частицы соединены линейной пружиной:
[math]П_k= \frac {k(r)^2}{2}[/math]
где k - линейная жесткость пружины; r – расстояние между частицами.
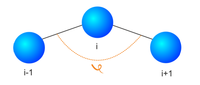
2. Потенциал угловой пружины:

Рис.1 Угловая пружинка

Частицы соединены угловой пружиной, как показано на рис. 1:
[math]П_s= \frac {c_s(φ-π)^2}{2}[/math]
где Cs – жесткость, φ – угол образованный 2-мя соседними связями.