Эффективное решение задачи гидроразрыва с использованием модифицированной постановки на примере модели ХГД

МАГИСТЕРСКАЯ РАБОТА
Автор работы: А.Д. Степанов
Научный руководитель: д. ф-м. н. профессор, А. М. Линьков

Введение и мотивация работы

Гидроразрыв пласта (ГРП) --- метод, широко применяющийся в газо- и нефтедобывающей промышленности для интенсификации добычи углеводородов из скважин.

Методика гидроразрыва заключается в следующем: сначала в скважине путем перфорирования создается ""зародыш"" трещины --- перфорация, после этого в скважину закачивается вязкая жидкость, что вызывает рост давления, который приводит к развитию трещины. Затем, когда трещина достаточно раскрывается, в нее закачивают специальный материал --- проппант, предотвращающий закрытие трещины.

Одна из особенностей проведения ГРП состоит в трудности контроля за происходящими на большой глубине процессами. Проведение экспериментов для исследования ГРП так же затруднено в силу сложности интерпретации получаемых данных. Поэтому для лучшего понимания и контроля ГРП необходимы и широко применяются численные модели.

В ряде работ были показаны трудности, возникающие при решении задачи о гидроразрыве в ее традиционной формулировке, связанные с сильной нелинейностью входящих в нее операторов, с необходимостью использовать нелокальный гиперсингулярный оператор для описания упруго отклика породы, сингулярностью давления у вершины трещины, возникающей при пренебрежении отставанием фронта жидкости от кончика трещины, и наличием подвижной границы. Эти трудности оказывают существенное влияние на скорость и качество работы симуляторов.

Для эффективного решения задачи о гидроразрыве была разработана модифицированная постановка, заключающаяся в выборе удобных переменных (скорость частиц жидкости и раскрытие трещины), использовании уравнения скорости вместо уравнения глобального баланса массы и применении универсального асимптотического зонтика.

Не преодолевая до конца упомянутые трудности, связанные с нелинейностью задачи, сингулярностью давления у вершины трещины и необходимостью использовать гиперсингулярный оператор, модифицированная постановка дает возможность использовать эффективные численные методы отслеживания фронта.

На данный момент преимущества модифицированной постановки были показаны на 1D задачах. Получены новые аналитические и точные численные решения. В этих работах применялись упрощения, доступные только в 1D случае:

• нормировка координаты на длину трещины;
• вместо гиперсингулярного оператора, использовался обратный ему (слабо сингулярный оператор).

Для применения модифицированной постановки к 3D задаче полезно заново решить 1D задачи, не используя доступных в частном случае упрощений.

Цели исследования

Численное решение задачи ХГД с использованием модифицированной постановки с учетом того, что

• решение находится в глобальных координатах;
• для описания упругого поведения породы используется гиперсингулярный интеграл.

Исследование возможности ускорения вычислений.

Модифицированная постановка задачи ХГД

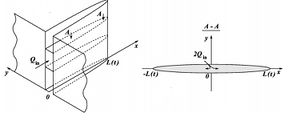
Решается задача ХГД, геометрия которой приведена на рисунке. Для практически важного случая следует рассматривать жидкость со степенным реологическим законом:

[math]\tau =M\dot{\gamma}^{n}[/math]

где [math] \tau [/math] - сдвиговые напряжения, [math] \dot{\gamma} [/math] - скорость сдвига, [math] M [/math] - индекс консистенции, [math] n [/math] - индекс поведения жидкости. Для ньютоновской жидкости [math] n = 1 [/math]; для идеально пластической [math] n= 0[/math]. На практике обычно используют утончающуюся жидкость [math] 0 \lt n \lt 1 [/math].

В согласии с модифицированной постановкой уравнения неразрывности и Пуазейля записываются, соответственно, в виде:

[math]\frac{\partial w}{\partial t}=-\frac{\partial \left( wv\right) }{\partial x} -q_{l},[/math]

[math]v=\left[ \frac{w^{n+1}}{\mu ^{\prime }}\left( -\frac{\partial p}{\partial x}% \right) \right] ^{1/n}, \label{eq::poiseuille_eq} [/math]

где [math] w [/math] - раскрытие трещины, [math] p [/math] --- давление в трещине, [math] q_l [/math] --- утечки жидкости в пласт, [math]\mu ^{\prime }=\theta M[/math], [math]\theta =2\left[ \frac{2(2n+1)}{n}\right] ^{1/n}[/math].

Как обычно, можно пренебречь отставанием фронта жидкости от фронта трещины. Тогда уравнение скорости принимает вид:

[math]\frac{dx_{\ast }}{dt}=v_{\ast }=\lim_{x\rightarrow x_{\ast }}\left( -\frac{ w^{n+1}}{\mu ^{\prime}}\frac{\partial p}{\partial x}\right) ^{1/n}.[/math]

Для нахождения раскрытия трещины необходимо воспользоваться гиперсингулярным интегралом теории упругости, который в рассматриваемом частном случае принимает вид:

[math]p(x,t)=-\frac{E^{\prime }}{4\pi }\int_{0}^{x_{\ast }}\left[ \frac{1}{\left( \xi -x\right) ^{2}}+\frac{1}{\left( \xi +x\right) ^{2}}\right] w(\xi ,t)d\xi ,\qquad \qquad 0\leq x\leq x_{\ast }, [/math]

где [math]E^{\prime }=\frac{E}{1-\nu ^{2}}[/math], [math] E [/math] --- модуль [math] \nu [/math] --- коэффициент Пуассона. При записи уравнения было учтено, что задача симметрична относительно начала координат ([math]w(-x)=w(x)[/math], [math]p(x)=p(-x)[/math]). Предполагается, что раскрытие трещины принадлежит классу функций, для которого верно

[math]w(x_{\ast },t)=0. \label{eq:boundary_condition_right}[/math]

Рост трещины описывается в рамках линейной механики разрушения. Критерием распространения трещины служит достижение КИН критического значения:

[math]K_{I}=K_{IC}.[/math]

Это уравнение можно переписать в следующем виде:

[math]w(x,t)=\sqrt{\frac{32}{\pi }}\frac{K_{IC}}{E^{\prime }}\sqrt{x_{\ast }-x} +O\left( (x_{\ast }-x)^{\alpha }\right) , \label{eq:opening_near_tip} [/math]

где [math]1\geq \alpha \gt 1/2[/math]. Рассмотрим важный для практики случай, когда основное сопротивление продвижению трещины вызвано вязкостью жидкости [math] \mu ^{\prime } [/math], а не трещиностойкостью [math] K_{IC} [/math]. Тогда можно считать, [math] K_{IC} =0[/math]. В таком случае универсальный асимптотический зонтик принимает вид:

[math]w=t_n^{1-\alpha}A_{\mu }(\alpha )v_{\ast }^{1-\alpha } \left( x_{\ast }-x\right)^{\alpha },[/math]

где [math]\alpha =2/(n+2)[/math], [math]A_{\mu }(\alpha )=\left[ \left( 1-\alpha \right) B(\alpha )\right] ^{-\frac{\alpha }{2}}[/math], [math]B(\alpha )=\frac{\alpha }{4}\cot [\pi (1-\alpha )][/math], [math] t_n = \left(\frac{\mu^\prime}{E^\prime}\right)^\frac{1}{n} [/math].

Подставляя УАЗ в уравнение скорости, получаем:

[math]\frac{dx_{\ast }}{dt}=v_{\ast }=\frac{1}{t_n} [A_{\mu }(\alpha )]^{-\frac{1}{1-\alpha } }\lim_{x\rightarrow x_{\ast }}\left[ \frac{w(x)}{\left( x_{\ast }-x\right)^{\alpha }}\right] ^{\frac{1}{1-\alpha }}. [/math]

Задача содержит производные второго порядка по пространственной координате и первого порядка по времени. Следовательно, необходимо поставить два граничных и одно начальное условие. Граничные условия следующие: первое - это условие нулевого раскрытия на фронте трещины , оно будет удовлетворено автоматически, т.к. решение уравнения упругости ищется в соответствующеем классе функций. Второе граничное условие --- это заданный в источнике ([math]x=0[/math]) поток [math]Q=2q_{0}[/math]. Множитель [math] 2 [/math] учитывает, что задача симметрична относительно начала координат. В терминах скорости частиц и раскрытия оно может быть записано в виде

[math] w\left( 0\right) v\left( 0+\right) =q_{0}. [/math]

Использование предела скорости справа учитывает, что в точке [math]x=0[/math] скорость имеет конечный разрыв ([math]v\left(0+\right) =-v\left( 0-\right) [/math]). В качестве начальных условий в момент времени [math]t_0[/math] необходимо задать начальное раскрытие [math] w_0(x) [/math] и начальную полудлину трещины [math] x_{*0} [/math]:

[math] w(x,t_{0})=w_{0}(x) \qquad \qquad \left\vert x\right\vert \leq x_{\ast }(0), [/math]

[math]x_{\ast }(0)=x_{\ast 0}. [/math]

Результаты численного моделирования

В рамках работы к решению задачи применялись следующие численные методы:

• метод Рунге-Кутты 4-го порядка;
• метод Адамса по схеме предиктор-корректор.

Выбор устойчивого численного метода, дающего точный результат за минимальное время является важным для применения модифицированной постановки к трехмерной задаче.

Метод Рунге-Кутты 4 порядка

Одним из наиболее распространенных методов Рунге-Кутты является метод 4 порядка точности. Для задачи Коши

[math] y^\prime = f(x,y), \ \ \ \ \ y(x_0) = y_0 [/math]

приближенное решение [math] y_{n+1} [/math] может быть найдено по следующей формуле:

[math] y_{n+1} = y_n + \frac{h}{6}\left(k_1 + k_2 + k_3 + k_4\right), [/math]

где

[math] k_1 =f(x_n,y_n), [/math]

[math]k_2=f\left(x_n + \frac{h}{2}, y_n + \frac{h}{2}k_1\right),[/math]

[math]k_3=f\left(x_n + \frac{h}{2}, y_n + \frac{h}{2}k_2\right),[/math]

[math]k_4=f\left(x_n + h, y_n + hk_3\right).[/math]

Для использования этого метода необходимо было найти максимальный шаг по времени, при котором сохраняется устойчивость метода. В дальнейшем шаг по времени может быть увеличен вместе с увеличением размера сетки, т.к. в условие устойчивости входит отношение [math] \Delta t / \Delta x^2 [/math].

Метод Адамса по схеме предиктор-корректор

Методы Адамса относятся к категории многошаговых конечно-разностных методов, т.е. для вычисления нового значения функции используют значения, вычисленные на предыдущих шагах. Существует две группы методов Адамса: явные методы Адамса (методы Адамса-Башфорта) и неявные (методы Адамса-Мультона). Неявная схема интегрирования предполагает итерационное решение системы. Итерационный процесс требует начального приближения решения. Его можно получить, использовав явную схему. Схема предиктор-корректор состоит из явной схемы, которую называют предиктором, и неявной, которую называют корректором. В рамках данной работы в качестве предиктора использовался метод Адамса-Башфорта 4-го порядка

[math] y_{n+1} = y_n + \frac{h}{24} \left(55f(t_{n}, y_n) - 59f(t_{n-1}, y_{n-1}) + 37f(t_{n-2}, y_{n-2}) - 9f(t_{n-3}, y_{n-3})\right), [/math]

а в качестве корректора --- метод Адмаса-Мультона 5-го порядка

[math] y_{n+1} = y_n + \frac{h}{720} (251f(t_{n+1}, y_{n+1}) + 646f(t_{n}, y_{n}) - 264f(t_{n-1}, y_{n-1}) + 106f(t_{n-2}, y_{n-2}) - 19f(t_{n-3}, y_{n-3}). [/math]

Использование такого метода решения системы ОДУ имеет то достоинство, что, будучи неявным, он более устойчивый и позволяет выбрать больший шаг интегрирования по времени.

Численные результаты и их обсуждение

В ходе моделирования основное внимание уделялось двум величинам: раскрытию трещины в источнике и ее полудлине. Контроль точности осуществлялся с использованием раскрытия и полудлины трещины, полученных из автомодельного решения. Это позволяло контролировать точность численного решения в последующие моменты времени путем сравнения результатов с автомодельным решением. Моделирование проводилось с момента времени [math] t_0 = 1[/math] до [math] t_{fin} = 100 [/math].

C целью выбрать наиболее эффективный метод проводилось сравнение использованных численных методов по устойчивости, точности и требуемым вычислительным затратам.

Расчеты проводились с разными сетками [math] M=21\ldots141[/math]. Проведенные численные эксперименты показали, что для устойчивости метода Рунге-Кутты необходимо выбирать меньший шаг интегрирования по времени, чем для метода Адамса по схеме предиктор-корректор.

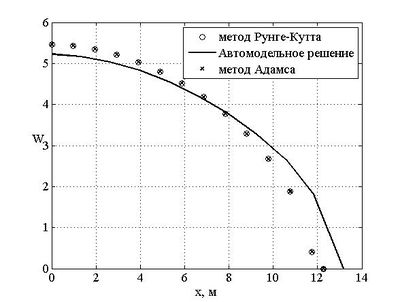
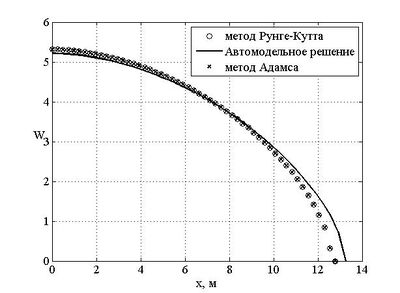
Результаты экспериментов показали, что оба метода дают результат с одинаковой точностью независимо от размера сетки. Для примера на рисунках

Результаты моделирования в момент времени [math]t_{fin}=100[/math] при [math]N=21[/math]

Результаты моделирования в момент времени [math]t_{fin}=100[/math] при [math]N=81[/math]

представлены результаты моделирования до времени [math] t_{fin} = 100 [/math] с использованием сетки с [math] M+1 = 21 [/math] и [math] M+1 = 81 [/math] узлами. Точки графика с равной нулю ординатой отвечают полудлине трещины, с равной нулю абсциссой - раскрытию в источнике.

Для сравнения вычислительных затрат и возможности их снижения в качестве исходной величины бралось время, которое необходимо для решения задачи на сетке с [math] M+1 = 41 [/math] узлом. Метод Рунге-Кутты без ускорения (т.е. без увеличения шага по времени вместе с увеличением масштаба сетки) требует одного часа для проведения моделирования до времени [math] t_{fin} = 100 [/math] в среде Matlab на ноутбуке Lenovo ideapad z710 с процессором Intel i5. Использование возможности увеличивать шаг по времени снижает это время до [math] 10 [/math] минут. Применение к решению задачи метода Адамса позволяет снизить время вычислений до [math] 5 [/math] минут. Существенно большие затраты времени при интегрировании методом Рунге-Кутты объясняются тем, что для его устойчивости требуется маленький шаг интегрирования по времени.

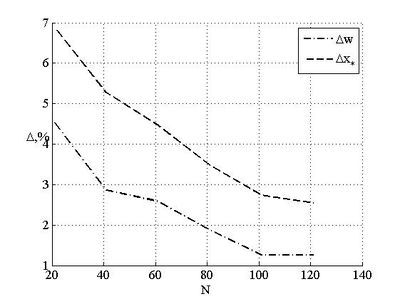
На рисунке

Погрешность решения в момент времени [math] t_{fin} = 100 [/math] в зависимости от числа узлов.

изображена зависимость погрешности решения от количества узлов сетки. Хорошо видно, что погрешность убывает с увеличением числа узлов, используемых для моделирования. Стоит отметить, что в сравнении с результатами работы А. М. Линьков 2016 погрешность заметно выросла (в работе А. М. Линьков 2016 погрешность вычисления полудлины не превышала [math] 1\% [/math] даже для сетки с [math] M + 1 = 21 [/math]). Возрастание погрешности объясняется тем, что в работе А. М. Линьков 2016 задача решалась в нормированных координатах. При использовании таких координат частная производная от раскрытия по времени равна нулю у вершины трещины ([math] \partial w / \partial t = 0 [/math]), тогда как в ненормированных координатах производная сингулярна: она имеет порядок сингулярности [math]O(\left( x_{\ast}-x\right) ^{\alpha -1})[/math], причем [math] \alpha \lt 1[/math].

Было проведено исследование зависимости решения от индекса поведения жидкости [math] n [/math].

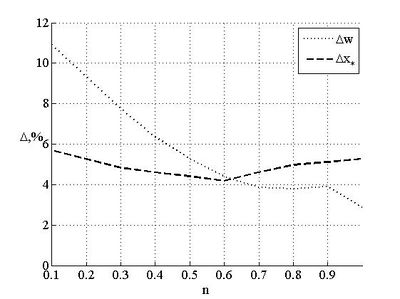
Величина обратная индексу поведения жидкости входит в уравнения Пуазейля и скорости как показатель степени, поэтому при стремлении [math] n [/math] к нулю, можно ожидать снижения точности решения. Погрешность вычислений для разных [math] n [/math] представлена на рисунке

Точность решения в момент времени [math] t_{fin} = 100 [/math] в зависимости от индекса поведения жидкости [math] n [/math]

. Из графика, представленного на рисунке, видно, что погрешность раскрытия в источнике существенно зависит от индекса поведения жидкости, а при его стремлении к нулю погрешность увеличивается в несколько раз. Эту погрешность можно устранить, перестроив алгоритм. Однако, это лежит в стороне от главной темы этой работы. Кроме того, в практике гидроразрыва обычно применяются жидкости с индексом поведения, превышающим [math] 0.5 [/math] , т.е. из диапазона, в котором метод обеспечивает достаточную точность.