Идентификация параметров пороупругой среды на примере бетонной плотины

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Р. Л. Лапин
Руководитель: ассистент кафедры ТМ С. А. Ле-Захаров

Введение

На сегодняшний моделей позволяющих просто и качественно описывать поведения материалов, имеющих в своем строении трещины и швы, в которых может находится газ или жидкость нет. Однако, необходимость в такой модели есть во многих технических областях. Ярким примером является анализ поведения плотины и грунта под ней под действием внешних факторов, например, воды в водохранилище.

Постановка задачи

Для материалов пористой структуры существует несколько моделей, например известные модели грунтов. Однако применимость их к материалам имеющих в своем строении трещины и швы остается под вопросом. Цель данной работы:

• Построить на базе модели пористой среды модель для бетона
• Провести сравнение с экспериментальными данными
• Проанализировать полученные результаты.

Обработка экспериментальных данных

Экспериментальные основаны на данных полученных с датчиков, расположенным в Саяно-Шушенской ГЭС. Датчики-пьезометры, измеряющие давление. Всего датчиков около 140, данные собираются с регулярностью 3-5 раза в месяц на протяжении последних 15 лет. Обработка данных с датчиков разделяется на два этапа: корреляционный анализ, и регрессионный анализ.

Расположения датчиков. Вид сверху

Корреляционный анализ

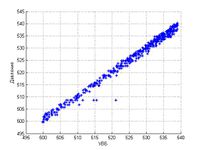
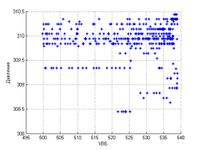
Корреляционный анализ позволяет определить зависит по набору данных зависит ли одна величина от другой. В ходе работы было выяснено, что разумнее всего исследовать зависимость показаний пьезометров от уровня воды в верхнем водохранилище - УВБ. Характеристикой зависимости был выбран коэффициент корреляции Спирмена.

[math] p \ = 1 - 6\frac{\sum{d}}{n^3-n}, p \in [-1; 1][/math]

Где [math]d[/math] - разность рангов величин взятых по одному из наборов данных для которых применяется анализ.

Значения коэффициента Спирмена близкое по модулю к [math]1[/math] говорит о том, что две величины зависят друг от друга. Значение близкое к [math]0[/math] говорит о независимости величин.

Показания датчиков соответствующие p=0.98

Показания датчиков соответствующие p=0.03

Пример линейной регрессионной модели

Пример квадратичной регрессионной модели

По результатам анализа был проведен отбор датчиков, которые можно считать хорошо работающими.

Регрессионный анализ

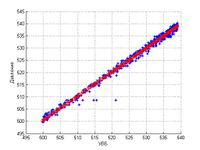
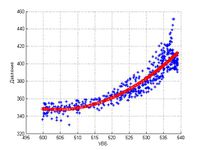
Для датчиков, которые удовлетворили корреляционному анализу была найдена модель зависимости показаний от УВБ. Метод решения этйо задачи регрессионный анализ.

Его идея в том, что для набора величин [math](X; Y)[/math] составляется предположительный вид зависимости, в данной работе полиномиальный [math]\bar{y} = a_0x^n+a_1x^{n-1}+...a_{n-1}x+a_n[/math]. Затем, для нахождения неизвестных коэффициентов [math]a_i[/math] используется метод наименьших квадратов. Строится функционал невязки [math] I= \sum{(\bar{y}(x_i)-y_i})[/math]. От которого беруться производные от [math]a_i[/math] и приравниваются к [math]0[/math]. В итоге получается линейная [math]n[/math]-мерная система относительно [math]n[/math] неизвестных, из которой находятся коэффициенты [math]a_i[/math].

В данной работе использовался линейный и квадратичный вид зависимости.