КП: Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения(моделирование эллипсоида)

А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения (моделирование эллипсоида)

---

Курсовой проект по Теоретической механике

Исполнитель: Лапин Руслан

Группа: 07 (20510)

Семестр: весна 2013

Аннотация проекта

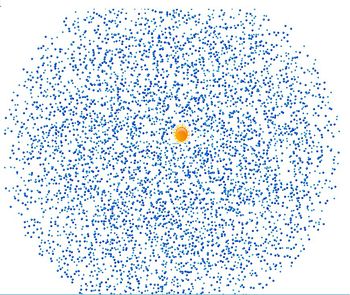
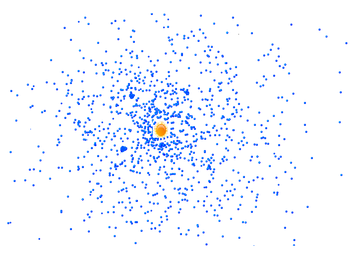
В основу данного курсового проекта положен проект "Земля-Луна", выполненный А.М.Кривцовым и А.А, Ле-Захаровым. В рамках данного курсового проекта исследуется возможное появление Солнечной системы из газопылевого облака, путем моделирования облака(эллипсоида) частиц, в поле массивного центрального тела (Солнца), которое расположено в центре системы.

Постановка задачи

Смоделировать систему облака частиц в центральном поле массивного тела (Солнца). Оценить правдоподобность гипотезы о появлении Солнечной системы из газопылевого облака.

Общие сведения по теме

Внесение массивного центрального тела влечет за собой необходимость перерасчета начальных данных, в частности угловой скорости вращения облака [math]\omega[/math]. Это имеет важную роль в дальнейшем исследовании, так как задав её, например, меньше нужной, получится так, что все частица "упадут" на Солнце. Выбрав же больше нужной, получится так, что все частицы разлетятся. И только при нужной нам, получится стабильное облако, дальнейшее развитие которого может привести к образованию модели Солнечной системы.

Решение

Начальное состояние, 10 тысяч частиц

Без учета солнца на частицу действуют следующие силы:

[math]\overline{F} = \overline{F}_{gr} + \overline{F}_{dis} + \overline{F}_{react}[/math]

где [math]F_{gr} = - G\frac{m^2}{r^2}[/math] гравитационная составляющая.

где [math]F_{dis} = -G\frac{m^{2}a^{11}\beta r'}{r^{14}}[/math] диссипативная составляющая.

где [math]F_{react} = G\frac{m^{2}a^{11}}{r^{13}}[/math] реактивная составляющая.

а [math]\gamma[/math] -гравитационная постоянная.

[math]m[/math] - масса частицы

[math]a[/math] - равновесное расстояние

[math]r[/math] - расстояние между частицами

[math]\beta[/math] - коэффициент диссипации

При внесении массивного тела массы [math]M[/math], возникает центральное поле и на частицы начинает действовать сила

[math]F = G\frac{mM}{R^2}[/math], где [math]m[/math] - масса частицы, [math]R[/math] - расстояние до частицы.

Для равномерного движения по окружности частица должна иметь угловую скорость, такую чтобы

[math] m\omega^2 R = G\frac{mM}{R^2}[/math]

То есть угловая скорость от появления центрального тела, должна быть

[math]\omega = \sqrt{G\frac{M}{R^3}}[/math]

А тогда учитывая еще и твердотельное вращение получаем искомую угловую скорость

[math]\omega = \sqrt{G\frac{M}{R^3}} + \sqrt{\frac{3 \pi GNm}{4R^3}}[/math]

где

[math]\omega_0 = \sqrt{\frac{3 \pi GNm}{4R^3}}[/math]

составляющая возникающая из-за присутствия твердотельного вращения (частицы движутся, как твердое тело).

Обсуждение результатов и выводы

10 тысяч частиц, результат после 15 тысяч итераций

В результате моделирования получилось стабильное облако частиц, которое вращается вокруг солнца. Начали образовываться небольшие кластеры, что свидетельствует о правильности модели и метода моделирования. Далее возможно исследование системы в зависимости от начальных параметров. Например увеличение числа частиц, изменение скоростей частиц, и наблюдение как будут меняться результаты.

Ссылки по теме

Проект "Земля - Луна"

См. также

• Справочная информация
• Курсовые проекты 2012
• Курсовые проекты 2013