Моделирование динамики толпы в областях со сложной геометрией
Введение
В работе исследуются способы более оптимальной организации движения людей, особенно в условиях паники – ведь в таком случае появляется большой риск получения людьми увечий вследствие увеличения «давления» в толпе.
Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек.
Цель
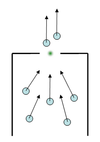
Цель работы – смоделировать и исследовать движение толпы при различных условиях, найти лучшие способы организации движения в таких местах, как проход в метрополитен, фойе театра, проход в концертный зал, и в других местах, предполагающий переход большого количества людей через некий узкий проём.
Реализация
Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL. Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса – частицы отталкиваются друг от друга, но не притягиваются. Чтобы смоделировать стремление людей попасть в определенную область – на моделирующей области задано векторное поле сил, устремляющее частицу к «выходу»
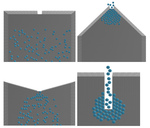
Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области.
Для оценки ситуации измеряются две величины – время прохождения частиц через отверстие, и давление, возникающее в группе частиц. Требуется достичь минимального времени, однако при этом давление не должно превышать некоторого критического значения – чтобы максимально снизить риск травмирования людей в толпе.
Для расчета давления в системе, используется формула из главы «Техника моделирования» книги А. М. Кривцова «Деформирование и разрушение твердых тел с микроструктурой».
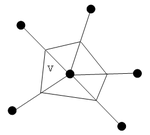
где d – размерность задачи (в нашем случае d = 2), Fα - воздействие на частицу от окружающих её частиц α, Aα – расстояние от рассчитываемой частицы до окружающих её частиц, V – собственное пространство частицы (площадь многоугольника, построенного на половинах расстояний до ближайших частиц)
Для визуализации давлений, действующих на частицу, используется цвет этой частицы – чем больше давление, тем больше смещение к красному концу спектра