Моделирование гидроразрыва пласта

Схема гидроразрыва

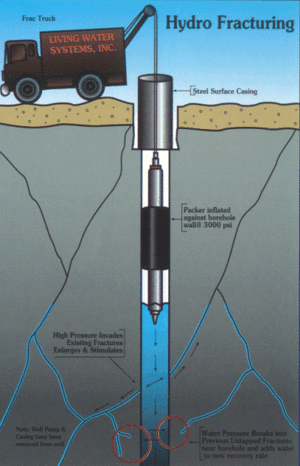
Гидравлический разрыв пласта

Гидроразры́в пласта́ (ГРП) — один из методов интенсификации работы нефтяных и газовых скважин и увеличения приёмистости нагнетательных скважин. Метод заключается в создании высокопроводимой трещины в целевом пласте для обеспечения притока добываемого флюида (газ, вода, конденсат, нефть либо их смесь) к забою скважины. Технология осуществления ГРП включает в себя закачку в скважину с помощью мощных насосных станций жидкости разрыва (гель, в некоторых случаях вода, либо кислота при кислотных ГРП) при давлениях выше давления разрыва нефтеносного пласта. Для поддержания трещины в открытом состоянии в терригенных коллекторах используется расклинивающий агент — проппант, в карбонатных — кислота, которая разъедает стенки созданной трещины.

A ‘‘typical’’ hydraulic fracturing treatment starts with the creation of an initial path for the fracture. This is usually achieved by a technique called ‘‘perforation’’ in which specially designed shaped-charges are blasted on the wellbore walls with given orientations, perforating the casing and creating finger-like holes or weak points in the hydrocarbon-laden formation. A viscous fluid is pumped inside the wellbore, inducing a steep rise in the pressure which eventually leads to the initiation of a fracture at the perforated interval. A ‘‘pad’’ of clean fluid is usually pumped first, to provide sufficient fracture width for the proppant that follows. Proppant is injected at a later stage as a suspension or slurry. The treatment usually takes place on a time-scale of tens of minutes to a few hours, depending upon the designed fracture size and volume of proppant to be placed. At the end of the treatment, when pumping stops, leak-off of the residual fracturing fluid into the porous reservoir allows the fracture surfaces to close onto the proppant pack under the action of the far-field compressive stresses.

Физические процессы, сопровождающие гидроразрыв

Основные процессы:

• the mechanical deformation induced by the fluid pressure on the fracture surfaces
• the flow of fluid within the fracture
• the fracture propagation.

Additional complications

• the presence of layers of different types of rock (even if these layers are assumed to be parallel);
• changes in magnitude and/or orientation of the in situ confining stresses;
• the presence of a nearby free surface (of importance in the modeling of magma-driven dykes and in caving applications in mining);
• the leak-off of fracturing fluid from the fracture to the surrounding rock (or the invasion of reservoir fluid from the rock into the fracture), which is a history-dependent process;
• the effects of shear and temperature on the fracturing fluid rheology;
• the transport of suspended proppant particles within the fracture (of primary importance for oil and gas reservoir stimulations);
• modeling of fracture recession and closure (due to termination of pumping, forced flowback, or rapid geometric changes in one region as fractures herniate into other lower stress zones).
• hydraulic fracturing in so-called ‘‘soft’’ formations, such as weakly consolidated sandstones that are prone to non-linear mechanical failure—a real challenge for current models that are based on the principles of LEFM.

Методы, используемые в литературе

Моделирование разрушения горной породы

Для моделирования разрушения горной породы в процессе гидроразрыва используются как методы механики сплошной среды (метод конечных элементов, метод граничных элементов), так и механики дискретных сред (метод дискретных элементов).

При использовании континуальных методов, как правило, вводятся следующие ограничения:

• the host reservoir material is considered to be linear elastic;
• in the case of a multi-layered reservoir, the layer interfaces are assumed to lie parallel to each other and to be perfectly bonded;
• the hydraulic fracture is assumed to lie in a single vertical plane;

Что не учитывается?

• plastic behavior of the host rock;
• nonparallel and debonded interfaces
• and non-planar fractures
• the actual reservoir may be naturally fractured;
• the actual reservoir may contain a heterogeneous stress field due to poroelastic influences of neighboring producing wells;

S.A.G. Torres and J.D.M.Castaño Simulation of the hydraulic fracture process in two dimensions using a discrete element method// Phys. Rev. E 75, 066109, 2007.

We introduce a discrete element simulation for the hydraulic fracture process in a petroleum well which takes into account the elastic behavior of the rock and the Mohr-Coulomb fracture criterium. The rock is modeled as an array of Voronoi polygons joined by elastic beams, which are submitted to tectonical stresses and the hydrostatic pressure of the fracturing fluid. The fluid pressure is treated like that of a hydraulic column. We also include an analysis of the fracturing fluid loss due to the permeability of the rock which is useful in an efficiency analysis of the treatment. �

S. Deng, R. Podgorney, H. Huang, Discrete Element Modeling of rock deformation, fracture network development, permeability evolution under hydraulic stimulation // Proc. 36 Workshop on Geothermal reservoir engineering, 2011.

• 3D discrete element method with bonded particle model (BPM)
• two way coupling with fluid dynamics (model for network fluid flow)

J.P. Pruiksma, A. Bezuijen Hydraulic fracturing with distinct element method // Report of DELFRAC consortium, 2002

In this report, hydraulic fracturing is investigated using the distinct element code PFC2D from Itasca. Special routines adding fluid flow to PFC2D and updating the fluid flow domains when fractures appear. After the set-up of the hydraulic fracturing simulations has been discussed, with all the main input parameters, several main parameters are varied to study the resulting fracture patterns, pressure distributions and borehole pressures. These parameter studies are: particle size dependency of the simulations, behaviour at various confining stresses, the influence of the internal friction angle of the sand and the fracturing behaviour for different borehole injection rates. After this parameter study, comparisons are made with experiments done at TU Delft, GeoDelft and in the literature. The simulation results show the same trends as the experiments and are also in good agreement quantitatively.

Моделирование течения жидкости в трещинах гидроразрыва

• usually, the fluid flow equations are restricted to relatively simple models for the fluid rheology, such as Newtonian or power-law. However, actual fluids used for hydraulic fracturing treatments have more complicated rheologies (yield stresses, viscoelasticity, etc.);
• the fluid flow in the fracture obeys Poiseuille flow and is incompressible, sequential injections of multiple fluids are immiscible.
• leak-off is often assumed to be uncoupled from the fluid pressure, and to be restricted to the linear (1D) flow regime;

Моделирование динамики проппанта

The transport and placement of proppant within the fracture is usually modeled by representing the slurry (i.e., the mixture of proppant and fluid) as a two-component, interpenetrating continuum. The distribution of proppant in the fracture is given by its volumetric concentration (defined as the probability of finding a proppant particle at a given point in space and time), which is the additional variable to be determined. In modeling proppant transport and placement, it is often assumed that:

• both proppant and fluid are incompressible;
• the proppant particles are small compared to a characteristic lengthscale, in this case the fracture width;
• the only mechanism to account for ‘‘slip’’ between the proppant and the carrying fluid is gravity-induced settling, i.e., relative proppant-fluid velocities due to migration by self-diffusion (created by shearing and/or proppant collision), Taylor dispersion, or clustering are usually neglected. This implies that, in the absence of gravity, the proppant and fluid move at the same velocity at any given point.
• interaction and collision between proppant particles, shearinduced proppant migration, proppant settling, etc.

Литература

1. Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 (download, pdf)