Курсовой проект по Механике дискретных сред
Исполнитель: Исаева Сабина
Группа: 3630103/60101
Семестр: осень 2019
Постановка задачи
1) Сравнить различные методы интегрирования уравнений движения одномерной линейной цепочки (Верле, Рунге-Кутта).
Реализовать фиксированные, свободные и периодические граничные условия.
2) Рассмотреть движение частицы в потенциальной яме Леннарда-Джонса: численно определить скорость диссоциации.
Первая задача
Первая задача: решение
Уравнение движения:
[math] \dot{v} = w^2 (x_{i+1} - 2x_{i} + x_{i-1}) [/math]
[math] \dot{x} = v [/math]
Первая задача: метод Верле
[math] v_{i+1} = v_i + w^2 (x_{i+1} - 2x_{i} + x_{i-1})\Delta t [/math]
[math] x_{i+1} = x_i + v_{i+1}\Delta t [/math]
Первая задача: метод Рунге-Кутта 4 порядка
[math] v_{i+1} = v_i + \frac {g_1 + 2g_2+2g_3+g_4}{6}[/math]
[math] x_{i+1} = x_i + \frac {k_1 + 2k_2+2k_3+k_4}{6}[/math]
Где
[math] g_{1(i,j)} = h F(u_{i,j - 1}, u_{i,j}, u_{i,j + 1})[/math]
[math] g_{2(i,j)} = h F(u_{i,j - 1} + \frac {g_{1(i,j-1)}}{2}, u_{i,j} + \frac {g_{1(i,j)}}{2}, u_{i,j + 1} + \frac {g_{1(i,j+1)}}{2})[/math]
[math] g_{3(i,j)} = h F(u_{i,j - 1} + \frac {g_{2(i,j-1)}}{2}, u_{i,j} + \frac {g_{2(i,j)}}{2}, u_{i,j + 1} + \frac {g_{2(i,j+1)}}{2})[/math]
[math] g_{4(i,j)} = h F(u_{i,j - 1} + g_{3(i,j-1)}, u_{i,j} + g_{3(i,j)}, u_{i,j + 1} + g_{3(i,j+1)})[/math]
[math] k_{1} = h v_{i,j}[/math]
[math] k_{2} = h (v_{i,j} +\frac {k_{1}}{2})[/math]
[math] k_{3} = h (v_{i,j} +\frac {k_{2}}{2})[/math]
[math] k_{4} = h (v_{i,j} + k_{3})[/math]
[math] F = w^{2}(x_{i,j+1} -2 x_{i,j} + x_{i,j-1})[/math]
Первая задача: граничные условия
Фиксированные граничные условия:
[math] v_{i+1,1} = 0[/math]
[math] v_{i+1,N} = 0[/math]
[math] x_{i+1,1} = 0[/math]
[math] x_{i+1,N} = 0[/math]
Свободные граничные условия:
[math] v_{i+1,1} = v_{i,1} + w^2 (x_{i,2} - x_{i,1})\Delta t[/math]
[math] v_{i+1,N} = v_{i,N} + w^2 (x_{i,N - 1} - x_{i,N})\Delta t[/math]
Периодические граничные условия:
[math] v_{i+1,1} = v_{i,1} + w^2 (x_{i,2} - 2x_{i,1} + x_{i,N})\Delta t[/math]
[math] v_{i+1,N} = v_{i,N} + w^2 (x_{i,N - 1} - 2x_{i,N} + x_{i,1})\Delta t[/math]
Первая задача: результат
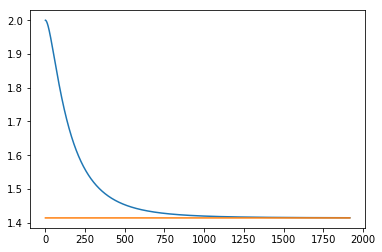
Orange Line- Метод Рунге -Кутта
Blue Line-Метод Верле
Метод Верле и Метод Рунге-Кутта с фиксированными границами:
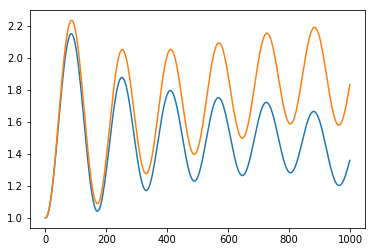
Метод Верле и Рунге -Кутта с периодическими граничными условиями:
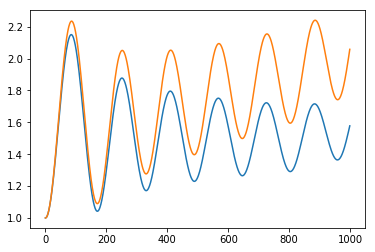
Метод Верле и Метод Рунге-Кутта 4 порядка со свободными границами:
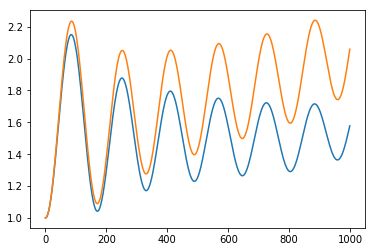
Вторая задача
Вторая задача: решение
Уравнение движения частицы в потенциальной яме Леннарда-Джонса:
[math] v_{i+1} = v_i + F_{r}(x_i)\Delta t [/math]
[math] x_{i+1} = x_i + v_i \Delta t [/math]
Где
[math] F_{r}(x_i) = \frac{12D(-(\frac{a}{x})^{13} + (\frac{a}{x})^{7})}{a}[/math]
Вторая задача: дополнительные данные
Начальное положение частицы:
[math] x = 1.2.[/math]
Вторая задача: результат
Частица в потенциальной яме Леннарда-Джонса: