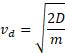"Численные методы интегрирования уравнений движения для одномерной линейной цепочки и частицы в потенциальной яме Леннарда-Джонса"

Курсовой проект по Механике дискретных сред

Исполнитель: Троцкая Валерия

Группа: 3630103/60101

Семестр: осенний семестр 2019-2020 учебного года

Постановка задачи:

1. Сравнить различные методы интегрирования уравнений движения (Верле, Рунге-Кутта 4 порядка). Реализовать фиксированные, свободные и периодические условия
2. Численно определить скорость диссоциации частицы в потенциальной яме Леннарда-Джонса

Теоретическая сводка:

1. Одномерная линейная цепочка

Рассмотрим модель колебаний одинаковых атомов массой m, находящихся в одномерной цепочке. Пусть в этой цепочке находится N атомов, связанных между собой квазиупругой силой с коэффициентом упругости k.

Если учитывать взаимодействие только соседних атомов, уравнение движения можно записать в следующем виде:

Для решения уравнения движения воспользуемся численными методами интегрирования:

а. Метод Верле

б. Метод Рунге-Кутта 4 порядка

Для каждого из методов реализуются 3 вида граничных условий:

• Фиксированные граничные условия

• Свободные граничные условия

• Периодические граничные условия

2. Частица в потенциальной яме Леннарда-Джонса

Уравнение движения частицы в потенциальной яме Леннарда-Джонса:

Скоростью диссоциации будем называть скорость, которую необходимо сообщить частице, чтобы она улетела на бесконечность.