Машина Голдберга , машина Руба Голдберга , машина Робинсона-Голдберга , Машина Робинсона или заумная машина — это устройство, которое выполняет очень простое действие чрезвычайно сложным образом — как правило, посредством длинной последовательности взаимодействий по «принципу домино».
По принципу работы Машины Голдберга мы собираем установку "Фотоаппарат Голдберга".
Описание Актуальность Данный проект является актуальным за счет того, что при создании данной машины Голдберга можно найти практическое применение курсу теоретической механики, развить прикладные способности, а также научиться использовать разнообразное оборудование.
Цель проекта Воссоздать машину Голдберга, результатом работы которой будет осуществление фотоснимка.
Задачи проекта Обозначить последовательность действий, которые будут выполняться машиной Голдберга
Создать схему Машины Голдберга.
Создать цифровую модель данной установки
Подобрать необходимые материалы и инструменты для проекта
Сделать отдельные этапы проекта
Произвести необходимые расчеты и вычисления для определения параметров отдельных частей проекта.
Собрать воедино все этапы Машины Голдберга.
Произвести пробные запуски и устранить недочеты.
Смонтировать видео.
Произвести показательный запуск Машины Голдберга.
Создать вики-страницу проекта Проектная команда Группа 13131/8
Войтенко Мария
Вишнев Артем
Данилова Дарья
Доенина Анна
Егунова Анастасия
Ефимов Евгений
Лось Полина
Нахимовский Алексей
Панова Юлия
Савчиков Артем
Сиротина Анастасия
Филиппенкова Алина
Хайбулина Олеся
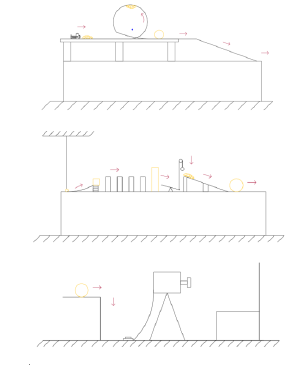
Шестаков Данил Работа по проекту Действия, выполняемые машиной Голдберга Схема устройства этапов Машины Голдберга, совершающей фотоснимок
Запуск резинки, толкающей машинку
Машинка совершает элемент "мертвая петля" на трассе
Машинка толкает шарик
Шарик скатывается по наклонной плоскости и толкает маятник
Маятник толкает домино
В процессе падают все доминошки
Последняя из домино толкает брусок
Брусок толкает машинку
Машинка толкает кубик
Кубик падает на рычаг
Рычаг поднимается с другой стороны
Блок перевешивает на другую сторону
Груз блока толкает шарик
Шарик катится и падает на кнопку
Совершается фотоснимок Материалы и предметы для создания проекта Мячики
Элемент "мертвая петля"
2 машинки
Рычаг
Нить
Фанера
Доски
Клей
Кегля
Стул
Неподвижный блок
Резинка
Кнопка дистанционного управления
Домино
Скотч Инструменты для создания проекта Этапы создания проекта
Срок
Задачи
Возникающие проблемы
Что сделано к сроку
05.03.19
Обсуждение этапов работы Машины Голдберга
Возникновение разногласий по поводу последовательности действий, этапов машины
Нахождение оптимальной схемы машины, создание чернового варианта модели
19.03.19
Утверждение этапов модели, создание списка материалов и распределение по мини-группам
Неравномерное распределение по группам; прения по поводу того, на чем будет машина стоять, сколько места займет и на каких этапах потребуются более высокие конструкции
Определение наиболее подходящего распределения по группам, распределение задач и постановка целей; нахождение компромисса по поводу спорных моментов
02.04.19
Нахождение материалов, создание начальных этапов
Проблематичность обеспечения некоторыми изначально включенными в список материалами, количество провальных запусков машины на первых этапах, преобладавшее над удачными
Замена труднодоставаемых материалов другими ("мёртвой" петли, изначально планировавшейся быть напечатанной на 3D-принтере, на установку из детского набора), возникновение понимания того, как лучше всего дать машинке старт, создание "бортиков" на 2 этапе, дабы обеспечить удачный спуск машинки
15.04.19
Окончательное создание первых этапов установки и контроль их работы
Неполная работоспособность установки, в следствие чего возникла необходимость замены некоторых материалов
Первые этапы установки находятся в рабочем состояние примерно на 75%
16.04.19
Сбор отдельных этапов установки, требующих наиболее прикладную составляющую, и проверка их на работоспособность, примерный расчёт необходимых параметром для этих этапов
Нехватка материалов, поэтому необходимость докупать материалы; появление необходимости получения навыков работы с прикладными инструментами
Первые этапы установки готовы и работают в идеальном состоянии, частично созданы последующие этапы машины
29.04.19
Сбор всех этапов установки в единое целое, проверка их работоспособности
Наличие недочетов в работе установки
Установка практически приобрела свой окончательный вид
30.04.19
Повторный, полный сбор установки с устранением выявленных неполадок
Практически не возникло, были убраны небольшие недочеты, чтобы установка работала каждый раз в штатном режиме
Окончательно готовая установка
14.05.19
Проведение контрольных запусков машины, оформление вики-страницы
Трудности при создание вики-страницы из-за не знания языка программирования
Удачное прохождение машиной всех этапов, создание фотографий посредством её; приобретение необходимые знаний по оформлению вики-страницы, преодоление трудностей
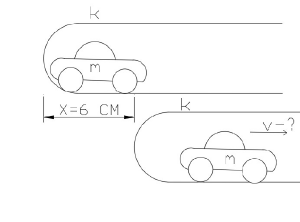
Расчёты элементов проекта Расчёт скорости машины, с которой она поедет при запуске пружины
[math]Дано:[/math] Схема для расчета скорости машины, с которой она поедет при запуске пружины
[math]k=0{,}1~кН/м[/math] [math]m=40~г[/math] [math]х=6~см[/math] [math]Найти:~v[/math] [math]Решение:[/math] [math]Согласно ~закону ~сохранения ~энергии ~при ~отсутствии ~неконсервативных ~сил ~полная ~механическая ~энергия ~системы ~тел ~сохраняется.[/math] [math]E=const E _{1}=E _{2}[/math] [math]Конечная ~энергия ~системы ~определяется ~только ~кинетической ~энергией ~машинки, ~которая ~определяется ~по ~формуле:[/math] [math]E _{2}=\frac{(m\cdot v^2)}{2}[/math] [math]Начальная ~энергия ~системы ~определяется~потенциальной ~энергией ~растянутой ~резинки:[/math] [math]E _{1} = \frac{(k\cdot x^2)}{2} [/math] [math]В ~итоге:[/math] [math]\frac{(m\cdot v^2)}{2} = \frac{(k\cdot x^2)}{2}[/math] [math]v = x\cdot \sqrt{(\frac{k}{m}}) [/math] [math]v\approx3~м/c [/math] [math]Ответ:v\approx3~м/c. [/math]
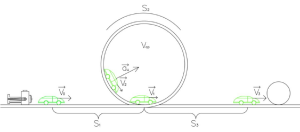
Расчёт скорости машинки при соударении с шариком
Схема прохождения машинки мертвой петли и соударения с шариком
[math]Дано:[/math] [math]v_{0}=2{,}8~м/c[/math] [math]t_{1}=0{,}125~c[/math] [math]t_{2}=0{,}375~c[/math] [math]t_{3}=0{,}125~c[/math] [math]S_{1}=0{,}36~м[/math] [math]S_{3}=0{,}155~м[/math] [math]R=0{,}1125~м[/math] [math]Найти:~v_{3}[/math] [math]Решение:[/math] [math]Расстояние, ~пройденное ~машинкой ~от ~пускового ~механизма ~до ~начала ~мертвой ~петли:[/math] [math]S_{1}=v_{0} \cdot t_{1}-\frac{a_{1} \cdot t_{1}^2}{2}[/math] [math]При ~этом, ~движение ~машинки ~будет ~равнозамедленным.[/math] [math]Найдем ~ускорение, ~такого ~движения: [/math] [math]a_{1}=\frac{v_{0} \cdot t_{1} \cdot 2}{t_{1}^2} - \frac{S_{1} \cdot 2}{t_{1}^2}[/math] [math]a_{1}=\frac {2{,}8 \cdot 0{,}125 \cdot 2}{0{,}125^2} - \frac {0{,}36 \cdot 2}{0{,}125^2}=-1{,}28~м/с^2[/math] [math]Пусть ~v_{1}- ~скорость ~машинки ~в ~самом ~начале ~петли, ~а ~v_{2}- ~в ~конце.[/math] [math]Выразим ~v_{1} ~через ~ускорение:[/math] [math] a_{1}=\frac{dv_{1}}{dt} [/math] [math] a_{1} \cdot (\int\limits_0^t_{1} \,dt)=(\int\limits_v_{0}^v_{1} \,dv) [/math] [math] a_{1}=\frac{v_{1}-v_{0}}{t_{1}} [/math] [math] v_{1}=a_{1} \cdot t_{1}+v_{0}[/math] [math] v_{1}=-1{,}28 \cdot 0{,}125+2{,}8=2{,}64 ~м/с[/math] [math]Ускорение ~машинки ~в ~мертвой ~петле:[/math] [math] a_{2}=a_{ц}= \frac {v_{ср}^2}{R}[/math] [math]v_{ср} - ~средняя ~скорость ~машинки ~при ~движении ~по ~петле.[/math] [math]S_{2} - ~расстояние, ~пройденное ~машинкой ~по ~мертвой ~петле.[/math] [math] v_{ср}= \frac {S_{2}}{t_{2}}= \frac {2 \cdot \pi \cdot R}{t_{2}}[/math] [math]Представим ~среднюю ~скорость ~как ~полусумму ~скоростей ~v_{1} ~и ~v_{2}:[/math] [math] v_{ср}= \frac {v_{1}+v_{2}}{2}[/math] [math] \frac{v_{1}+v_{2}}{2}= \frac {2 \cdot \pi \cdot R}{t_{2}}[/math] [math]Отсюда ~v_{2} ~будет:[/math] [math] v_{2}= \frac {4 \cdot \pi \cdot R-v_{1} \cdot t_{2}}{t_{2}}[/math] [math] v_{2}= \frac {4 \cdot 3{,} 14 \cdot 0{,}1125-2{,}64 \cdot 0{,}375}{0{,}375}=1{,}128 ~м/с[/math] [math]Расстояние, ~пройденное ~телом ~от ~конца ~мертвой ~петли ~до ~точки ~столкновения ~машинки ~с ~шариком:[/math] [math] S_{3}=v_{2} \cdot t_{3}-\frac {a_{3} \cdot t_{3}^2}{2}[/math] [math] a_{3}= \frac {2 \cdot v_{2} \cdot t_{3}-2 \cdot S_{3}}{t_{3}^2}[/math] [math] a_{3}= \frac {2 \cdot 1{,}128 \cdot 0{,}125-2 \cdot 0{,}155}{0{,}125^2}=-1{,}792 ~м/с^2[/math] [math]Таким ~образом, ~скорость ~машинки ~при ~ударе ~о ~шарик ~будет:[/math] [math] v_{3}=a_{3} \cdot t_{3}+v_{2}[/math] [math] v_{3}=-1{,}792 \cdot 0{,}125+1{,}128=0{,}904 ~м/с[/math] [math]Ответ:v_{3}=0{,}904~м/с.[/math]
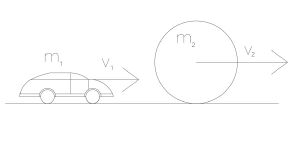
Расчёт скорости мяча, приобретенной в результате упругого соударения с машиной
Схема для расчёта приобретенной в результате упругого соударения с машиной скорости мяча
[math]Дано:[/math] [math]m_{1}=0{,}04~кг[/math] [math]m_{2}=0{,}056~кг[/math] [math]v_{1}=0{,}904~м/с[/math] [math]Найти:~v_{2}[/math] [math]Решение:[/math] [math]По~закону~сохранения~импульса~(ЗСИ):[/math] [math]p_{11}+p_{12}=p_{21}+p_{22} [/math] [math]p_{12}=0,~так~как~мяч~в~начале~покоится,~а~p_{21}=0,~так~как~машина~останавливается.~Следовательно: [/math] [math]m_{1} \cdot v_{1}=m_{2} \cdot v_{2} [/math] [math]Выражаем~скорость~шарика:[/math] [math]v_{2}=\frac{m_{1} \cdot v_{1}}{m_{2}} [/math] [math]Подставим~численные~значения: [/math] [math]v_{2}=\frac{0{,}04~кг \cdot 0{,}904~м/c}{0{,}056~кг} [/math] [math]v_{2}=0{,}65~м/с [/math] [math]Ответ:0{,}65~м/с [/math]
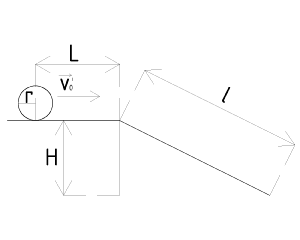
Расчёт скорости шара в конце наклонной плоскости
Расчет скорости шара в конце наклонной плоскости
[math]Дано:[/math] [math]L=15~см[/math] [math]H=13{,}3~см[/math] [math]l=29{,}8~см[/math] [math]r=3{,}1~см[/math] [math]v_{0}'=0{,}65~м/c[/math] [math]Найти:~v[/math] [math]Решение:[/math] [math]Для~решения~задачи~используем~формулу~(1):[/math] [math]v=\omega \cdot r~(1)[/math] [math]где~\omega=\beta \cdot t[/math] [math]\beta=\frac{M}{l}[/math] [math]Найдем~момент~внешних~сил~относительно~точки~касания~плоскости~и~шара.[/math] [math]Этот~момент~будет~обеспечиваться~только~силой~тяжести,~т.к.~остальные~моменты~будут~равны~0.[/math] [math]M=m \cdot g \cdot r \cdot sin\alpha[/math] [math]Найдем~I~(момент~инерции~шара~относительно~оси,~проходящей~через~точку~касания~плоскости)~при~помощи~теоремы~Штейнера:[/math] [math]I=I_{ц}+m \cdot r^2[/math] [math]Момент~инерции~относительно~центра~шара~вычисляется~следующим~образом:[/math] [math]I_{ц}=\frac{2}{5} \cdot m \cdot r^2[/math] [math]Таким~образом:[/math] [math]I=\frac{7}{5} \cdot m \cdot r^2[/math] [math]Подставив~полученные~выражения~в~формулу~(1),~получим:[/math] [math]v=\frac{5}{7} \cdot g \cdot t \cdot sin\alpha~(2)[/math] [math]Используя~формулы~(3)~и~(4),~выразим~время~(5):[/math] [math]S=\frac{v^2-v_{0}^2}{2 \cdot a}~(3)[/math] [math]a=\frac{v^2-v_{0}^2}{2 \cdot S}[/math] [math]v=v_{0}+a \cdot t~(4)[/math] [math]v=v_{0}+\frac{v^2-v_{0}^2}{2 \cdot S} \cdot t~(4)[/math] [math]t=\frac{2S}{v+v_{0}}~(5)[/math] [math]Подставим~(5)~в~(2):[/math] [math]v=\frac{5}{7} \cdot g \cdot \frac{2S}{v+v_{0}} \cdot sin\alpha~[/math] [math]v^2+v \cdot v_{0}-\frac{10}{7} \cdot g \cdot l \cdot \frac{H}{l}=0~(6)[/math] [math]Так~как~силой~трения~качения~в~условиях~данной~задачи~мы~пренебрегаем,~то~в~качестве[/math] [math]𝑣_{0}~мы~принимаем~v_{0}~-~скорость,~которую~сообщает~шару~машинка~в~предыдущей~задаче.[/math] [math]Подставим~численные~значения~в~формулу~(6):[/math] [math]700 \cdot v^2+455 \cdot v -1329{,}08=0[/math] [math]Решим~квадратное~уравнение,~получим~два~корня:[/math] [math]v_{1}=1{,}091~м/c[/math] [math]v_{2}=-1{,}741~м/c[/math] [math]Отрицательное~v~не~подходит~нам,~так~как~нас~интересует~модуль~скорости.[/math] [math]Поэтому~ответом~данной~задачи~является~v=1{,}091~м/c[/math] [math]Ответ:v=1{,}091~м/с[/math]
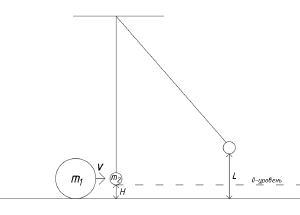
Расчёт оптимальной массы шарика, необходимой для поднятия после удара на высоту h
Расчет оптимальной массы шарика, необходимой для поднятия после удара на высоту h
[math]Дано:[/math] [math]m_{1}=0{,}056~кг[/math] [math]v=1{,}091~м/с[/math] [math]H=0{,}04~м[/math] [math]L=0{,}12~м[/math] [math]g=9{,}8~м/с^2[/math] [math]Найти:~m_{2}[/math] [math]Решение:[/math] [math]Шарик~массы~m_{2},~подвешенный~на~нити,~находится~на~некоторой~высоте~h,[/math] [math]которая~равна~L-H=0{,}12~м-0{,}04~м=0{,}08~м[/math] [math]На~него~налетает~мяч~массы~m_{1},~происходит~упругое ~соударение,[/math] [math]поэтому~запишем~закон~сохранения~импульса~(ЗСИ):[/math] [math]m_{1} \cdot v=m_{2} \cdot v',~где~v'-скорость~шарика~после~соударения.[/math] [math]v'=\frac{m_{1} \cdot v}{m_{2}}[/math] [math]Запишем~также~закон~сохранения~энергии(ЗСЭ)~для~шарика,~учитывая,~что~он~поднимется~на~высоту~h:[/math] [math]\frac{m_{2} \cdot v'^2}{2}=m_{2} \cdot g \cdot h[/math] [math]Подставив~v',~получим:[/math] [math]\frac{m_{2} \cdot m_{1}^2 \cdot v^2}{2 \cdot m_{2}^2}=m_{2} \cdot g \cdot h[/math] [math]Выразим~m_{2}:[/math] [math]m_{2}=\frac{m_{1} \cdot v}{\sqrt{2 \cdot g \cdot h}}[/math] [math]m_{2}=\frac{0{,}056~кг \cdot 1{,}091~м/с}{\sqrt{2 \cdot 9{,}8~м/с^2 \cdot 0{,}08~м}}=0{,}04~кг[/math] [math]Сравниваем ~с ~экспериментальным ~значением ~массы~и~видим,~что ~масса ~получилась ~подходящей[/math] [math]Ответ:m _{2}=0{,}04~кг.[/math]
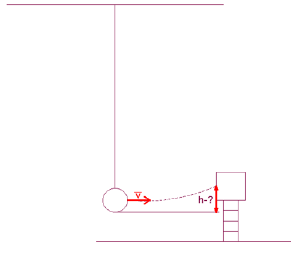
Расчёт оптимальной высоты подъема шарика
Расчет оптимальной высоты подъема шарика
[math]Дано:[/math] [math]v=1{,}2~м/с[/math] [math]g=9{,}8~м/с^2[/math] [math]Найти:~h[/math] [math]Решение:[/math] [math]Используем~закон~сохранения~энергии~(ЗСЭ)[/math] [math]E_{к}=E_{п}[/math] [math]\frac{m \cdot v^2}{2}=m \cdot g \cdot h[/math] [math]Получаем~значение~оптимальной~высоты~h:[/math] [math]h=\frac {v^2}{2g}=\frac {1{,}2^2}{2 \cdot 9{,}8}=0{,}07~м[/math] [math]Сравниваем~с~экспериментальным~значением~высоты,~которое~равно~0{,}064~м[/math] [math]Ответ:h=0{,}07~м[/math]
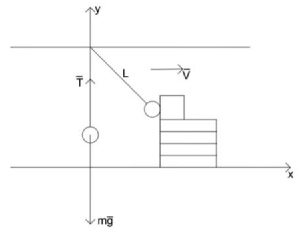
Расчёт скорости кубика, приобретённой в результате cоударения с шариком на нити
Расчет скорости кубика, приобретенной в результате соударения с шариком на нити
[math]Дано:[/math] [math]m=0{,}009~кг[/math] [math]M=0{,}016~кг[/math] [math]g=9{,}8~м/c^2[/math] [math]\left | \vec{T} \right |=0{,}2~Н[/math] [math]L=0{,}2~м[/math] [math]Найти:~v_{кубик}[/math] [math]Решение:[/math] [math]Обозначим~массу~шарика~через~m,~а~массу~кубика~через~M. [/math] [math]По~второму~закону~Ньютона~в~проекциях~на~ось~Oy~инерциальной~системы~отсчёта~Oxy: [/math] [math]\frac{m \cdot v_{шарик}^2}{L}=T-m \cdot g[/math] [math]Следовательно:[/math] [math]v_{шарик}=\sqrt{(\frac{T}{m}-g) \cdot L}[/math] [math]Происходит~упругое~соударение.~По~закону~сохранения~импульса~(ЗСИ):[/math] [math]m \cdot v_{шарик}=M \cdot v_{кубик} [/math] [math]Соответственно~скорость~кубика~равна:[/math] [math]v_{кубик}=\frac{m \cdot v_{шарик}}{M}=\frac{m \cdot \sqrt{(\frac{T}{m}-g) \cdot L}}{M}[/math] [math]Получим~численное~значение:[/math] [math]v_{кубик}=\frac{0{,}009~кг \cdot \sqrt{(\frac{0{,}2~Н}{0{,}009~кг}-9{,}8~Н) \cdot 0{,}2~м}}{0{,}016~кг}\approx 1{,}2~м/c[/math] [math]Ответ:v_{кубик}=1{,}2~м/c[/math]
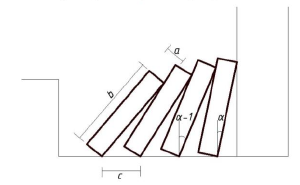
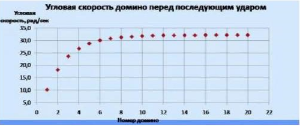
Угловая скорость домино перед последующим ударом
[math]Дано:[/math] [math]a=15~мм[/math] [math]b=75~мм[/math] [math]c=30~мм[/math] [math]M=16~г[/math] [math]m=17~г[/math] [math]v_{кубик}=1{,}2~м/c[/math] [math]Найти:~cоотношение~скоростей~домино~и~скорость~последнего~домино[/math] [math]Решение:[/math] [math]Для~нахождения~нужных~нам~величин~условимся~считать,~что~все~домино~являются~однородными~гладкими~прямоугольными~брусками.[/math] [math]Все~домино~в~начальный~момент~стоят~на~ровной~горизонтальной~плоскости.~Во~время~движения~трение~между~домино~отсутствует.[/math] [math]Проскальзывания~домино~на~поверхности~нет.[/math] [math]Тогда~для~каждой~пары~соседних~домино~выполняется~равенство:[/math] [math]sin((\alpha-1)-\alpha)=\frac{c \cdot cos\alpha}{b}-\frac{a}{b}[/math] [math]Пользуясь~этим~соотношением~можно~вычислить~углы~наклона~каждого~домино~перед~N.[/math] [math]Дифференцируя~данное~равенство,~можно~найти~соотношение~скоростей~этих~домино~в~каждый~момент~времени:[/math] [math](\alpha-1)'=(1-\frac{c \cdot sin\alpha}{b \cdot cos((\alpha-1)-\alpha)}) \cdot \alpha'[/math] [math]В~~процессе~каждое~домино~ударяет~последующее,~сообщая~ему~некоторую~начальную~скорость.[/math] [math]При~этом~согласно~эксперименту~скорость~движения~“волны”~падающих~домино~достигает~своей~постоянной~скорости~примерно~на~10~домино.[/math] [math]Поэтому~мы~можем~использовать~данное~равенство~для~нахождения~соотношения~скоростей,~так~как~в~нашем~случае~у~нас~всего~4~элемента.[/math] [math]\frac{(\alpha-1)'}{\alpha'}=1-\frac{0{,}03~м \cdot \frac{15}{75}}{0{,}075~м \cdot 0{,}97979}=0{,}9182[/math] [math]То~есть~каждая~следующая~домино~(до~10~домино)~будет~иметь~скорость,~в~\frac{1}{0{,}9182}=1{,}089~раз~большую~предыдущей.[/math] [math]Согласно~закону~сохранения~импульса(ЗСИ):[/math] [math]M \cdot v_{кубик}=m \cdot v_{1} [/math] [math]v_{1}=\frac{0{,}016~кг \cdot 1{,}2~м/c}{0{,}017~кг}=1{,}13~м/c[/math] [math]v_{4}=1{,}13~м/c \cdot (1{,}089)^3=1{,}45~м/с[/math] [math]Ответ:Соотношение~скоростей~домино~=~1{,}089.~Скорость~последнего~домино~=~1{,}45~м/c[/math]
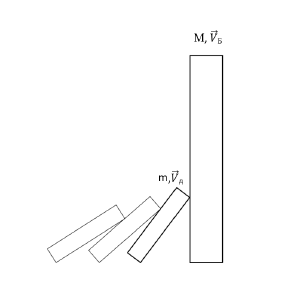
Расчёт скорости бруска, приобретенной в результате соударения
Расчет скорости бруска, приобретенной в результате соударения
[math]Дано:[/math] [math]v_{домино}=1{,}45~м/с[/math] [math]m_{домино}=0{,}017~кг[/math] [math]M_{брусок}=0{,}106~кг[/math] [math]Найти:~v_{брусок}[/math] [math]Решение:[/math] [math]Происходит~соударение~домино,~обладающего~начальной~скоростью,~с~неподвижным~бруском,~который~впоследствии~начинает~падать.[/math] [math]Воспользуемся~законом~сохранения~импульса~(ЗСИ):[/math] [math]m_{домино} \cdot v_{домино}=M_{брусок} \cdot v_{брусок} [/math] [math]v_{брусок}=\frac{m_{домино} \cdot v_{домино}}{M_{брусок}} [/math] [math]Подставим~численные~значения:[/math] [math]v_{брусок}=\frac{0{,}017~кг \cdot 1{,}45~м/c}{0{,}106~кг} [/math] [math]v_{брусок}=0{,}23~м/c [/math] [math]Ответ:v_{брусок}=0{,}23 м/c[/math]
[math]Примечание:[/math] [math]В~данной~задаче~рассматривались~идеальные~условия,~позволяющие~приближённо~рассчитать~искомую~величину.~В~реальности~при~[/math] [math]соударении~часть~механической~энергии~будет~переходить~во~внутреннюю~энергию~домино~и~бруска.~Величина,~способная~[/math] [math]охарактеризовать~данные~потери,~называется~ударной~вязкостью.[/math] [math]Ударная~вязкость~—~способность~материала~поглощать~механическую~энергию~в~процессе~деформации~и~разрушения~под~действием~[/math] [math]ударной~нагрузки.[/math] [math]В~условиях~нашей~задачи~ударная~вязкость~древесины~была~настолько~мала,~что~её~влиянием~можно~было~пренебречь~и~[/math] [math]воспользоваться~законом~сохранения~импульса.[/math]
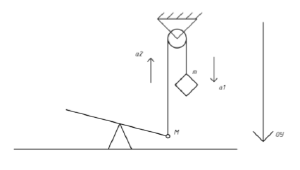
Расчёт ускорения, с которым груз, перекинутый через неподвижный блок, падает на машину
Расчет ускорения, с которым груз, перекинутый через неподвижный блок, падает на машину
[math]Дано:[/math] [math]M=0{,}054~кг[/math] [math]m=0{,}06~кг[/math] [math]g=9{,}81~м/c^2[/math] [math]Найти:~a[/math] [math]Решение:[/math] [math]По~второму~закону~Ньютона~распишем~действующие~на~грузы~силы~и~ускорение,~спроецированные~на~Oy:[/math] [math]m \cdot a_{1}=m \cdot g -T_{1}[/math] [math]-M \cdot a_{2}=M \cdot g -T_{2}[/math] [math]Нить,~перекинутая~через~блок,~нерастяжимая,~значит,~за~одно~и~то~же~время~тела~будут~проходить~одинаковые~пути.[/math] [math]Ускорения~будут~постоянны:~a_{1}=a_{2}=a.[/math] [math]Кроме~того,~масса~нити~и~блока~пренебрежимо~малы,~в~задаче~не~учитывается~момент~инерции~и~cилы~последнего.[/math] [math]Из~этого~следует,~что~сила~натяжения~нити~при~переходе~через~блок~меняет~своё~направление,~но~не~меняет~значение:[/math] [math]T_{1}=T_{2}=T[/math] [math]m \cdot a_{1}=m \cdot g -T[/math] [math]M \cdot a_{2}=T- M \cdot g[/math] [math]Решим~систему~уравнений~и~выведем~формулу~нахождения~ускорения~второго~груза:[/math] [math]T=m \cdot g - m \cdot a [/math] [math]T=M \cdot g + M \cdot a[/math] [math]m \cdot g - m \cdot a=M \cdot g + M \cdot a[/math] [math]a=\frac{m-M}{m+M} \cdot g[/math] [math]Подставив~значения~масс,~найдём~ускорение:[/math] [math]a=\frac{0{,}06~кг-0{,}054~кг}{0{,}06~кг+0{,}054~кг} \cdot 9{,}81~м/c^2=0{,}51~м/c^2[/math] [math]Ответ:а=0{,}51 м/c^2[/math]
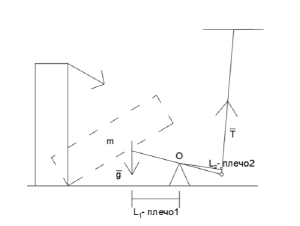
Расчёт силы натяжения нити
Расчет силы натяжения нити
[math]Дано:[/math] [math]m=0{,}106~кг[/math] [math]L_{1}=10~см[/math] [math]L_{2}=7{,}5~см[/math] [math]Найти:~T[/math] [math]Решение:[/math] [math]Используем ~закон ~сохранения ~моментов ~сил ~(ЗСМС):[/math] [math]В ~нашем ~случае: ~M_{1}=M_{2}:[/math] [math]m \cdot g \cdot L_{1}=T \cdot L_{2}[/math] [math]T=m \cdot g \cdot \frac {L_{1}}{L_{2}}[/math] [math]Подставляем ~численные ~значения ~и ~получаем ~T:[/math] [math]T=1{,}385~Н[/math] [math]Ответ:T=1{,}385~Н. [/math]
Расчёт коэффициента трения машинки с наклонной плоскостью
Расчет силы натяжения нити
[math]Дано:[/math] [math]alpha=30~deg[/math] [math]h=0{,}1~м[/math] [math]t=0{,}3~с[/math] [math]Найти:~mu[/math] [math]Решение:[/math] [math]Используя ~второй ~закон ~Ньютона:[/math] [math]m \cdot g_{U+20D7} + F_{тр}+ N= m \cdot a[/math] [math]m \cdot g \cdot L_{1}=T \cdot L_{2}[/math] [math]T=m \cdot g \cdot \frac {L_{1}}{L_{2}}[/math] [math]Подставляем ~численные ~значения ~и ~получаем ~T:[/math] [math]T=1{,}385~Н[/math] [math]Ответ:T=1{,}385~Н. [/math]
Результаты по проекту Машина Голдберга выполняет необходимую задачу: нажимает на дистанционную кнопку для создания фотоснимка. В процессе расчетов и пробных запусков были устранены некоторые этапы и модифицированы существующие конструкции. В ходе вычислений были изменены некоторые параметры установки и исправлены неполадки.
Видео рабочего процесса создания машины Голдберга.
VIDEO
Видео всех этапов Машины Голдберга.
VIDEO
Литература и ссылки Инструкция по оказанию первой доврачебной помощи
Инструкция по охране труда при работе с ручным инструментом
Как создать машину Руба Голдберга самому
Краткая теория по теоретической механике
Машина Голдберга
Методическое пособие по использованию 3D принтера DFKit
Методическое пособие по использованию ЧПУ лазерного станка DFKit
Примеры различных машин Голдберга: 75 Rube Goldberg Ideas & Inventions | DoodleChaos
The Dresser - Rube Goldberg Machine for Getting Dressed | Joseph's Machines
Marble run | Vivify cg
Мастерская Голдберга | СПб и Мск | Лекториум