Переход к тепловому равновесию в гармонической ГЦК решетке

Курсовой проект по Механике дискретных сред

Исполнитель: Ляжков Сергей

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

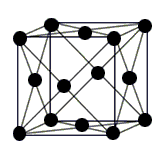
Рассмотреть поведение кинетической температуры при переходе к тепловому равновесию в бесконечной гармонической гранецентрированной кубической (ГЦК) решетке при следующих начальных условиях:

1. Частицы имеют нулевые перемещения.
2. Частицы имеют случайные скорости.
3. Распределение температуры - однородное.
4. Кинетические температуры, соответствующие различным пространственным направлениям, не равны.

Вывод уравнений

Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой [math] m [/math], соединенных линейными пружинками жесткостью [math] c [/math]. Уравнения движения частицы с радиус-вектором [math] \textbf{r} [/math] имеют следующий вид:
[math] \ddot{\textbf{u}}(\textbf{r}) = \sum_\alpha \textbf{C}_\alpha \textbf{u}(\textbf{r}+\textbf{a}_\alpha)[/math],
где [math] \textbf{u}(\textbf{r}) = (u_x, u_y, u_z)^\top [/math] - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором [math] \textbf{r} [/math], [math] \textbf{a}_\alpha [/math] - векторы, соединяющие частицу с радиус-вектором [math] \textbf{r} [/math] с ближайшими соседями. [math] \textbf{C}_\alpha [/math] - матрицы, коэффициенты которых определяют вклад частицы номер [math] \alpha [/math] в суммарную силу, действующую на частицу с радиус-вектором [math] \textbf{r} [/math]. [math] \alpha = \pm 1...\pm 6 [/math], [math] \textbf{C}_\alpha = \frac{c}{2}\textbf{n}_\alpha \textbf{n}_\alpha[/math].
Векторы [math] \textbf{n}_\alpha = \frac{\textbf{a}_\alpha}{|\textbf{a}_\alpha|}[/math] в ГЦК решетке имеют следующий вид:
[math] \textbf{n}_{\pm1}=\pm\frac{(\textbf{e}_x+\textbf{e}_y)}{\sqrt{2}}, \textbf{n}_{\pm4} = \pm(\textbf{n}_3-\textbf{n}_2) [/math]
[math] \textbf{n}_{\pm2}=\pm\frac{(\textbf{e}_y+\textbf{e}_z)}{\sqrt{2}}, \textbf{n}_{\pm5} = \pm(\textbf{n}_1-\textbf{n}_3) [/math]
[math] \textbf{n}_{\pm3}=\pm\frac{(\textbf{e}_x+\textbf{e}_z)}{\sqrt{2}}, \textbf{n}_{\pm6} = \pm(\textbf{n}_1-\textbf{n}_2) [/math],
где [math] \textbf{e}_x, \textbf{e}_y, \textbf{e}_z [/math] - орты декартового базиса, направленные вдоль осей кубической симметрии.
Сделаем следующую подстановку в уравнения движения для получения дисперсионного соотношения [math] \omega [/math]:
[math] \textbf{u}(\textbf{r}) = e^{\textrm{i}(\omega t + \textbf{k} \cdot \textbf{r})} [/math],
где [math] \textbf{k} [/math] - волновой вектор, и получим следующее уравнение:
[math] (\textbf{D}-\omega^2 \textbf{E})=0, \textbf{D} = -\frac{1}{m} \sum_\alpha \textbf{C}_\alpha e^{\textrm{i}{\textbf{k} \cdot \textbf{a}_\alpha}} [/math].
Таким образом, отыскание дисперсионного соотношения, необходимого для следующих формул, сводится к нахождению собственных чисел динамической матрицы [math] \textbf{D} [/math].
Формула для для кинетической температуры [math] T [/math]:
[math] T = \frac{T_0}{2} + B_1 + B_2 + B_3, \quad B_j = \int_\textbf{k} (\textrm{cos} (2\omega_j t)) \textrm{d} \textbf{k} [/math],
где [math] T_0 [/math] - начальное значение кинетической температуры. Величина [math] T [/math] описывает колебания температуры, связанные с выравниванием кинетической и потенциальной энергий, величины [math] B_j [/math] определяют вклад веток дисперсионного соотношения в эти колебания.
Рассмотрим бесконечное множество реализаций одного и того же кристалла. Кинетические температуры, соответствующие различным пространственным направлениям, в общем случае различаются. Следовательно, тепловое состояние описывается матричной температурой [math] \textbf{T}. [/math]
[math] k_B \textbf{T} = m \lt \dot{\textbf{u}}(\textbf{r})\dot{\textbf{u}}(\textbf{r})^\top\gt [/math],
где [math] k_B [/math] - постоянная Больцмана.
Поведение матричной температуры описывается следующей точной формулой:
[math] \textbf{T} = \int_\textbf{k} \textbf{P}\textbf{T}'\textbf{P}^\top, T'_{ij} = \frac{1}{2}(\textbf{P}^\top \textbf{T}_0 \textbf{P})_{ij}(\textrm{cos}((\omega_i+\omega_j)t)+\textrm{cos}((\omega_i-\omega_j)t)), [/math]
где [math] \textbf{P} - [/math] ортогональная матрица поляризации, составленная из единичных собственных векторов матрицы [math] \textbf{D} [/math], [math] \textbf{T}_0 [/math] - начальное значение матричной температуры.
Матричная и кинетическая температуры связаны следующим образом:
[math] T = \frac{1}{3}\textrm{tr}\textbf{T}. [/math]

Результаты

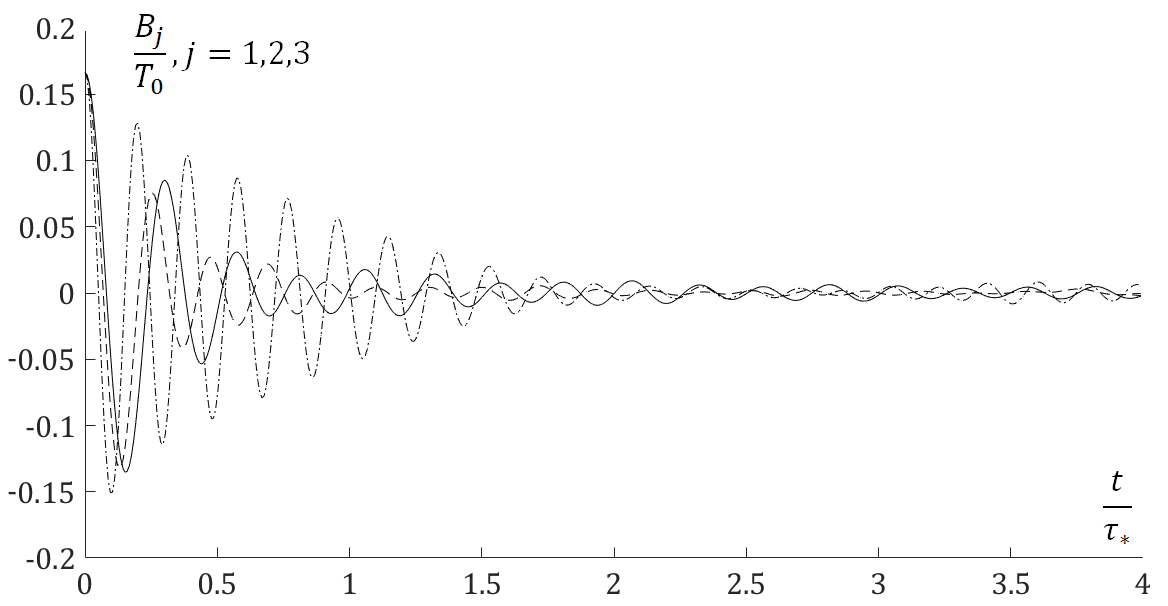
Вклады веток дисперсионного соотношения в колебания температуры:

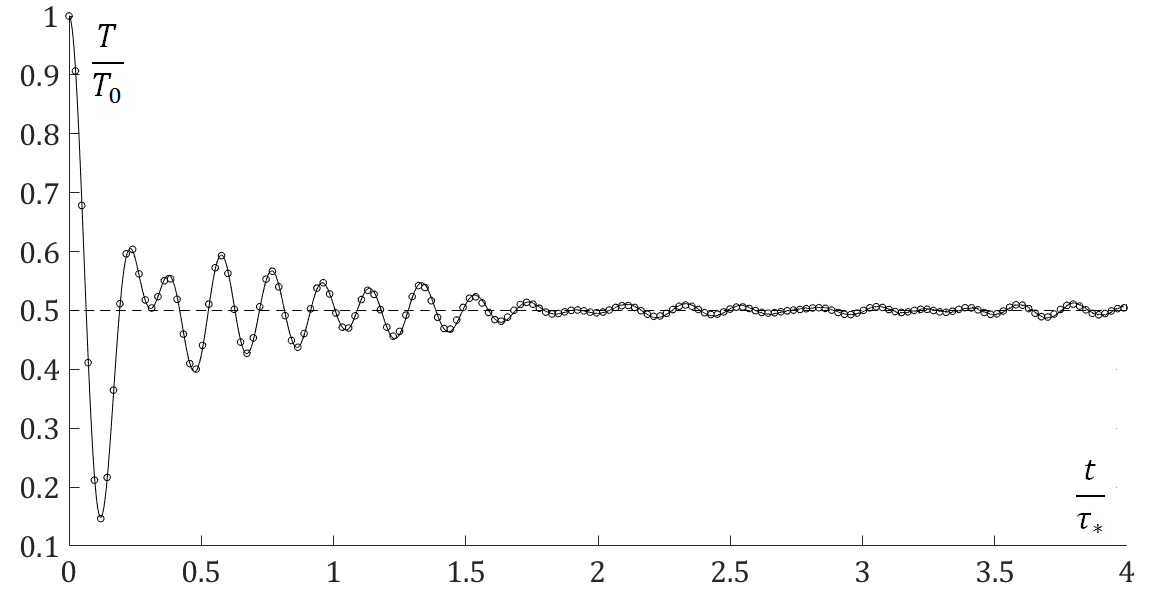
Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий:

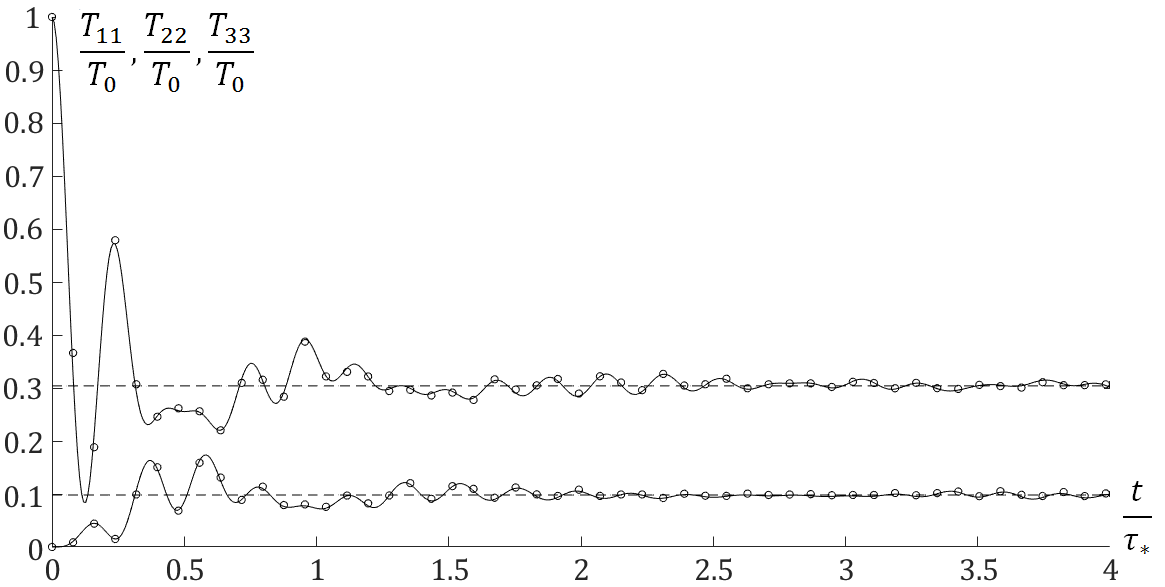
Перераспределение кинетической температуры по пространственным направлениям:

Линии - аналитическое решения по формулам, представленным в нижеприведенной статье, точки - численное решение уравнения динамики решетки.

Текст статьи

Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке

Неделя науки 2018

Данный проект был представлен на конференции "Неделя науки 2018".

Постер

См.также

Курсовые_работы_по_ВМДС:_2018-2019