Моделирование колебаний резонаторов на основе углеродных вискеров
БАКАЛАВРСКАЯ РАБОТА
Автор работы: Ванюшкина Валентина
Научный руководитель: И.Е. Беринский
Содержание
Введение
Нановискеры - структуры, полученные из аморфного углерода, длина которых не превышает сотни микрометров. Могут быть разных форм и размеров и применятся как наноинструменты. Целью данной работы является исследование динамики нановискеров с целью их оптимального применения в наноэлектромеханических системах, путем нахождения деформаций и напряжений различных наноструктур, для улучшение качеств дальнейших экспериментов, а так же подбор идеальных параметров конструкций и материалов.Это поможет значительно сократить количество неудачных экспериментов, а так же выявить новые свойства наноструктур, которые не были выявлены в ходе эксперимента. Так же с помощью данных моделирований становится более понятна природа и виды колебаний и деформаций, вызванных ими. Во всех последующих расчетах в качестве параметров материала вискеров взяты параметры аморфного углерода:Па - модуль Юнга, кг/м - плотность. При этом известно, что аморфный углерод - изотропный материал, а это значит, что его физические и механические свойства не зависят от направления.
Простейшие колебательные системы
Для представления колебаний одиночного вискера, наращенного на игле, было использовано моделирование механических систем с двумя степенями свободы. Это позволяет приближенно оценить колебания данной наносистемы и найти ее первые две собственные частоты. Задача о представлении вискера, прикрепленного к игле, была разделена на две подзадачи: о продольных колебаниях и поперечных колебаниях системы. Поскольку исследуемый объект состоит из двух тел, то логично представить его в виде системы с двумя степенями свободы. Очевидно, что в реальности степеней свободы будет бесконечное множество, но для нахождения первых двух собственных частот, достаточно рассмотреть упрощенную модель. Решения, полученные для данной задачи представленны в виде интерактивных моделей: Простейшая колебательная система с двумя степенями свободы и Колебания двойного маятника
Модель нановесов
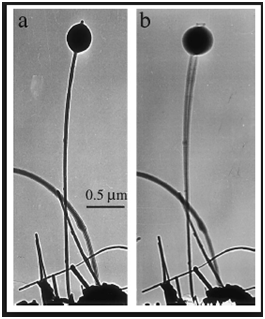
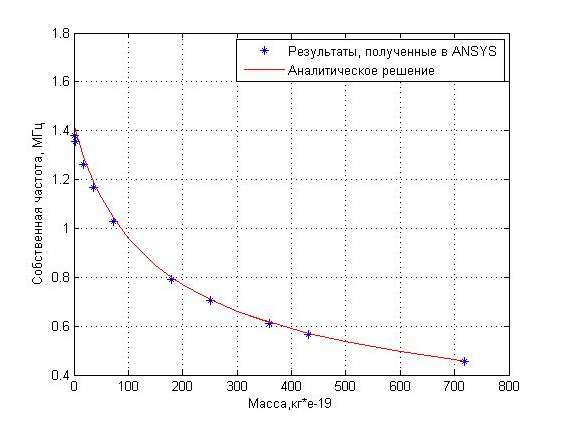
Исследуемые весы сделаны из углеродных наноструктур, называемых одиночными вискерами. Это углеродная балка очень маленьких размеров. На нее падает частица с некоторой скоростью, в результате чего вискер начинает колебаться. Исследовав колебания вискера, можно будет определить массу объекта, упавшего на вискер. Для этого была построена конечноэлементная модель вискера с точечной массой на правом конце и заделкой на левом. Проведен расчет собственных частот и форм колебаний, а так же найдено аналитическое решение:, где -собственная частота колебаний системы.
Было проведено сравнение результатов, полученных аналитически и методом конечных элементов.
Конечноэлементное моделирование сложных структур.
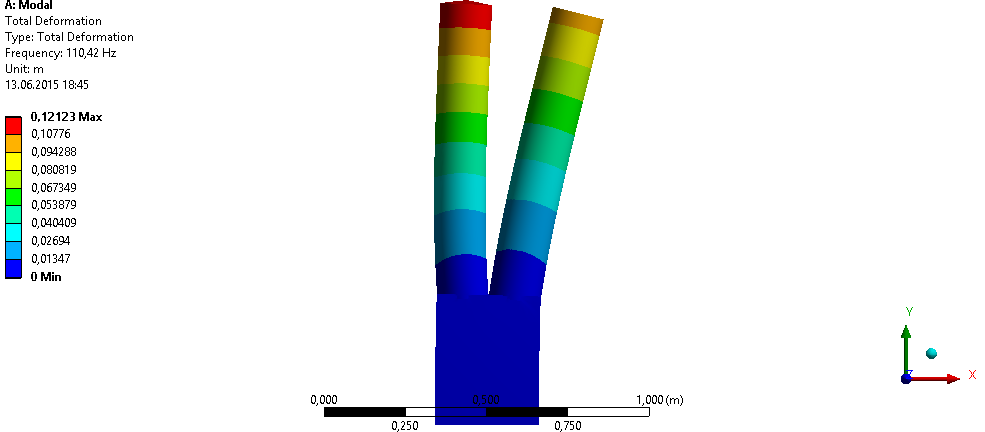
Для рассмотрения колебаний сложных структур, были созданы их конечноэлементные мо- дели и проведен расчет собственных и вынужденных колебаний.При создании моделей, бы- ли использованы размеры реальных наноконструкций, но увеличенные в 106 раз, так как в программном пакете ANSYS Workbench не предусмотрена работа с наноразмерами, однако понятно, что собственные формы не изменятся, а значения частот уменьшатся в 106 раз, не меняя при этом свое мантиссы. Некоторые из получившихся результатов представлены ниже.
Выводы
В данной работе проведено исследование продольных и поперечных колебаний вискера на игле с помощью представления этой системы в виде механической системы с двумя степенями свободы. Для продольных и поперечных колебаний были найдены аналитически уравнения движения и созданы интерактивные модели.Эти модели позволяют анализировать текущее движение системы в зависимости от параметров вискера и иглы.
В дальнейшем к данной части работы будет добавлена модель с постоянным гармоническим воздействием на иглу, что позволит исследовать колебания, более приближенные к реальным и рассмотреть случай динамического гашения колебаний вискера.
Так же была рассмотрена модель нановесов для случая падения массы точно на конец вискера.
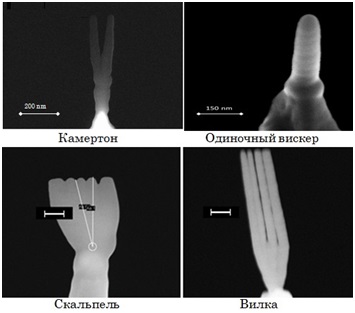
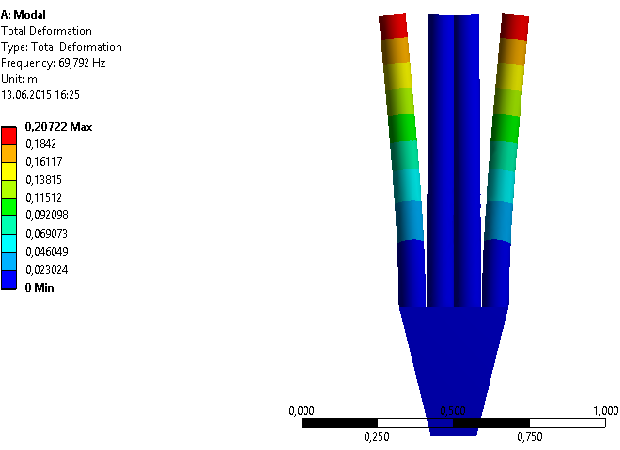
Были смоделированы сложные конструкции из вискеров, такие как вилка, скальпель и камертон. При моделировании этих конструкции мы получили два набора собственных частот (два спектра), так как модели трехмерные. Полезны собственные частоты и формы только в плоскости самой конструкции, так как при реальных экспериментах колебания происходят именно в этих плоскостях. Найдены только первые две собственные частоты каждого спектра, это объясняется тем, что чем ниже порядок частоты, тем проще попасть в нее при реальных экспериментах. Практически невозможно попасть в резонанс с третей и выше собственными частотами.
Для модели вискера на игле представлены только две собственные формы, так как эта модель осесимметрична и ее спектры и собственные формы, соответствующие частотам этих двух спектров совпадают,но располагаются в разных плоскостях. В дальнейшем, планируется решить полностью задачу нановесов, составив систему уравнений, для нахождения собственных частот; исследовать более сложные конструкции, например трехмерные; создать интерактивную модель динамического гасителя колебаний.
Продолжение данного исследования необходимо, так как направление экспериментального создания вискеров развивается очень быстро. За последний год были построены и исследова- ны гораздо более сложные конструкции и найдены новые пути их применения. Но каждый эксперимент трудоемок, сложен и требует как финансовых, так и ресурсных затрат. В будущем планируется предсказывать результаты эксперементов с целью сокращения их числа и достижения максимальной эффективности работы специалистов-экспериментаторов.
Список литературы
- Z.L.Wang, P.Poncharal, W.A. de Heer. Measuring physical and mechanical properties of individual carbon nanotubes by in situ TEM. J. Phys. Chem. Solids, 2000, 61(7), pp.1025- 1030
- Dynamik der Baukonstruktionen, Christian Petersen 2000 1st edition,722 [3] И.М.Бабаков. Теория колебаний.1968,3
- Я.С.Гринберг, Ю.А.Пашкин, Е.В.Ильичев. Наномеханические резонаторы.2012.
- Mai Duc Dai, Chang-Wan Kim, Kilho Eom. Nonlinear vibration of graphene resonators and their applications in sensitive mass detection. Nanoscale Research Letters 2012 7:499
- Новопашенный Г.Н. Электронные измерительные приборы. 1966. 268