КП: Эффект Магнуса

А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Эффект Магнуса

---

Курсовой проект по Теоретической механике

Исполнитель: Шварёв Николай

Группа: 09 (23604)

Семестр: весна 2015

Сила Магнуса

Аннотация проекта

Данный проект посвящен изучению эффекта Магнуса, возникающего в различных видах спорта, а также использующегося в баллистике, летательных аппаратах и кораблях.В ходе работы над проектом были рассмотрены траектории полета мяча в зависимости от различных начальных параметров (радиуса мяча, динамической вязкости среды, плотности воздуха, линейной и угловой скорости мяча). Программа написана на языке JavaScript с использование библиотеки Three.js.

Формулировка задачи

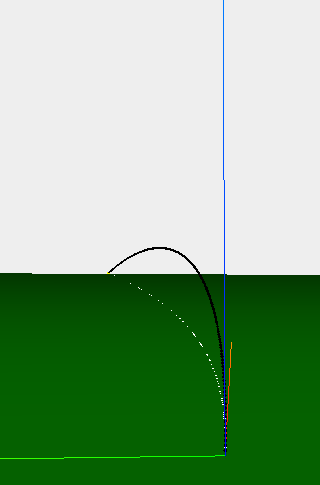
Построение и исследование математической модели движения объекта (в нашем случае - футбольного мяча), получение уравнения его движения и построение траектории в трехмерном пространстве с учётом различных внешних факторов, влияющих на движение, таких как сила сопротивления воздуха и эффект Магнуса.

Общие сведения по теме

Пример влияния силы Магнуса на траекторию движения мяча

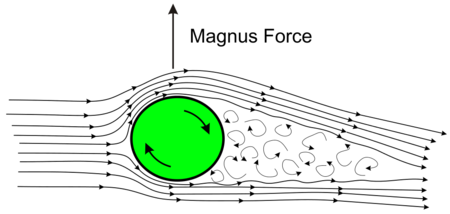
Эффект Магнуса - образование подъемной силы, действующей на вращающееся тело при обтекании его потоком жидкости или газа, широко использующейся в спорте, баллистике, летательных аппаратах и кораблях.

Данный эффект возникает в результате разности давлений (в соответствии с законом Бернулли) на стенках мяча из-за разных скоростей движения воздуха. Возникающий дисбаланс заставляет мяч отклоняться.

Решение

Силу сопротивления воздуха будем считать с помощью закона Стокса:

[math]\vec{F} = -6πrη\vec{v} [/math] , где

[math]\vec{F}[/math] - сила Стокса,

[math]r[/math] - радиус мяча,

[math]η[/math] - динамическая вязкость среды,

[math]\vec{v}[/math] - скорость мяча.

Силу Магнуса примем вида:

[math]\vec{F} = 8πρr^3\vec{u}\times\vec{ω} [/math] , где

[math]\vec{F}[/math] - сила Магнуса,

[math]ρ[/math] - плотность воздуха,

[math]r[/math] - радиус мяча,

[math]\vec{u}[/math] - относительная скорость мяча,

[math]\vec{ω}[/math] - угловая скорость мяча.

Применив метод Эйлера, получим формулы для нахождения скорости и координаты мяча:

[math] \begin{cases} v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 8πρr^3(u_y^iω_z - u_z^iω_y)/m)\Delta t \\ v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 8πρr^3(u_z^iω_w - u_x^iω_z)/m)\Delta t \\ v_z^{i+1} = v_z^i + (-6πrηv_z^i/m - g + 8πρr^3(u_x^iω_y - u_y^iω_x)/m)\Delta t \\ \end{cases} [/math]

[math] \begin{cases} x^{i+1} = x^i + v_x^i\Delta t \\ y^{i+1} = y^i + v_y^i\Delta t \\ z^{i+1} = z^i + v_z^i\Delta t \\ \end{cases} [/math]

Реализация алгоритма:

Обсуждение результатов и выводы

Пример траектории мяча

Разработанный алгоритм был реализован в среде программирования Javascript с использование библиотеки Three.js. Была построена траектория движения и произведены эксперименты, результаты которых находятся в таблице ниже:

[math]V_x[/math]	[math]V_y[/math]	[math]V_z[/math]	[math]ω_x[/math]	[math]ω_y[/math]	[math]ω_z[/math]	[math]Δ_y[/math]	[math]ω_x[/math]	[math]ω_y[/math]	[math]ω_z[/math]	[math]Δ_y[/math]	[math]ω_x[/math]	[math]ω_y[/math]	[math]ω_z[/math]	[math]Δ_y[/math]	[math]ω_x[/math]	[math]ω_y[/math]	[math]ω_z[/math]	[math]Δ_y[/math]
5	0	5	0	0	-5	2.4644	5	0	-5	3.2022	0	0	-10	4.8584	5	0	-10	5.4070
10	0	5	0	0	-5	4.9289	5	0	-5	5.4903	0	0	-10	9.9168	5	0	-10	9.6552
15	0	5	0	0	-5	7.3934	5	0	-5	7.6860	0	0	-10	14.5751	5	0	-10	13.6855
20	0	5	0	0	-5	9.8578	5	0	-5	9.7909	0	0	-10	19.4335	5	0	-10	17.4784

где [math]V_x[/math], [math]V_y[/math], [math]V_z[/math] - начальные линейные скорости, [math]ω_x[/math], [math]ω_y[/math], [math]ω_z[/math] - начальные угловые скорости, а [math]Δ_y[/math] - полученное смещение по оси [math]y[/math].

Скачать отчет:
Скачать презентацию:

См. также

• Справочная информация
• Курсовые проекты ТМ