Моделирование гидроразрыва пласта
Содержание
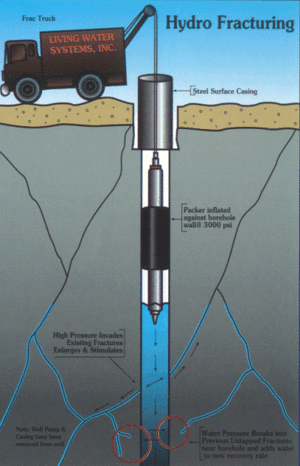
Гидравлический разрыв пласта
Гидроразры́в пласта́ (ГРП) — один из методов интенсификации работы нефтяных и газовых скважин и увеличения приёмистости нагнетательных скважин. Метод заключается в создании высокопроводимой трещины в целевом пласте для обеспечения притока добываемого флюида (газ, вода, конденсат, нефть либо их смесь) к забою скважины. Технология осуществления ГРП включает в себя закачку в скважину с помощью мощных насосных станций жидкости разрыва (гель, в некоторых случаях вода, либо кислота при кислотных ГРП) при давлениях выше давления разрыва нефтеносного пласта. Для поддержания трещины в открытом состоянии в терригенных коллекторах используется расклинивающий агент — проппант, в карбонатных — кислота, которая разъедает стенки созданной трещины.
A ‘‘typical’’ hydraulic fracturing treatment starts with the creation of an initial path for the fracture. This is usually achieved by a technique called ‘‘perforation’’ in which specially designed shaped-charges are blasted on the wellbore walls with given orientations, perforating the casing and creating finger-like holes or weak points in the hydrocarbon-laden formation. A viscous fluid is pumped inside the wellbore, inducing a steep rise in the pressure which eventually leads to the initiation of a fracture at the perforated interval. A ‘‘pad’’ of clean fluid is usually pumped first, to provide sufficient fracture width for the proppant that follows. Proppant is injected at a later stage as a suspension or slurry. The treatment usually takes place on a time-scale of tens of minutes to a few hours, depending upon the designed fracture size and volume of proppant to be placed. At the end of the treatment, when pumping stops, leak-off of the residual fracturing fluid into the porous reservoir allows the fracture surfaces to close onto the proppant pack under the action of the far-field compressive stresses.
Физические процессы, сопровождающие гидроразрыв
Основные процессы:
- деформирование и разрушение горной породы под действием жидкости
- течение жидкости в трещинах гидроразрыва
- транспорт проппанта в трещинах гидроразрыва
Особенности "реального" процесса гидроразрыва:
- неоднорподность (в частности, слоистая структура) горной породы;
- changes in magnitude and/or orientation of the in situ confining stresses;
- пристствие свободных порехностей;
- утечка жидкости, используемой для гидроразрыва, в горную породу либо наоборот приток жидкости в трещины из породы;
- влияние температуры и сдвига на реологические свойства разрушающей жидкости;
- закрытие трещин в следствие прекращения накачки жидкости, намеренной откачки жидкости или резкого изменения геометрии за счет образования трещин (разгрузка породы);
- гидроразрыв так называемых ‘‘мягких’’ пород, таких как слабо консолидированны such as weakly consolidated песчанник. Линейная механика разрушения к ним не применима!
Методы, используемые в литературе
Для моделирования разрушения горной породы в процессе гидроразрыва используются как методы механики сплошной среды (метод конечных элементов, метод граничных элементов), так и механики дискретных сред (метод дискретных элементов).
Континуальные подходы к моделированию гидроразрыва
Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 В статье дается обзор континуальных подходов к моделированию гидроразрыва. В частности, отмечается, что при использовании континуальных методов, как правило, вводятся следующие ограничения:
- материал резервуара (горной породы) считается линейно упругим;
- в случае слоистого резервуара слои считаются параллельными и идеально сопряженными;
- гидроразрыв происходит в одной вертикальной плоскости плоскости;
- usually, the fluid flow equations are restricted to relatively simple models for the fluid rheology, such as Newtonian or power-law. However, actual fluids used for hydraulic fracturing treatments have more complicated rheologies (yield stresses, viscoelasticity, etc.);
- the fluid flow in the fracture obeys Poiseuille flow and is incompressible, sequential injections of multiple fluids are immiscible.
- leak-off is often assumed to be uncoupled from the fluid pressure, and to be restricted to the linear (1D) flow regime;
Как правило, не учитывается:
- неупругое (пластическое) поведение породы;
- непараллельность и неидеальная сопряженность поверхностей слоев;
- реальная геометрия трещины;
- естественная трещиноватость породы;
- начальные неоднородные поля напряжений, вызванные, в частности, пористостью структуры.
Olson J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands // 42nd US Rock Mechanics Symposium, 2008
The diagnostic data suggests that in some situations, complex, multistranded fracture zones or networks develop as a result of interaction between the hydraulic fracture and pre-existing natural fractures. This paper examines complex hydraulic fracture pattern development using techniques previously applied to the analysis of natural fracture network development and the fracture of silicon wafers in microchip manufacture. The numerical code is based on a pseudo-3d displacement discontinuity solution, where the propagation of hundreds of fracture tips can be tracked simultaneously, with propagation velocities proportional to the stress intensity factor at each crack tip. The method does not yet solve for flow through the hydraulic fracture network, but instead uses a simplified constant pressure boundary condition for all fracture segments connected to the wellbore, enabling a preliminary analysis of this complex problem.
Lin J., Zhu D. Predicting well performance in complex fracture systems by slab source method // SPE Hydraulic fracturing conference, 2012.
The model for the flow inside fracture pattern is proposed.
Fu P., Johnson S.M., Hao Y., Carrigan C.R. Fully coupled geomechanics and discrete flow network modeling of hydraulic fracturing for geothermal applications // Proc. of 36 Workshop on Geothermal Reservoir Engineering
The primary objective of our current research is to develop a computational test bed for evaluating borehole techniques to enhance fluid flow and heat transfer in enhanced geothermal systems (EGS). Simulating processes resulting in hydraulic fracturing and/or the remobilization of existing fractures, especially the interaction between propagating fractures and existing fractures, represents a critical goal of our project. To this end, we are continuing to develop a hydraulic fracturing simulation capability within the Livermore Distinct Element Code (LDEC), a combined FEM/DEM analysis code with explicit solid-fluid mechanics coupling. LDEC simulations start from an initial fracture distribution which can be stochastically generated or upscaled from the statistics of an actual fracture distribution. During the hydraulic stimulation process, LDEC tracks the propagation of fractures and other modifications to the fracture system. The output is transferred to the Non-isothermal Unsaturated Flow and Transport (NUFT) code to capture heat transfer and flow at the reservoir scale.
Дискретные подходы к моделированию гидроразрыва
Torres S.A.G., Castaño J.D.M. Simulation of the hydraulic fracture process in two dimensions using a discrete element method// Phys. Rev. E 75, 066109, 2007.
We introduce a discrete element simulation for the hydraulic fracture process in a petroleum well which takes into account the elastic behavior of the rock and the Mohr-Coulomb fracture criteria. The rock is modeled as an array of Voronoi polygons joined by elastic beams, which are submitted to tectonical stresses and the hydrostatic pressure of the fracturing fluid. The fluid pressure is treated like that of a hydraulic column. We also include an analysis of the fracturing fluid loss due to the permeability of the rock which is useful in an efficiency analysis of the treatment.
S. Deng, R. Podgorney, H. Huang, Discrete Element Modeling of rock deformation, fracture network development, permeability evolution under hydraulic stimulation // Proc. 36 Workshop on Geothermal reservoir engineering, 2011.
- 3D discrete element method with bonded particle model (BPM)
- two way coupling with fluid dynamics (model for network fluid flow)
J.P. Pruiksma, A. Bezuijen Hydraulic fracturing with distinct element method // Report of DELFRAC consortium, 2002
In this report, hydraulic fracturing is investigated using the distinct element code PFC2D from Itasca. Special routines adding fluid flow to PFC2D and updating the fluid flow domains when fractures appear. After the set-up of the hydraulic fracturing simulations has been discussed, with all the main input parameters, several main parameters are varied to study the resulting fracture patterns, pressure distributions and borehole pressures. These parameter studies are: particle size dependency of the simulations, behaviour at various confining stresses, the influence of the internal friction angle of the sand and the fracturing behaviour for different borehole injection rates. After this parameter study, comparisons are made with experiments done at TU Delft, GeoDelft and in the literature. The simulation results show the same trends as the experiments and are also in good agreement quantitatively.
- 2D discrete element method with bonded particle model (BPM)
H. Shimizu, T.Koyama, S. Murata, T. Ishida, M. Chijimatsu, T. Fujita, S. Nakama Distinct element modeling for Class II behavior of rock and hydraulic fracturing // International Journal of the JCRM vol.7, 2011, pp.33-36.
Newly developed numerical approaches using the Distinct Element Method (DEM) were presented, and a series of DEM simulations were performed for better understanding the physical phenomena and mechanism for the following two fundamental issues in rock engineering field. The first issue is the Class II behavior of the brittle rocks under uniaxial compression. The radial strain control method for uniaxial compression tests was introduced in the DEM codes and the Class II behavior of rocks was simulated. The simulation results suggest that the DEM can reproduce the Class II behavior of the rock successfully and revealed that the loading condition of rocks (radial strain control) will play an important role for the Class II behavior. The second issue is the hydraulic fracturing behavior in rocks. A series of simulations for hydraulic fracturing in rock was performed by using the flow-coupled DEM code. Simulation results clearly show that the fluid infiltration behavior depends on the fluid viscosity.
- 2D discrete element method with bonded particle model (BPM)
Park N. DE modeling of rock fracture behavior: fracture toughness and time-dependent fracture growth // PhD thesis, 2006.
- 3D discrete element method with bonded particle model (BPM)
- Cundal's model for fluid flow is used (unpublished)
Wu R. Some Fundamental Mechanisms of Hydraulic Fracturing, PhD thesis, 2006
- 2D discrete element method with bonded particle model (BPM)
- Cundal's model for fluid flow is described
Моделирование динамики проппанта
The transport and placement of proppant within the fracture is usually modeled by representing the slurry (i.e., the mixture of proppant and fluid) as a two-component, interpenetrating continuum. The distribution of proppant in the fracture is given by its volumetric concentration (defined as the probability of finding a proppant particle at a given point in space and time), which is the additional variable to be determined. In modeling proppant transport and placement, it is often assumed that:
- both proppant and fluid are incompressible;
- the proppant particles are small compared to a characteristic lengthscale, in this case the fracture width;
- the only mechanism to account for ‘‘slip’’ between the proppant and the carrying fluid is gravity-induced settling, i.e., relative proppant-fluid velocities due to migration by self-diffusion (created by shearing and/or proppant collision), Taylor dispersion, or clustering are usually neglected. This implies that, in the absence of gravity, the proppant and fluid move at the same velocity at any given point.
- interaction and collision between proppant particles, shearinduced proppant migration, proppant settling, etc.
Литература
1. Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 (download, pdf)