Проект "Фехтование"

Цели проекта

• Создание модели руки фехтовальщика
• Высокоскоростная съемка и анализ фехтовальных движений

Над проектом работают

• Дзенушко Дайнис
  
• Фролова Ксения
  
• Александров Сергей
  

Научный руководитель: Е.А. Иванова

План

1. Создать модель которая по заданным параметрам (углам в суставах, координатам плеча) восстанавливает положение руки и приходит в него из любого положения (с визуализацией)
2. Определить ограничения движения руки в суставах
3. Снять технику фехтования на высокоскоростную камеру
4. Проанализировать технику и выявить набор простейших движений из которых состоят удары
5. Найти параметры элементарных движений от которых зависит то куда придется удар
6. Обучить модель простейшим движениям
7. Создать базу ударов и обучить им модель
8. Используя параметры выявленные в пункте 4 обучить модель по заданному конечному положению руки и виду удара проводить этот удар

Поэтапное решение задачи

Постановка задач, решаемых в реальном времени:

задача	сроки выполнения
аналитическое описание простейшего действия - движения руки вперед из положения "согнута в локте" в положение "выпрямлена".Нахождение отношений угловых скоростей в суставах;	06.03.2012 - 13.03.2012

Что мы хотим получить

Модель руки которая по заданным конечным параметрам руки и виду удара воспроизводит этот удар

Восстановление положения руки по заданным параметрам

Степени свободы

Наша модель руки имеет 9 степеней свободы:
2 - поступательное движение плеча (вперед/назад;вверх/вниз)
3 - плечевой сустав (сферический шарнир)
1 - локтевой сустав
1 - вращение кистью вокруг своей оси
2 - запястье (2 перпендикулярных цилиндрических шарнира)

Поворот руки

В нашем случае рука состоит из трех частей представленных тремя векторами:

1. Плечевая кость соответствует [math]\b{a}[/math]
2. Локтевая кость соответствует [math]\b{b}[/math]
3. Кисть соответствует [math]\b{c}[/math]

С ними связаны базисы base1; base2; base3 соответственно.
Изначальное положение руки - вытянутая горизонтально в право (правая рука), ось поворота локтя вертикальна
Повороты частей осуществляются посредством поворота соответствующего вектора вокруг определенной оси. Это достигается посредством скалярного умножения вектора слева на тензор поворота, который рассчитывается следующим образом
[math]\b{\b{P}}(\phi,e) = \b{e}\b{e} + (\b{\b{E}} - \b{e}\b{e})cos(\phi) + \b{e} \times \b{\b{E}}sin(\phi)[/math]
[math]\widetilde{\b{a}} = \b{\b{P}}(\xi,\widetilde{\widetilde{\b{k})}} \cdot\b{\b{P}}(\psi,\widetilde{\b{j})} \cdot\b{\b{P}}(\varphi,\b{i}) \cdot \b{a}[/math]
После этого необходимо также повернуть остальные (отстоящие еще дальше от плеча чем рассматриваемый) векторы и соответствующие им базисы также умножив их слева на тот же тензор поворота [math]\b{\b{P}}(\phi,e)[/math]
Таким образом осуществляется поворот всех 3х векторов на необходимые углы. Затем вычисляем координаты суставов:
[math]\b{o}[/math] - радиус-вектор плеча
локоть - [math]\b{r} = \b{o}+\b{a}[/math]
запястье - [math]\b{r} = \b{o}+\b{a}+\b{b}[/math]
кончик кисти - [math]\b{r} = \b{o}+\b{a}+\b{b}+\b{c}[/math]

Вращение

Визуализация движения подразумевает нахождение траектории движения. Здесь мы встретили проблему: необходимо разбить весь поворот на малые, последовательное применение которых в конечном итоге и приведет руку в заданное положение и при этом мы получим траекторию движения. Если мы просто разделим углы на количество шагов и будем каждый раз поворачивать руку на эти малые углы то в случае когда каждый сустав вращается вокруг только одной оси все будет хорошо, но в случае поворота вокруг двух и более осей вместе с поворотом вектора также будет вращаться и связанный с ним базис в результате каждый следующий малый поворот будет осуществляться вокруг уже немного повернутых осей и мы придем уже в другое положение чем если мы один раз применим тензор поворота с полными углами. Эта проблема сейчас и решается.

Реализация поворота в пакете MATLAB

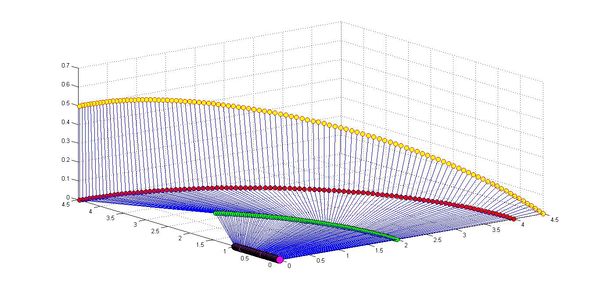
Используя пакет MATLAB был реализован данный алгоритм поворота с целью построить траекторию движения руки и проверить правильность алгоритма. Все вполне правдоподобно выглядит.
Пример движения руки:

• 



См. также

• Высокоскоростная видеокамера
• Научные работы студентов