Колебания одномерной цепочки — различия между версиями
Loban9614 (обсуждение | вклад) (→Анализ результатов) |
Loban9614 (обсуждение | вклад) |
||
| Строка 41: | Строка 41: | ||
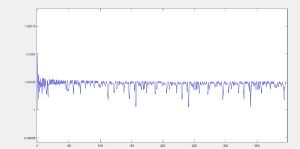
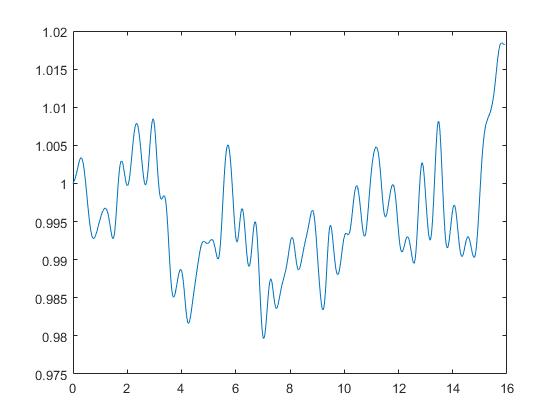
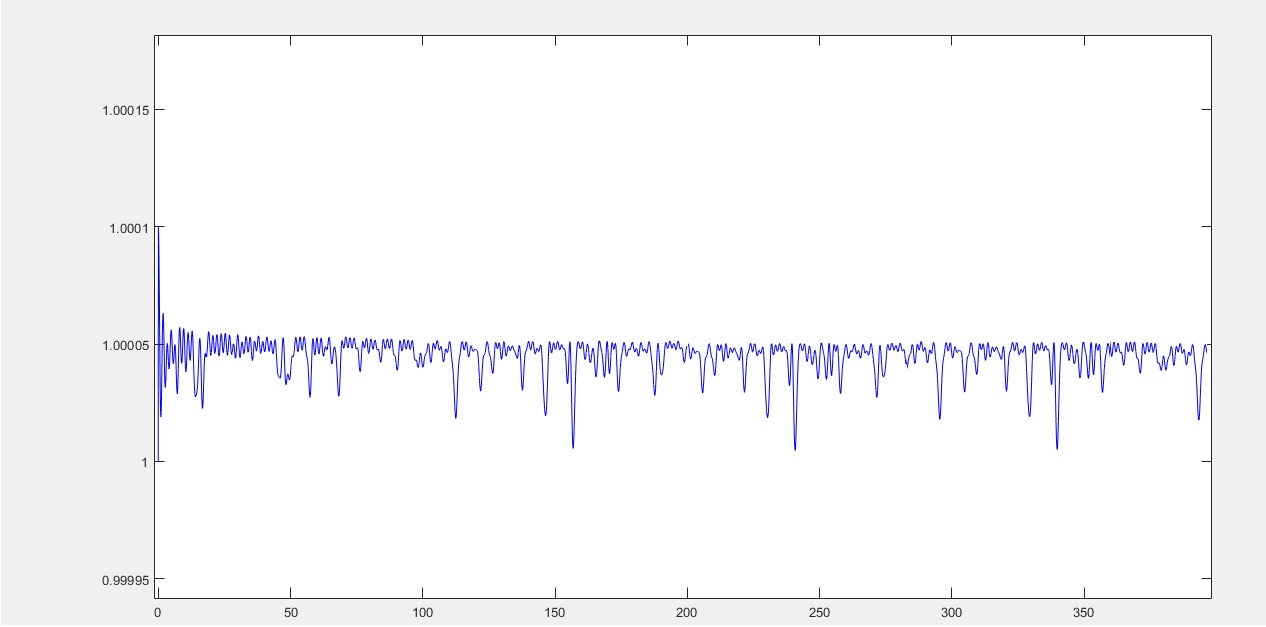
| − | [[File:energy12.jpg| | + | [[File:energy12.jpg|framed|center|График изменения энергии в системе]] |
Версия 03:45, 28 января 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Лобанов Илья
Группа: 43604/1
Постановка задачи
Рассматривается цепочка из N материальных частиц P0, P1, ... Pn, ..., PN–1, каждая из которых обладает одинаковой массой m. Частицы соединены линейными пружинками. Рассматриваются продольные колебания образующих цепочку частиц под действием сил взаимодействия между частицами цепочки, а также параллельных направлению цепочки внешних сил. Уравнение движения имеет вид:
где С - жёсткость одной пружинки, m - масса одной частицы, - перемещение частицы, a - расстояние между двумя соседними частицами в начальный момент времени.
Период одного колебания:
Движение частицы с номером n описывается зависимостью от времени t её смещения Un относительно положения равновесия этой частицы (узла цепочки с номером n).Взаимодействие задаётся с помощью потенциала Леннарда-Джонса
Решение задачи
Рассмотрим модель колебаний одномерной многоатомной цепочки равных масс. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома un, а атома, отстоящего от него на p узлов, – un+p. Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево.
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой, соответствующей потенциалу Леннарда-Джонса с коэффициентом упругости С.
Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. В соответствии с элементарным законом Гука эту силу можно представить в виде:
В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.
Для решения данного дифференциального уравнения использовали метод Верле
Анализ результатов
'