Моделирование распространения тепла в треугольной кристаллической решетке — различия между версиями
Alena dav (обсуждение | вклад) (→Описание алгоритма) |
Alena dav (обсуждение | вклад) (→Описание алгоритма) |
||
| Строка 31: | Строка 31: | ||
Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца) | Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца) | ||
::<math> | ::<math> | ||
| − | V_0 = random(-K sqrt{T(x); K sqrt{T(x)}} | + | V_0 = random(-K \sqrt{T(x); K \sqrt{T(x)}} |
</math>. Положение всех точек в начальный момент времени соответствует равновесному положению. Такие начальные условия не являются реалистичными, поскольку вся энергия системы является кинетической. Но, как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем. | </math>. Положение всех точек в начальный момент времени соответствует равновесному положению. Такие начальные условия не являются реалистичными, поскольку вся энергия системы является кинетической. Но, как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем. | ||
# Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы | # Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы | ||
::<math> | ::<math> | ||
| − | \ddot{u} = \frac{c}{m}(u_{i+1,j+1}+u_{i+1,j-1}+u_{i+1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i-1,j} - 6 u_{i,j}); j =2n | + | \ddot{u} = \frac{c}{m}(u_{i+1,j+1}+u_{i+1,j-1}+u_{i+1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i-1,j} - 6 u_{i,j});\text{ } j =2n |
</math> | </math> | ||
::<math> | ::<math> | ||
| − | \ddot{u} = \frac{c}{m}(u_{i-1,j+1}+u_{i-1,j-1}+u_{i-1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i+1,j} - 6 u_{i,j}); | + | \ddot{u} = \frac{c}{m}(u_{i-1,j+1}+u_{i-1,j-1}+u_{i-1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i+1,j} - 6 u_{i,j});\text{ } j =2n+1 |
</math> | </math> | ||
# Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям. | # Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям. | ||
Версия 12:18, 24 января 2019
Содержание
Постановка Задачи
Исследовать процесс распространения тепла в бесконечной треугольной скалярной кристаллической решетке. Сформулировать и поставить численный эксперимент, который будет наиболее точно соответствовать теоретической задаче.
Кристаллическая решетка
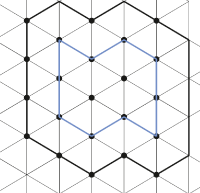
Рассматривается плоская кристаллическая скалярная решетка. Атомы этой решетки расположены в вершинах равных правильных треугольников и имеют одинаковую массу m. Связи между атомами моделируются линейными пружинками с жесткостью k. Каждый атом имеет одну степень свободы - он может двигаться вдоль прямой, перпендикулярной плоскости решетки. Схематически решетка представлена на рисунке 1.
Процесс распространения тепловой энергии в кристалле проходит на молекулярном уровне, как следствие материалы с правильной регулярной структурой могут обладать особыми свойствами теплопроводности, которые могут зависеть от направления. Для исследования свойств теплопроводности в каком-то одном из направлений необходимо смоделировать бесконечную плоскую решетку, задать температуру вдоль выделенного направления (при этом во всех точках, лежащих на одной прямой, перпендикулярной выделенному направлению температура будет одинаковой) и наблюдать за скоростью, с которой тепловая энергия будет распределяться в кристалле. Чем быстрее температура выравнивается, тем больше теплопроводность кристалла в данном направлении.
Периодичные начальные условия
К сожалению, расчет бесконечной решетки (и как следствие бесконечного числа частиц) потребовал бы бесконечных вычислительных мощностей или бесконечного времени на расчет. Если ограничиться достаточно большой решеткой, но конечных размеров, это приведет к ухудшению точности в связи с влиянием эффектов на границе и потребует значительных ресурсов при вычислениях. Из этой ситуации позволяет выйти периодичность кристаллической решетки. Если задать начальное одномерное распределение температуры, которое можно задать также периодичным. Таким образом мы получаем, что всю бесконечную плоскость можно разбить на конечные участки, на каждом из которых будут одинаковые начальные условия и одинаковая геометрия решетки. Это позволяет заменить задачу про бесконечную плоскость на задачу о конечном участке с периодичными граничными условиями. В качестве периодичной функции температуры вдоль выделенного направления использован синус. Распределение температуры в пространстве задавалось законом:
в первом случае и
где x,y - декартовы координаты в плоскости решетки
Периодические граничные условия
Бесконечную плоскость треугольной кристаллической решетки можно разбивать на фигуры различных форм и размеров. Но наиболее простыми и оптимальными вариантами являются шестиугольники и прямоугольники (конечно, две из сторон такого прямоугольника не будут прямыми из-за геометрии решетки). Поскольку начальные условия задачи имеют одно выделенное направление, то единственным подходящим вариантов ячейки периодичности решетки является прямоугольник.
Синим контуром обведены частицы, которые являются уникальными (не повторяющимися), а черным контуром – частицы, данные о которых хранятся и обрабатываются в программе. Размеры решетки, используемой для расчетов много больше представленных на рисунке и составляют порядка сотни частиц.
Описание алгоритма
В данной программе решается задача для двух направлений – вдоль одного из направлений связей и перпендикулярно ему. Основные этапы расчета содержат:
- Создание начальной конфигурации решетки, массива температур. Для каждого ряда (или столбца) высчитывается его температура по формуле
Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца)
- . Положение всех точек в начальный момент времени соответствует равновесному положению. Такие начальные условия не являются реалистичными, поскольку вся энергия системы является кинетической. Но, как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем.
- Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы
- Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям.
- Вычисление амплитуды. Этот этап необходим непосредственно для определения теплопроводности в данном направлении. Амплитуда высчитывается как скалярное произведение температуры в данный момент времени и синуса той же частоты, что и в начальных условиях (интегрирование по периоду).
Результаты
В результате численного эксперимента были получены следующий графики:
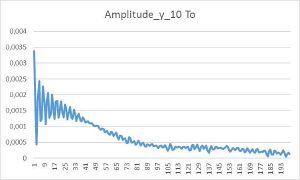
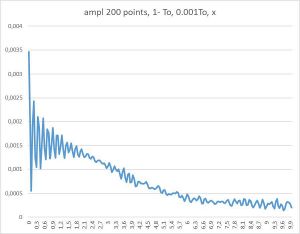
- График зависимости амплитуды от времени при T_max = 10 T0, dt = 0.001 T0, ось вдоль связей, 200 точек.
- График зависимости амплитуды от времени при T_max = 10 T0, dt = 0.001 T0, ось перпендикулярна одному из направлений связей, 200 точек.
В результате анализа графиков было получено, что тепло распространяется в двух исследуемых направлениях одинаково, при том, что геометрия решетки не является симметричной относительно поворота на 90 градусов. Возможно, из этого эксперимента следует, что теплопроводность треугольной решетки вообще во всех направлениях одинакова.(но это не точно)
Ссылки
- Курсовые_работы_по_ВМДС:_2018-2019
- Автор работы - Давыдова Алена
- Руководитель - Виталий Андреевич Кузькин